Критерий Пирсона

Разбиваем полученные в опытах значения Tна kинтервалов:

k – число интервалов. Выдвигаем гипотезу Hо том, что выбранная теоретическая плотность вероятной случайной величины T есть функцияf(t).

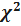В качестве величины выбираем величину , определяемую по формуле

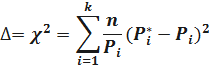
гдеn – число опытов (число отказов);

– частота попадания случайной величины Tв интервал ;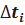

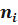– количество значений случайной величины T, попавших в интервал ;

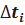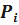– вероятность попадания случайной величины T в интервал ;

; ; ;

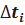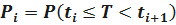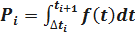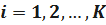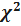– это случайная величина

Можно доказать, что если верна гипотеза H, то при распределение величины 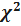независимо от вида функции f(t) стремится к распределению 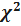с числом степеней свободы.

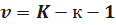; где K– число интервалов, r–число параметров функции f(t), оцениваемых по результатам опытов, по результатам статистической выборки объёма n.

Т.е. при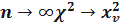

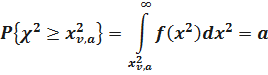
Пусть –такое число, что можно считать практически невозможным осуществление событий с такой вероятностью .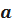

Если 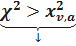то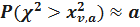

Т.е, в этом случае гипотеза Hотклоняется, т.е. выбранная теоретическая плотность вероятности не согласуется с результатом опытов.

S₀ – область принятия гипотезы H(выбранная теоретическая плотность вероятности согласуется с результатами опытов)

S₁ – область отклонения гипотезы H

n_i>5, n– порядок сотен.

Дата добавления: 2014-08-09; просмотров: 393; Нарушение авторских прав

Мы поможем в написании ваших работ!