Экспериментальная оценка надёжности изделий

Для решения теоретических и практических задач надёжности необходимо знать законы распределения исходных случайных величин. При оценке надёжности изделий может решаться задача определения по данным эксплуатации или специальных испытаний среднего времени безотказной работы 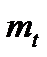, среднего времени восстановления .

Рассмотрим случайную величину Т - время безотказной работы. Приэксплуатации или испытаниях изделий в течении определённого временислучайная величина Т может принять п различных значений. Совокупностьэтих значений случайной величины Т называется статистической выборкойобъёма n. Эта выборка может использоваться для статистической оценкизакона распределения случайной величины Т.

Приведём пример статистической выборки для 10 однотипныхизделий.

При большом числе n удобнее перейти от статистической выборки кстатистическому ряду. Определяем диапазон значений случайной величиныТ.

,

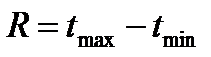где 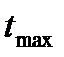, 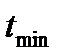- максимальное и минимальное значение случайной величины Т.

Этот диапазон R разбивается на интервалы длины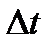

;

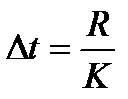где К- количество интервалов. Целесообразно выбирать число интервалов порядка 10 - 20. Обозначим через 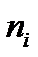количество значений случайной величины Т, попавших в интервал i - й длины . Полагаем ; i=1,2,…,K.

Определим частоту попадания в i - й интервал

.

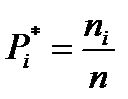Определяем статистическую плотность вероятности времени безотказной работы Т

.

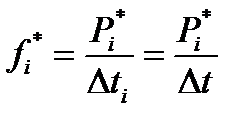Результаты сведём в таблицу:

Наглядное представление о законе распределения случайной величины Т дают статистические графики. Из них самые распространённые: полигон, гистограмма, статистическая функция распределения.

Полигон строится следующим образом: на оси абцисс откладываютсяинтервалы 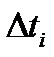, i= 1, 2,…,k , в серединах интервалов строятся ординаты,равные частотам 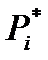и концы ординат соединяются.

Построение гистограммы: над каждым интервалом 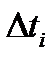, i= 1, 2,…,kстроится прямоугольник, площадь которого равна частоте 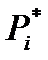в этом интервале.

Построение статистической функции распределения случайной величины Т. Над каждым интервалом проводится горизонтальная линия на уровне ординаты, равной величине накопленной частоты.

Второй способ построения статистической функции распределения случайной величины Т:

,

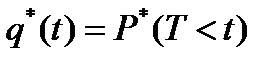где 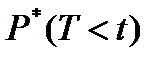- частота выполнения события Т<t.

,

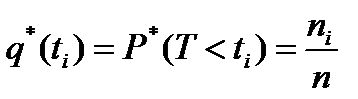где 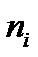- число опытов, при которых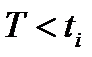

Статистическая плотность вероятности ^ и статистическая функцияраспределения 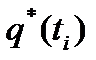случайной величины Т представляют статистический закон распределения случайной величины Т.

Дата добавления: 2014-08-09; просмотров: 420; Нарушение авторских прав

Мы поможем в написании ваших работ!