
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
Анализ надёжности систем при резервировании с дробной кратностью и постоянно включенным резервом
Определим количественные характеристики надёжности при постоянно включенном резерве. Резервированная система состоит из 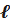 отдельных систем. Для её нормальной работы необходимо, чтобы исправными были не менее чем h систем. Кратность
отдельных систем. Для её нормальной работы необходимо, чтобы исправными были не менее чем h систем. Кратность 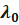 резервирования такой системы равна:
резервирования такой системы равна:
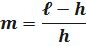
Допущения:
1) Отказы элементов удовлетворяют условиям простейшего потока случайных событий;
2) Переключающие устройства идеальны.
3) Основные и все резервные системы равнонадёжны.
Эти допущения означают, что для любой отдельно взятой системысправедлив экспоненциальный закон надёжности, причём все резервные
элементы находятся в рабочем состоянии с момента включениярезервированной системы в работу.
Резервированная указанным способом система будет работатьнормально при следующих возможных ситуациях:
- ни одна из систем не отказала
- отказала одна система
- отказали две системы
- отказали 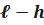 систем
систем
Принимая указанные ситуации за гипотезы, вероятность безотказной работы можно записать в виде 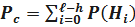 ;
;
где 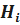 – гипотезе, заключающаяся в том, что резервированная система работает исправно при отказе i – любых систем;
– гипотезе, заключающаяся в том, что резервированная система работает исправно при отказе i – любых систем; 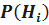 - вероятность появления гипотезы
- вероятность появления гипотезы 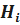 ;
; 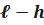 - число резервных систем.
- число резервных систем.
Отказы отдельных систем являются событиями независимыми, происходящими при одинаковых условиях работы отдельных систем. В этом случае к приведённым гипотезам применима частная теорема о повторении опытов, и вероятности гипотез подчинены биномиальному распределению:
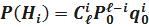 ;
; 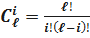 ,
,
где P0 – вероятность безотказной работы одной системы; q0–вероятность отказа одной системы.
Подставляя, получим
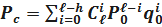 .
.
Так как
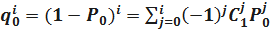 ,
,
то 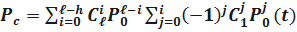
Или 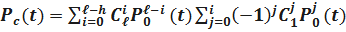 ,
,
где 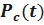 - вероятность безотказной работы резервированной системы.
- вероятность безотказной работы резервированной системы.
При принятых допущениях 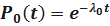 ,
,
где 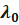 - интенсивность отказов любой одной из
- интенсивность отказов любой одной из 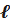 систем.
систем.
Определим среднее время безотказной работы системы.
Имеем:
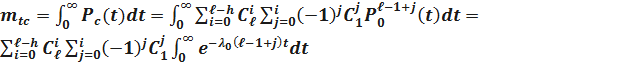 .
.
Введём обозначение
 .
.
Определим J. Имеем:
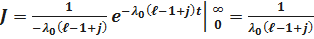 .
.
Тогда выражение для определения 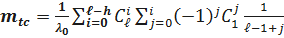 .
.
Или 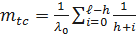
Получим выражение частоты отказов 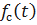 . Имеем
. Имеем
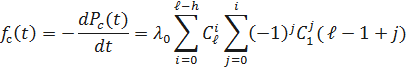
Получим выражение интенсивности отказов системы 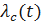 . Имеем
. Имеем
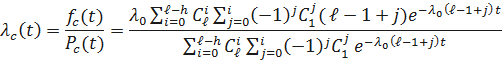
| <== предыдущая страница | | | следующая страница ==> |
| Основные количественные характеристики надёжности при поэлементном резервировании замещением | | | НАДЁЖНОСТЬ РЕМОНТИРУЕМЫХ (ВОССТАНАВЛИВАЕМЫХ) ИЗДЕЛИЙ |
Дата добавления: 2014-08-09; просмотров: 498; Нарушение авторских прав

Мы поможем в написании ваших работ!