Дисперсия портфеля

В общем случае дисперсия портфеля, состоящего из n инвестиционных активов, имеет вид:

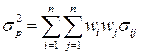(3.9)

В частном случае портфеля, состоящего из двух активов, дисперсия приобретает следующий вид:

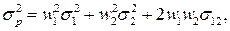или, с учетом формулы (3.8),

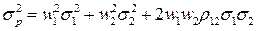(3.10)

В основе современного подхода к финансовому риску лежит предположение о невозможности правильно измерить риск отдельной ценной бумаги в отрыве от других составляющих инвестиционного портфеля[30]. Это положение легко проиллюстрировать, используя введенное понятие дисперсии портфеля как количественную меру риска.

Нашей целью будет показать на примере, как при прочих равных условиях можно добиться снижения риска инвестиционного портфеля, измеряемого его дисперсией, за счет комбинации инвестиционных активов, если корреляция последних не является строго позитивной. Предположим для простоты, что в распоряжении инвестора имеются лишь два инвестиционных актива – актив А и актив В. Для иллюстрации именно портфельного эффекта, предположим, следуя [Levy, Sarnat], что указанные выше активы имеют одинаковые распределения дохода, не имея при этом строго позитивной корреляции. Для определенности предположим, что корреляция между этими активами нулевая (ρ_АВ = 0). Предположим также, что инвестор может вложить имеющиеся у него средства либо только в актив А, либо только в В, либо 50% в А, 50% в В.

Если инвестор вкладывает все средства только в один актив, то он имеет равные шансы (то есть вероятность каждого исхода равна 0.5) как заработать 40 коп. на один вложенный рубль, так и потерять 20 коп. Это означает, что ожидаемый доход для портфеля, составленного из одного актива (А или В), составит 40•0.5 + (-20)•0.5 = 10 коп. на каждый вложенный рубль. Риск такого портфеля, измеряемый стандартным отклонением, составит [0.5(40 – 10)² + 0.5(-20 - 10)²]^0.5 = 30 коп. на каждый вложенный рубль. Соответственно, дисперсия такого портфеля составит 900 коп². Если инвестор решит распределить свои вложения поровну между активами А и В, то ожидаемый доход в соответствии с формулой (3.7) составит те же 10 коп.: Ř_p = w_A Ř_A + w_B Ř_B = 0.5•10 + 0.5•10 = 10 коп. При этом дисперсия портфеля, рассчитанная по формуле (3.10) с учетом нулевой корреляции (ρ_АВ = 0), составит:

σ_p² = w_А²σ_А² + w_В²σ_В² = 0.5²30² + 0.5²30² = 450 коп²,

а стандартное отклонение будет равно 21.2 коп. Таким образом, риск комбинированного портфеля существенно снизился по сравнению с портфелем, состоящим из одного актива. Этот эффект имеет место даже несмотря на то, что оба актива, использованных для комбинации, имеют идентичные показатели иска и дохода!

Полученный результат может быть достаточно просто проиллюстрирован и с позиций теории вероятностей.

Дата добавления: 2014-03-19; просмотров: 432; Нарушение авторских прав

Мы поможем в написании ваших работ!