
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
Лекция 6. Числовые характеристики дискретных случайных величин
Закон распределения полностью характеризует случайную величину, но если он неизвестен, а иногда и выгоднее пользоваться числами, которые описывают случайную величину суммарно– это числовые характеристики случайной величины (мат. ожидание, дисперсия и т.д.).
Определение. Математическим ожидание дискретной случайной величины называют сумму произведений всех возможных значений на их вероятности.
Математическое ожидание приближенно равно среднему значению случайной величины.
Замечание. Математическое ожидание числа появления событий в одном испытании равно вероятности этого события.
Можем доказать, что математическое ожидание приближенно равно и тем точнее, чем больше 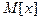 среднему арифметическому наблюдаемому значению случайной величины.
среднему арифметическому наблюдаемому значению случайной величины.
Замечание. Очевидно, что 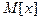 больше наименьшего и меньше наибольшего возможного значения. На числовой оси значения распоожены слева и справа от
больше наименьшего и меньше наибольшего возможного значения. На числовой оси значения распоожены слева и справа от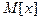 . В этом смысле
. В этом смысле 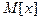 характеризует расположение распределения и поэтому его часто называют центром распределения.
характеризует расположение распределения и поэтому его часто называют центром распределения.
Свойства математического ожидания:
1. 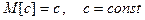 .
.
2. 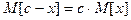
3. 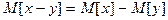
4. 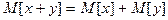
| <== предыдущая страница | | | следующая страница ==> |
| Биномиальное распределение дискретной случайной величины. Распределение Пуассона | | | Дисперсия дискретной случайной величины |
Дата добавления: 2014-02-26; просмотров: 637; Нарушение авторских прав

Мы поможем в написании ваших работ!