Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
АЭРОДИНАМИЧЕСКИЕ ХАРАКТЕРИСТИКИ ВИНТА
К аэродинамическим характеристикам винта относятся тяга Р, момент сопротивления М и мощность N, необходимые для вращения винта, и коэффициент полезного действия η в
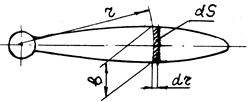
Как указывалось выше, лопасти винта, находящиеся во вращательном и поступательном движении, имеют разные скорости движения по отношению к набегающему потоку воздуха. Рассматривая два сечения лопасти (см. рис.4.9) на радиусах r и r+Δr и полученную между этими сечениями часть лопасти называется элементом лопасти на радиусе r. Площадь этого элемента лопасти будет dS=bdr.
| |||
| Рис.4.9. Геометрические размеры лопасти |
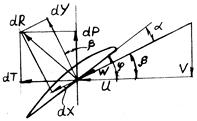
В обращенном движении, на указанный элемент лопасти набегает поток со скоростью V параллельной оси винта, и, во-вторых,- поток со скоростью U в направлении, перпендикулярном скорости V , дающие результирующую скорость W- скорость набегания потока на элемент лопасти. Угол между вектором W и хордой сечения есть угол атаки сечения α.
Угол φ между хордой сечения и вектором U (или, что тоже, плоскостью вращения винта) есть угол установки сечения лопасти, а угол β между векторами скоростей U и W - угол притекания. Такой элемент лопасти можно рассматривать как крыло и применить к нему общие формулы аэродинамики.
Подъемная сила для элемента лопасти:
dY=C y 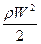 d S , (4.1)
d S , (4.1)
и лобового сопротивления
dX=Cx 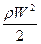 dS. (4.2)
dS. (4.2)
Как известно из аэродинамики, коэффициент лобового сопротивления Сx зависит от относительного размаха крыла. Какой же относительный размах принимать в данном случае? На первый взгляд, кажется, что следует принять бесконечный размах; но, как известно из аэродинамики, такое крыло не будет иметь индуктивного сопротивления. Поэтому оно не будет вызывать индуктивных скоростей, что противоречит тому, что должно быть в струе идеального пропеллера. Таким образом, если принять элемент лопасти за крыло бесконечного размаха, то следует каким-либо другим путем находить вызванную винтом скорость, и тогда треугольник скоростей в сечении лопасти следует принимать, как показано на рис. 4.5. Для того чтобы можно было воспользоваться этими формулами для определения тяги и мощности элемента лопасти, следует принять в них Сy и Сx для какого-то фиктивного относительного размаха, причем считать, что элемент работает в лопасти изолированно - без какого бы то ни было влияния соседних элементов. Далее следует допустить, что воздействие потока на такой элемент, несмотря на то, что он движется по винтовой траектории, подобно воздействию потока на крыло, движущегося поступательно. Это последнее предположение называется, обычно, гипотезой плоских сечений.
dY= Сy 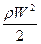 b dr (4.3)
b dr (4.3)
dX= Сx 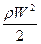 b dr (4.4)
b dr (4.4)
Абсолютные значения линейных размеров лопасти выразятся в относительной форме:
b= 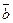 D, r=
D, r= 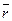
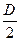 и dr=d
и dr=d 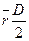
Выразим W через U и β.
U=ώr=2πns r= πns 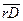 (4.5)
(4.5)
W2= 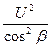 =
= 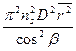 (4.6)
(4.6)
Значения элементарных подъемной силы dY и силы сопротивления dX с учетом (4.6) выразятся:
dY=Cy 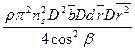 =Cy
=Cy 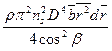 (4.7)
(4.7)
dX=Cx 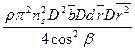 = Cx
= Cx 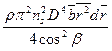 (4.8)
(4.8)
Рис. 4.10. Схема аэродинамических сил и скоростей, действующих на элемент лопасти |
Спроектируем подъемную силу и лобовое сопротивление элемента допасти на два взаимно перпендикулярных направления - на направление, параллельное оси винта, и на направление, совпадающее с плоскостью вращения винта (рис. 4.10).
Проекция dY на ось винта дает тягу dPэлемента лопасти:
dP=dYcosβ-dXsinβ= 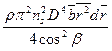
 (
( 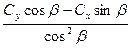 )(4.9)
)(4.9)
Проекция dX на плоскость вращения винта дает силу сопротивления вращению этого элемента:
dT=dYsinβ+dXcosβ= 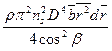 (
( 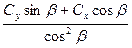 ) (4.10)
) (4.10)
Момент сопротивления вращению dM элемента лопасти:
dM=dT r=dT 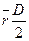 =
= 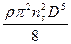 (
( 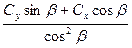 )
) 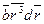 .(4.11)
.(4.11)
Потребная мощность вращения dN элемента лопасти:
dN=dM ω= dM 2πns= 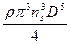 (
( 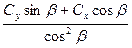 )
) 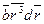 (4.12)
(4.12)
Общие тяга Р и мощность N для винта с i лопастями выразятся соответствующими интегральными зависимостями выражений (4.9) и (4.12):
P= 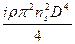
 (
( 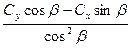 )
) 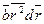 . (4.13)
. (4.13)
N= 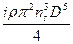
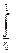 (
( 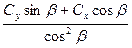 )
) 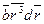 . (4.14)
. (4.14)
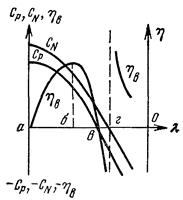
|
| Рис. 4.11. Аэродинамические характеристики винта при постоянном угле установки лопастей |
В формулах (4.13) и (4.14) подынтегральные выражения являются переменными функциями, зависящими от геометрических и аэродинамических характеристик лопасти винта, и, обозначив их соответственно СР – коэффициент тяги и С N – коэффициент мощности, получим окончательное выражение для тяги и мощности:
P= 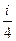 CP ρn2D4 , (4.15)
CP ρn2D4 , (4.15)
N= 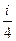 CN ρn3D5, (4.16)
CN ρn3D5, (4.16)
Коэффициент полезного действия винта ηв можно записать в виде:
ηв= 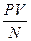 =
= 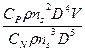 =
= 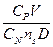 =
= 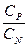 λ=
λ= 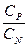 π
π 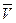 (4.17)
(4.17)
Относительная скорость 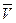 есть отношение скорости набегающего потока к окружной скорости на конце лопасти:
есть отношение скорости набегающего потока к окружной скорости на конце лопасти:
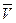 =
= 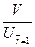 = tg
= tg 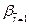
 =
=  =
= 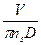
|
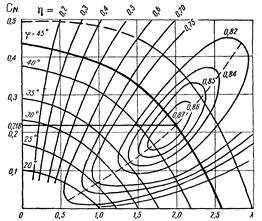
| Рис. 4.11а. Аэродинамическая характеристика винта |
Здесь отношение 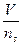 называется поступью винта (поступательное перемещение винта в податливой среде), а
называется поступью винта (поступательное перемещение винта в податливой среде), а 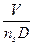 =λ- относительной поступью, тогда: λ=π
=λ- относительной поступью, тогда: λ=π 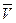 .
.
При подборе винта и при аэродинамическом расчете самолета задается мощность, передаваемая двигателем на винт, и требуется еще знание лишь коэффициента полезного действия винта,— тягой винта при аэродинамическом расчете обычно не пользуются. Удобно совместить кривые СN и ηтак, чтобы на кривых СN были нанесены соответствующие значения – η,тогда получается диаграмма, изображенная на рис. 4.11а.
На ней по оси абсцисс отложены λ, по оси ординат СN; кривые СN расположены по параметру угла установки винта φ; на кривых СN нанесены точки соответствующих КПД винта, при соединении которых образуются кривые одинаковых КПД. Как видно, кривые одинаковых КПД замкнутые и пересекаются соответствующими кривыми СN дважды. Ядро этих замкнутых кривых соответствует наибольшему значению КПД. Такая диаграмма называется аэродинамической характеристикой винта. На диаграмме должны быть обозначены условия испытаний, т. е, тип винтового прибора, диаметр испытанного винта, тип винта или его геометрическая характеристика, формы и размеры тела за винтом, скорость потока и число оборотов при испытании. Диаграмма, приведенная на рис. 197, является основной для подбора винтов.
| <== предыдущая страница | | | следующая страница ==> |
| КИНЕМАТИЧЕСКИЕ ХАРАКТЕРИСТИКИ ВИНА | | | РЕЖИМЫ РАБОТЫ |
Дата добавления: 2014-10-08; просмотров: 916; Нарушение авторских прав

Мы поможем в написании ваших работ!