
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
Определение дисперсии и ее свойства
Таким образом для оценки рассеяния вычисляют среднее значение квадрата отклонения, которое и называется дисперсией.
Определение. Дисперсией (рассеянием) дискретной случайной величины называется мат. ожидание квадрата отклонения случайной величины от ее мат. ожидания.
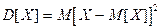
Пусть случайная величина задана законом распределеня:
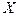
| 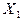
| 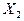 . . . . . .
| 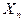
|
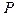
| 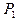
| 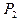 . . . . . .
| 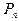
|
Тогда квадрат отклонения имеет следующий закон распределения:
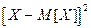
| 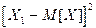
| . . . | 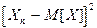
|
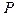
| 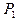
| . . . | 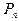
|
По определению дисперсии: 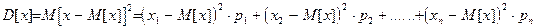
Теорема 6.2. Дисперсия равна разности между мат. ожиданием квадрата случайной величины Х и квадратом ее мат. ожидания: 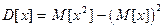 .
.
Доказательство: 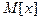 – постоянная величина
– постоянная величина 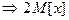 и
и 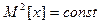 .
.
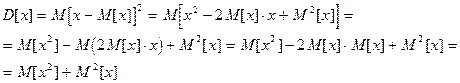
| <== предыдущая страница | | | следующая страница ==> |
| Дисперсия дискретной случайной величины | | | Свойства дисперсии |
Дата добавления: 2014-02-26; просмотров: 567; Нарушение авторских прав

Мы поможем в написании ваших работ!