
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
Действительные числа
Рациональных чисел недостаточно для решения ряда задач математики, так и в ее приложениях. Приведем некоторые из этих задач.
1) Во множестве рациональных чисел неразрешима задача измерения величин, даже отрезков. При выбранной единице измерения длины можно указать отрезки, длины которых не могут быть выражены рациональными числами. Еще древнегреческие математики обнаружили, что длину диагонали квадрата, сторона которого равна единице измерения, нельзя выразить рациональным числом. Рассмотрим аналогичную задачу.
Пусть дан прямоугольный треугольник с катетами 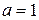 и
и 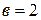 . Найти длину гипотенузы
. Найти длину гипотенузы 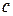 . Известно, что
. Известно, что 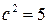 или
или 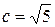 . Покажем, что
. Покажем, что 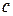 не может быть рациональным числом.
не может быть рациональным числом. 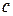 не является целым числом, т.к.
не является целым числом, т.к. 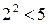 , а
, а 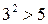 , между 2 и 3 нет натуральных чисел. Предположим, что
, между 2 и 3 нет натуральных чисел. Предположим, что 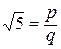 - рациональное число, причем можно считать, дробь несократима. По определению
- рациональное число, причем можно считать, дробь несократима. По определению 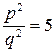 или
или 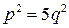 . Правая часть этого равенства делится на 5, т.е.
. Правая часть этого равенства делится на 5, т.е. 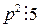 или
или 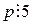 и
и 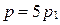 , где
, где 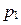 - натуральное число. Тогда
- натуральное число. Тогда 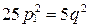 или
или 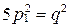 ,
, 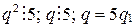 . Получили, что дробь
. Получили, что дробь 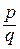 - сократима, что противоречит предположению.
- сократима, что противоречит предположению.
2) В поле 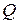 не разрешимы многие даже простейшие уравнения. Докажите, что уравнение
не разрешимы многие даже простейшие уравнения. Докажите, что уравнение 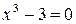 не имеет рациональных корней.
не имеет рациональных корней.
3) В рамках множества рациональных чисел не может быть обоснована теория пределов и другие фундаментальные теории математического анализа, связанные с ней, т.к. существуют сходящиеся последовательности рациональных чисел, пределы которых не являются рациональными числами. Например, рассмотрим представление 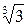 в виде бесконечной десятичной дроби,
в виде бесконечной десятичной дроби, 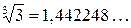 . Эта дробь не может быть периодической, согласно сказанному выше. Составим последовательность десятичных приближений по недостатку:
. Эта дробь не может быть периодической, согласно сказанному выше. Составим последовательность десятичных приближений по недостатку: 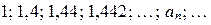 . Очевидно, что
. Очевидно, что 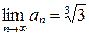 , т.е. эта последовательность рациональных чисел является сходящейся, но предел ее не содержится во множестве
, т.е. эта последовательность рациональных чисел является сходящейся, но предел ее не содержится во множестве 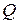 .
.
Эти и другие задачи приводят к заключению о необходимости расширения множества рациональных чисел. Таковым расширением является множество действительных (вещественных) чисел.
Начиная с XV и XVI вв. в связи с задачами нахождения корней алгебраических уравнений, математикам все чаще и чаще приходилось иметь дело с выражениями, полученными из исходных чисел не только с помощью арифметических операций, но и операции извлечения корней. А, по существу, это уже означало введение в математику, хотя и отчетливо неосознанное, иррациональных чисел. Природа иррациональных чисел отчетливо не была понятна еще и в XVIII в.
Только во второй половине XIX в. была четко осознана необходимость логического обоснования системы действительных чисел.
Логически обоснованное построение системы действительных чисел 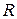 было осуществлено немецкими математиками Р. Дедекиндом (1831-1916), Г. Кантором (1845-1916), В. Вейерштрассом (1815-1897) и французским математиком Ш. Мере (1835-1911), при этом они опирались на разные исходные понятия. Построенные ими теории оказались эквивалентными.
было осуществлено немецкими математиками Р. Дедекиндом (1831-1916), Г. Кантором (1845-1916), В. Вейерштрассом (1815-1897) и французским математиком Ш. Мере (1835-1911), при этом они опирались на разные исходные понятия. Построенные ими теории оказались эквивалентными.
Более полно одно из построений системы 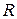 будет рассмотрено в курсе «Числовые системы».
будет рассмотрено в курсе «Числовые системы».
Мы рассмотрим вкратце упрощенный вариант построения системы действительных чисел, предложенный Вейерштрассом, придерживаясь в общих чертах изложения этого вопроса в школьном курсе математики.
О. Любую непериодическую бесконечную десятичную дробь называют представлением некоторого иррационального числа или просто иррациональным числом.
Отметим, что кроме иррациональных чисел вида  , где
, где 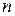 и
и  - натуральные числа, причем
- натуральные числа, причем 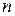 больше 1,
больше 1,  не является
не является 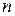 -ой степенью никакого другого натурального числа, существуют и другие бесконечные непериодические дроби.
-ой степенью никакого другого натурального числа, существуют и другие бесконечные непериодические дроби.
Рассмотрим, например, бесконечную десятичную дробь 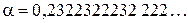 , покажем, что она непериодическая. Предположим, что эта дробь периодическая и длина периода равна
, покажем, что она непериодическая. Предположим, что эта дробь периодическая и длина периода равна 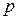 . Тогда период должен содержать хотя бы одну цифру три, поэтому в записи этого числа не может подряд стоять больше
. Тогда период должен содержать хотя бы одну цифру три, поэтому в записи этого числа не может подряд стоять больше 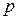 -1 двоек, а это противоречит тому, что, начиная с некоторого момента, найдутся участки, содержащие
-1 двоек, а это противоречит тому, что, начиная с некоторого момента, найдутся участки, содержащие 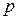 и более
и более 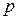 двоек. Следовательно,
двоек. Следовательно, 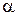 является иррациональным числом.
является иррациональным числом.
Подобного вида непериодических десятичных дробей можно построить бесконечное множество.
Упр. 28. Докажите, что бесконечная дробь 0,232233222333... непериодическая.
Присоединив к множеству рациональных чисел иррациональные числа, получим множество действительных чисел 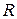 . Так как любое рациональное число можно отождествить с периодической десятичной дробью (без девятки в периоде), то можно дать единое определение действительному числу.
. Так как любое рациональное число можно отождествить с периодической десятичной дробью (без девятки в периоде), то можно дать единое определение действительному числу.
О. Действительное число – это есть бесконечная десятичная дробь.
| <== предыдущая страница | | | следующая страница ==> |
| Обращение периодических десятичных дробей в обыкновенные | | | Арифметические операции на множестве действительных чисел |
Дата добавления: 2014-03-11; просмотров: 564; Нарушение авторских прав

Мы поможем в написании ваших работ!