Обращение периодических десятичных дробей в обыкновенные

Нетрудно получить правила обращения периодических десятичных дробей в обыкновенные. Например, рассмотрим, дробь 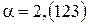. Это число можно представить в виде ,

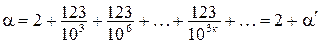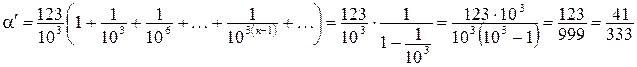, т.к. в скобках геометрическая прогрессия со знаменателем 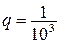. Следовательно, .

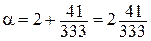Пусть 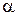- чистая периодическая десятичная дробь и 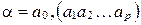, где 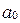- целая часть 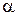. Число, стоящее в периоде обозначим через 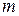, т.е. 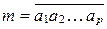, тогда 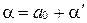, где 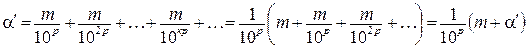или или 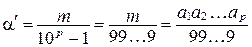, причем в знаменателе 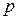девяток.

При обращении смешанной периодической десятичной дроби в обыкновенную пользуются следующим правилом: целую часть оставляют без изменения, в числителе дроби пишут разность всего числа, записанного после запятой, и предпериода, а в знаменателе – число, состоящее из стольких девяток, сколько цифр в периоде, со столькими нулями, сколько цифр в предпериоде.

Например, .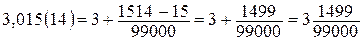

Упр. 27. Запишите в виде обыкновенных дробей числа .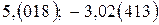

Любую конечную десятичную дробь, в том числе и целое число, можно записать в виде бесконечной десятичной дроби с нулем в периоде, например, .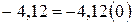

Таким образом, множество рациональных чисел можно отождествить с множеством бесконечных периодических дробей (без девятки в периоде).

Дата добавления: 2014-03-11; просмотров: 678; Нарушение авторских прав

Мы поможем в написании ваших работ!