Представление рациональных чисел в виде десятичных дробей

Известно, что десятичные дроби были предложены к употреблению нидерландским математиком и инженером Симоном Стевиным (Стивенсоном) (1548-1620) в 1584 году. Теория десятичных дробей была изложена в работах шотландского математика Джона Непера (1550-1617), который широко известен введением в математику логарифмов.

В XVI-XVII веках десятичные дроби постепенно входят в употребление. В России первые систематические сведения о десятичных дробях изложены в «Арифметике» Л. Магницкого, изданной в 1703 году.

В настоящее время в вычислениях с дробными числами мы чаще пользуемся их представлениями в виде десятичных дробей.

Различают конечные и бесконечные десятичные дроби. Среди бесконечных десятичных дробей выделяют периодические дроби.

О. Бесконечная десятичная дробь 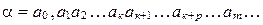называется периодической с предпериодом, содержащим 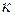цифр, и в периоде 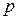цифр, если для любого 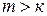цифра 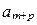совпадает с цифрой 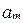, и записывается в виде .

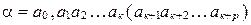Если предпериод не содержит ни одной цифры, то такую дробь называют чистой периодической десятичной дробью и записывают .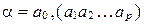

Теорема. Несократимая дробь 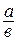тогда и только тогда представима в виде конечной десятичной дроби, когда каноническое разложение знаменателя имеет вид 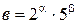, где 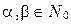, причем, по крайней мере, одно из них не равно нулю.

Д. Достаточность. Пусть имеет указанный вид и 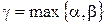. Тогда 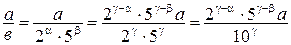, т.е. обыкновенная дробь представима в виде конечной десятичной дроби.

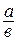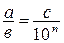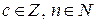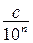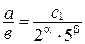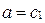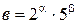Необходимость. Предположим, что дробь представима в виде конечной десятичной дроби, т.е. , где . Если сократима, то сокращение возможно лишь на некоторые степени 2 и 5, т.к. . После сокращения будем иметь , причем и , где .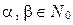

Предположим, что в каноническом разложении знаменателя несократимой дроби 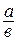имеется хотя бы один сомножитель, отличный от двойки и пятерки, тогда дробь 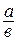будет представлена в виде бесконечной десятичной дроби. По известному алгоритму представления обыкновенных дробей в виде десятичной, заключающемуся в последовательном делении определенных чисел на число , число получающихся различных остатков не может быть больше -1. Но такой процесс деления потенциально бесконечный, следовательно, начиная с некоторого шага деления остатки начнут повторяться в определенном порядке, в том же порядке будут повторяться получающиеся при делении на цифры в частном, т.е. получим периодическую десятичную дробь.

Отметим, что при обращении обыкновенной дроби в десятичную этим способом не может получиться десятичная дробь с девяткой в периоде. В курсе «Теории чисел» будут строго обоснованы вопросы, относящиеся к представлению обыкновенных дробей десятичными.

Дата добавления: 2014-03-11; просмотров: 733; Нарушение авторских прав

Мы поможем в написании ваших работ!