
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
Числовые поля. Минимальность поля рациональных чисел
Следует отметить, что кроме поля рациональных чисел, существуют и другие числовые поля, например, как будет показано ниже, множество действительных чисел 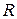 также является полем.
также является полем.
Теорема. Непустое числовое множество  тогда и только тогда является полем, когда выполняются следующие условия:
тогда и только тогда является полем, когда выполняются следующие условия:
1) для любых  и
и  из
из 
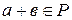 и
и 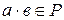 ;
;
2) для любого 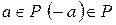 и для любого
и для любого 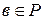 , где
, где 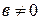 ,
, 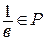 .
.
Д. Необходимость указанных условий непосредственно следует из определения поля.
Достаточность. Пусть для множества чисел  выполняются указанные два условия. Докажем, что
выполняются указанные два условия. Докажем, что  является полем.
является полем.
1) Коммутативный и ассоциативный законы сложения и умножения и дистрибутивный закон умножения относительно сложения выполняются на любом множестве чисел, то они выполняются и на множестве  .
.
2) Пусть 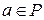 , тогда
, тогда 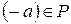 и
и 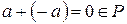 .
.
3) Пусть 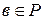 и
и 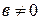 , тогда
, тогда 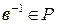 и
и 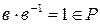 .
.
4) Очевидно, что 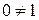 .
.
Таким образом,  является полем. Теорема доказана.
является полем. Теорема доказана.
Упр. 26. Докажите, что множество чисел 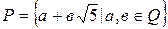 образует поле и
образует поле и 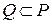 .
.
О. Поле 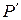 называют расширением поля
называют расширением поля  , если
, если 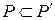 .
.
Теорема. Поле рациональных чисел 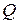 является минимальным числовым полем, т.е. содержится в любом числовом поле.
является минимальным числовым полем, т.е. содержится в любом числовом поле.
Д. Пусть  - произвольное числовое поле.
- произвольное числовое поле.
1) 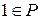 , если натуральное число
, если натуральное число 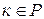 , то
, то 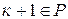 . По аксиоме индукции множество натуральных чисел
. По аксиоме индукции множество натуральных чисел 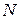 содержится в
содержится в  .
.
2) По предыдущей теореме  и если
и если 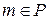 , то
, то  . Пусть
. Пусть 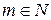 , тогда
, тогда  , т.е. множество целых чисел
, т.е. множество целых чисел 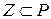 .
.
3) Рассмотрим произвольное рациональное число 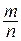 , где
, где 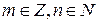 , т.е.
, т.е. 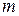 и
и 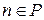 . Тогда согласно свойству полей
. Тогда согласно свойству полей 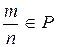 , т.е.
, т.е. 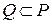 .
.
Теорема доказана.
Из этой теоремы следует, что все числовые поля содержат бесконечное число элементов. Приведенный в упр. 21 пример класса вычетов 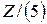 показывает, что существуют конечные поля.
показывает, что существуют конечные поля.
| <== предыдущая страница | | | следующая страница ==> |
| Поле рациональных чисел | | | Представление рациональных чисел в виде десятичных дробей |
Дата добавления: 2014-03-11; просмотров: 628; Нарушение авторских прав

Мы поможем в написании ваших работ!