
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
Делимость целых чисел и деление с остатком в кольце целых чисел
О. Пусть 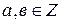 , говорят, что
, говорят, что  делится на
делится на  и пишут
и пишут  или
или 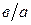 (
( делитель
делитель  ), если существует число
), если существует число 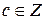 , удовлетворяющее условию
, удовлетворяющее условию 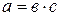 и
и 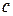 называют частным от деления
называют частным от деления  на
на  .
.
Ясно, что деление во множестве 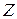 не всегда выполнимо.
не всегда выполнимо.
Исходя из определения умножения, можно доказать, что если существует частное от деления  на
на  , где
, где 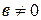 , то оно определяется однозначно, с другой стороны, не существует частного от деления числа, отличного от нуля, на нуль. Однако при таком определении
, то оно определяется однозначно, с другой стороны, не существует частного от деления числа, отличного от нуля, на нуль. Однако при таком определении 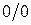 , т.е. нуль является делителем нуля, т.к., например,
, т.е. нуль является делителем нуля, т.к., например, 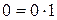 , но при этом нарушается однозначность деления.
, но при этом нарушается однозначность деления.
Для делимости целых чисел выполняются следующие свойства:
1) для любого 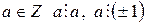 и
и 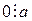 ;
;
2) если 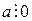 , то
, то  ;
;
3) если  и
и 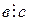 , то
, то 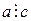 , т.е. отношение делимости транзитивно;
, т.е. отношение делимости транзитивно;
4) если 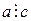 , то для любого
, то для любого  ;
;
5) если 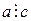 и
и 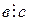 , то для любых целых чисел
, то для любых целых чисел 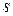 и
и 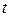
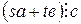 ;
;
6) если  , то для любого
, то для любого 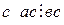 ;
;
7) если 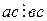 и
и 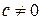 , то
, то  .
.
Докажите эти свойства самостоятельно.
О. Пусть  - целое число,
- целое число,  - натуральное число. Говорят, что произведено деление с остатком числа что
- натуральное число. Говорят, что произведено деление с остатком числа что  на
на  , если найдены целые числа
, если найдены целые числа 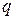 и
и 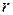 такие, что
такие, что 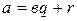 ,
, 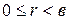 . При этом
. При этом 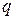 называется частным (неполным частным), а
называется частным (неполным частным), а 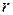 - остатком от деления
- остатком от деления  на
на  .
.
Теорема о делении с остатком. Для любых чисел  и
и  , где
, где 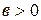 , существует единственная пара целых чисел
, существует единственная пара целых чисел 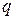 и
и 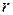 , удовлетворяющая условиям:
, удовлетворяющая условиям:
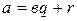 и
и 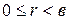 .
.
Д. 1) Докажем сначала возможность деления с остатком, когда 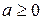 . Возможны два случая:
. Возможны два случая: 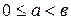 и
и 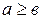 .
.
a) Пусть 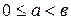 , тогда имеем
, тогда имеем 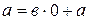 ; положим
; положим 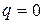 и
и 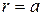 ;
; 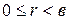 .
.
b) При 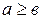 согласно свойству Архимеда найдется такое натуральное число
согласно свойству Архимеда найдется такое натуральное число 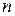 , что
, что  . Рассмотрим последовательность чисел
. Рассмотрим последовательность чисел
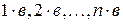 (1)
(1)
Ввиду дискретности множества натуральных чисел, в ряду (1) найдется наибольшее натуральное число 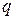 такое, что
такое, что 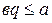 , но
, но 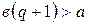 , т.е.
, т.е. 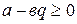 , но
, но 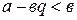 . Обозначим
. Обозначим 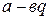 через
через 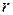 , т.е.
, т.е. 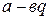 =
=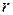 , тогда будем иметь
, тогда будем иметь 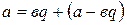 или
или 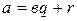 , где
, где 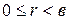 , т.е. при
, т.е. при 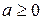 деление с остатком возможно.
деление с остатком возможно.
Пусть  , тогда
, тогда 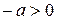 и согласно доказанному существуют целые числа
и согласно доказанному существуют целые числа 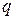 и
и 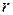 ,
, 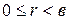 , что выполняется равенство
, что выполняется равенство 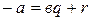 или
или 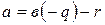 . Если
. Если 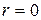 , то
, то  , если же
, если же 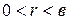 , то
, то 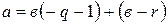 , где
, где 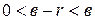 . Обозначив
. Обозначив 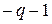 через
через 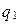 и
и 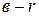 через
через 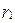 , будем иметь
, будем иметь 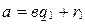 , т.е. и в этом случае деление с остатком возможно.
, т.е. и в этом случае деление с остатком возможно.
2) Докажем единственность деления с остатком. Пусть существуют два представления целого числа  :
:
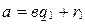 и
и 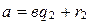 ,
, 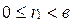 и
и 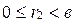 .
.
Предположим, что 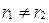 и
и 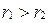 , тогда
, тогда  . Так как
. Так как 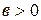 и
и 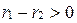 , то
, то 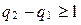 , но
, но 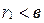 , следовательно,
, следовательно, 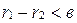 , с другой стороны,
, с другой стороны, 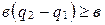 или
или 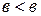 . Получили противоречие.
. Получили противоречие.
Упр. 19. Разделить с остатком -68045 на 78 и записать в виде деления с остатком.
Кольцо классов вычетов целых чисел по данному модулю 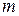
Ограничимся случаем, когда 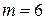 .
.
О. Пусть даны два целых числа  и
и  . Говорят, что они сравнимы по модулю 6 и пишут
. Говорят, что они сравнимы по модулю 6 и пишут 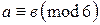 , если они при делении на 6 дают один и тот же остаток.
, если они при делении на 6 дают один и тот же остаток.
Нетрудно проверить, что если числа  и
и  при делении на 6 дают один и тот же остаток, то их разность делится на 6.
при делении на 6 дают один и тот же остаток, то их разность делится на 6.
Отношение сравнимости целых чисел является отношением эквивалентности, т.е. выполняются следующие свойства:
1) 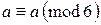 - рефлексивность;
- рефлексивность;
2) если 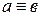 , то
, то 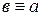 - симметричность;
- симметричность;
3) если 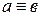 и
и 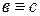 , то
, то 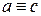 - транзитивность.
- транзитивность.
По теореме об эквивалентности множество целых чисел 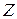 разобьется на непустые непересекающиеся классы, равноостаточные при делении на шесть чисел. Так как при делении на 6 остатками могут быть лишь числа 0, 1, 2, 3, 4, 5, то соответственно мы и получимшесть классов чисел, которые принято обозначать через
разобьется на непустые непересекающиеся классы, равноостаточные при делении на шесть чисел. Так как при делении на 6 остатками могут быть лишь числа 0, 1, 2, 3, 4, 5, то соответственно мы и получимшесть классов чисел, которые принято обозначать через 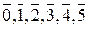 или
или 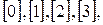
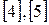 и называть классами вычетов по модулю шесть, а само множество этих классов – через
и называть классами вычетов по модулю шесть, а само множество этих классов – через 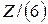 .
.
Упр. 20. Какому из классов вычетов принадлежат числа 142 и -142?
На множестве 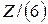 вводятся операции сложения и умножения следующим образом: под суммой классов
вводятся операции сложения и умножения следующим образом: под суммой классов 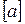 и
и 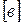 будем понимать класс
будем понимать класс 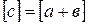 , а под их произведением – класс
, а под их произведением – класс 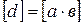 .
.
Проверьте, что таким образом определенные операции являются алгебраическими на множестве 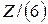 , т.е. сумма и произведение классов не зависят от выбора компонент в классах.
, т.е. сумма и произведение классов не зависят от выбора компонент в классах.
Нетрудно проверить, что при таком определении операций сложения и умножения для 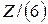 выполняются все свойства коммутативного кольца с единицей (проверьте самостоятельно).
выполняются все свойства коммутативного кольца с единицей (проверьте самостоятельно).
Таким образом, получили пример конечного числа.
Упр. 21. Заполните таблицу умножения классов.
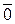
| 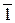
| 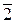
| 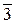
| 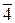
| 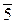
| |
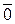
| ||||||
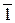
| ||||||
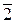
| ||||||
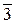
| ||||||
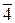
| ||||||
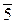
|
| <== предыдущая страница | | | следующая страница ==> |
| Отношение порядка на множестве целых чисел | | | Кольцо с делителями нуля |
Дата добавления: 2014-03-11; просмотров: 1010; Нарушение авторских прав

Мы поможем в написании ваших работ!