Биномиальное распределение. Распределения Пирсона и Стьюдента

Распределения Пирсона и Стьюдента

Оценка вероятности события

Центральная предельная теорема

Лекция 8. Некоторые законы распределения и их числовые характеристики

План лекции:

1. Биномиальное распределение
2. Распределение Пуассона
3. Нормальное распределение
4. Предельные теоремы

К этому распределению приводит схема Бернулли: пусть производится n независимых, однородных испытаний, в каждом из которых событие A может произойти с вероятностью p(A) = p, а ему противоположное - с вероятностью p(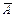) = 1 - p = q. Рассмотрим случайную величину z, которая принимает значение 1, если при испытании событие А произошло, и 0 – если не произошло (ее можно назвать индикатором события А).

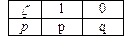
M(z) = 1×p + 0×q = p;

D(z) = (1–p)2×p + (0–p)2×q = pq.

Рассмотрим теперь дискретную случайную величину x, равную числу появлений события A при n испытаниях. Возможными значениями x являются все целые числа от 0 до n, а вероятность того, что x примет значение m, определяется ранее полученной формулой (1.16) Бернулли

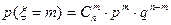. (2.18)

Для вычисления математического ожидания и дисперсии воспользуемся тем, что , где 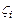независимы и имеют одинаковое распределение, заданное только что приведенной таблицей. Воспользуемся свойствами математического ожидания и дисперсии, учитывая независимость zk,

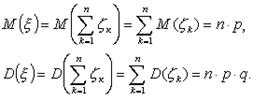(2.19)

Дата добавления: 2014-03-11; просмотров: 613; Нарушение авторских прав

Мы поможем в написании ваших работ!