Распределение Пуассона. Дискретная случайная величина называется распределённой по закону Пуассона, если её возможными значениями являются все неотрицательные целые числа (0

Дискретная случайная величина называется распределённой по закону Пуассона, если её возможными значениями являются все неотрицательные целые числа (0, 1, 2, ...), а вероятность того, что случайная величина x примет значение m, определяется формулой Пуассона

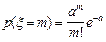. (2.20)

К этому закону, как уже отмечалось, мы приходим в схеме Бернулли при n ® ¥ и np = a (асимптотически). К нему же приводит задача о простейшем, стационарном (пуассоновском) потоке и ряд других.

Проверим выполнение условия нормировки

,

где мы воспользовались полученной в анализе формулой .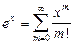

Аналогично, получим

.

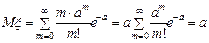Чуть более сложные выкладки дают Таким образом, математическое ожидание и дисперсия для этого распределения равны, то есть оно определяется одним параметром, что в ряде случаев является очень существенным.

Дата добавления: 2014-03-11; просмотров: 492; Нарушение авторских прав

Мы поможем в написании ваших работ!