
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
Арифметические операции на множестве действительных чисел
Выделяют две формы записи отрицательных дробных чисел, например, дробь 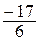 можно записать в виде
можно записать в виде 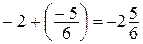 или
или 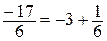 , т.е. во второй записи дробная часть является положительным числом.
, т.е. во второй записи дробная часть является положительным числом.
При записи бесконечной десятичной дроби 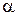 в виде
в виде 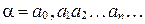 мы будем считать, что
мы будем считать, что 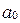 - произвольное целое число, а дробная часть – неотрицательное число. Чтобы особо выделить, что
- произвольное целое число, а дробная часть – неотрицательное число. Чтобы особо выделить, что 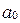 - отрицательное число, иногда над ним ставят знак «минус». Такую запись назовем стандартной записью действительного числа.
- отрицательное число, иногда над ним ставят знак «минус». Такую запись назовем стандартной записью действительного числа.
Для действительного числа 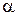 вводятся десятичные приближения по недостатку и по избытку с точностью до
вводятся десятичные приближения по недостатку и по избытку с точностью до 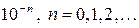 , обозначаемые соответственно
, обозначаемые соответственно 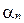 и
и 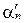 ;
;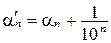 , для которых выполняется соотношение
, для которых выполняется соотношение 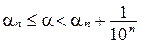 .
.
Если для конечных десятичных дробей сравнительно просто определяются операции сложения, умножение и сравнения, то при определении этих операций над бесконечными десятичными дробями возникают трудности принципиального характера. Поэтому при введении операций над действительными числами пользуются их десятичными приближениями.
О. Пусть даны два действительных числа 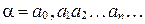 и
и 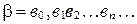 ,
, 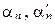 и
и 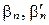 - соответствующие их десятичные приближения. Тогда под их суммой будем понимать действительное число
- соответствующие их десятичные приближения. Тогда под их суммой будем понимать действительное число 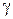 , удовлетворяющее неравенству
, удовлетворяющее неравенству 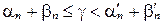 для любого
для любого 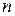 .
.
Можно доказать, что такое число 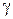 существует и определяется однозначно.
существует и определяется однозначно.
Определим произведение сначала двух положительных чисел 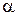 и
и 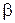 .
.
О. Число 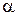 называется положительным, если найдется такое
называется положительным, если найдется такое 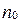 , что для всех
, что для всех 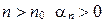 , и будем писать
, и будем писать 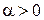 .
.
О. Число 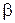 , противоположное положительному, называют отрицательным и пишут
, противоположное положительному, называют отрицательным и пишут 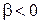 .
.
Множество всех положительных действительных чисел обозначим через 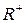 или
или 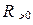 , отрицательных -
, отрицательных -  или
или 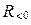 .
.
Модуль действительного числа определяется по аналогии с модулем целого числа.
О. Модулем действительного числа 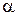 , обозначаемым через
, обозначаемым через 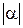 , называется число
, называется число
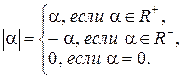
Как и для целых чисел можно приписать действительному числу 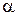 его знак
его знак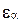 , нулю приписывают любой из знаков + или –. Тогда будем иметь соотношения
, нулю приписывают любой из знаков + или –. Тогда будем иметь соотношения 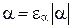 или
или 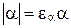 .
.
О. Под произведением двух положительных чисел 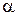 и
и 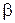 будем понимать действительное число
будем понимать действительное число 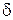 , удовлетворяющее неравенству
, удовлетворяющее неравенству 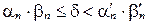 для любого
для любого 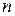 .
.
Можно доказать, что такое 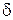 существует и определяется однозначно.
существует и определяется однозначно.
О. Если хотя бы одно из чисел 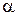 или
или 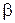 равно нулю, то будем считать, что
равно нулю, то будем считать, что 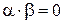 .
.
Заметим, что 0 можно представить в виде 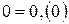 .
.
О. Пусть 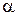 и
и 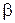 - произвольные действительные числа, тогда их произведение
- произвольные действительные числа, тогда их произведение
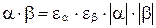 ,
,
где 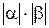 равно нулю или определено в
равно нулю или определено в 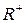 .
.
Можно проверить, что множество действительных чисел 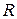 относительно определенных выше операций сложения и умножения является полем (выполнимость свойств поля для
относительно определенных выше операций сложения и умножения является полем (выполнимость свойств поля для 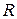 проверьте самостоятельно). Отметим, что число 1 относительно умножения, а 0 (нуль) относительно сложения и умножения во множестве
проверьте самостоятельно). Отметим, что число 1 относительно умножения, а 0 (нуль) относительно сложения и умножения во множестве 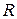 играют такую же роль, как во множествах
играют такую же роль, как во множествах 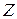 и
и 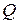 . Существование обратного элемента для
. Существование обратного элемента для 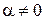 на данном этапе примем без доказательства.
на данном этапе примем без доказательства.
Примем без доказательства и существование корня натуральной степени 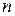 для любого неотрицательного действительного числа.
для любого неотрицательного действительного числа.
Отношение порядка на множестве действительных чисел 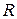
О.1. Пусть даны два действительных числа 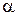 и
и 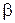 , записанные в стандартной форме,
, записанные в стандартной форме, 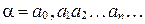 ,
, 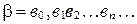 . Говорят, что
. Говорят, что 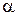 больше
больше 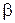 и пишут
и пишут 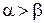 , если существует такое
, если существует такое 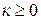 , что
, что 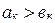 и
и 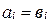 при всех
при всех 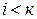 .
.
Существует и другое определение отношения порядка на 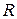 .
.
О.2. Говорят, что 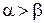 , если
, если 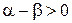 .
.
Упр. 29. Докажите эквивалентность этих двух определений.
Дизъюнкцию 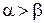 или
или 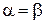 обозначают в виде
обозначают в виде 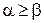 .
.
Можно ввести отношение симметричного отношения 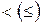 .
.
Упр. 30. Докажите, что отношение 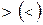 является отношением строгого линейного порядка на множестве
является отношением строгого линейного порядка на множестве 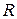 .
.
Множество действительных чисел 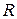 , как и множество рациональных чисел, является плотным множеством, т.е. для любых двух неравных действительных чисел
, как и множество рациональных чисел, является плотным множеством, т.е. для любых двух неравных действительных чисел 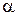 и
и 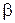 найдется действительное число
найдется действительное число 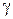 , заключенное между ними.
, заключенное между ними.
Проверьте, что если 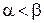 , то имеет место соотношение
, то имеет место соотношение 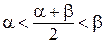 .
.
Множество действительных чисел может быть задано и с помощью системы аксиом. Отметим две из этих аксиом: аксиому Архимеда и аксиому полноты (непрерывности).
Аксиома Архимеда утверждает, что для любых действительных чисел 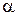 и
и 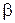 , где
, где 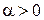 , найдется такое натуральное число
, найдется такое натуральное число 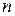 , что
, что 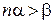 .
.
Пусть дано числовое поле  , в котором определено стандартное отношение порядка, т.е.
, в котором определено стандартное отношение порядка, т.е. 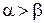 , если
, если 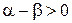 .
.
Аксиома полноты множества  имеет несколько формулировок. Мы ограничимся двумя формулировками полноты.
имеет несколько формулировок. Мы ограничимся двумя формулировками полноты.
О. Последовательность чисел 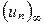 поля
поля  называется фундаментальной, если для любого
называется фундаментальной, если для любого 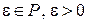 , найдется такое натуральное число
, найдется такое натуральное число 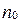 , что для любых
, что для любых 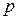 и
и 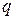 из
из 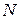 , где
, где 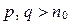 , выполняется неравенство
, выполняется неравенство 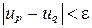 .
.
Отметим, что существует и другое, эквивалентное, определение фундаментальной последовательности.
Теорема. Всякая сходящаяся последовательность чисел поля  является фундаментальной.
является фундаментальной.
Д. Пусть 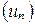 - сходящаяся последовательность чисел поля
- сходящаяся последовательность чисел поля  и
и 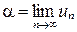 ,
, 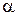 принадлежит самому полю
принадлежит самому полю  , либо содержится в некотором его расширении. Рассмотрим выражение
, либо содержится в некотором его расширении. Рассмотрим выражение 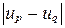 , где
, где 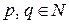 . Используя известные соотношения для модуля, будем иметь:
. Используя известные соотношения для модуля, будем иметь:
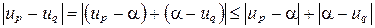 (1)
(1)
Пусть 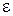 - произвольное положительное, по определению предела найдется такое натуральное число
- произвольное положительное, по определению предела найдется такое натуральное число 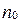 , что для всех
, что для всех 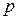 и
и 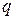 , больших
, больших 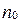 , будем иметь
, будем иметь 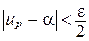 и
и 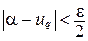 , тогда из (1) получим
, тогда из (1) получим 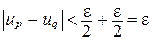 , т.е. последовательность
, т.е. последовательность 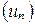 - фундаментальная. Теорема доказана.
- фундаментальная. Теорема доказана.
О. Числовое поле  называется полным (непрерывным), если любая фундаментальная последовательность чисел поля
называется полным (непрерывным), если любая фундаментальная последовательность чисел поля  сходится в этом поле.
сходится в этом поле.
О. последовательности стягивающихся вложенных отрезков. Последовательность отрезков 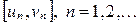 , чисел поля
, чисел поля  называется последовательностью стягивающихся вложенных отрезков, если выполняются следующие условия:
называется последовательностью стягивающихся вложенных отрезков, если выполняются следующие условия:
1) последовательность 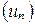 неубывающая, т.е.
неубывающая, т.е. 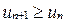 , а последовательность
, а последовательность 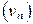 убывающая, т.е.
убывающая, т.е. 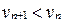 , для любого
, для любого 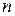 ;
;
2) для любого 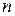
 ;
;
3) при 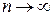 длина отрезка
длина отрезка 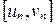 стремится к нулю.
стремится к нулю.
О. Числовое поле  называется полным (непрерывным), если для любой последовательности стягивающихся вложенных отрезков
называется полным (непрерывным), если для любой последовательности стягивающихся вложенных отрезков 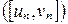 чисел этого поля существует единственное число из поля
чисел этого поля существует единственное число из поля  , принадлежащее всем отрезкам этой последовательности.
, принадлежащее всем отрезкам этой последовательности.
Можно доказать, что эти два определения полноты эквивалентны.
Было доказано, что множество рациональных чисел является плотным, но оно не является полным. Действительно, рассмотрим последовательность 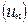 десятичных приближений числа
десятичных приближений числа 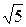 :
: 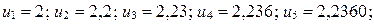
 . Нетрудно доказать, что
. Нетрудно доказать, что 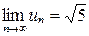 , т.к. для любого
, т.к. для любого 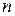
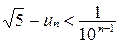 , т.е. эта последовательность, состоящая из рациональных чисел, является сходящейся, стало быть, является фундаментальной. Но предел этой последовательности не является рациональным числом.
, т.е. эта последовательность, состоящая из рациональных чисел, является сходящейся, стало быть, является фундаментальной. Но предел этой последовательности не является рациональным числом.
Для поля же действительных чисел справедливы утверждения:
1) любая фундаментальная последовательность действительных чисел сходится в поле действительных чисел;
2) для поля действительных чисел верен принцип вложенных отрезков.
Следовательно, поле действительных чисел 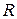 является полным (непрерывным).
является полным (непрерывным).
Упр. 31. Докажите, что число 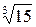 не может быть рациональным.
не может быть рациональным.
Упр. 32. Докажите, что бесконечная десятичная дробь 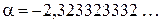 не является периодической.
не является периодической.
Замечание. Программные вопросы, относящиеся к множеству комплексных чисел, довольно полно и в доступной для студентов форме изложены в имеющихся вузовских учебниках, то мы предлагаем обратиться студентам к списку приведенной литературы.
| <== предыдущая страница | | | следующая страница ==> |
| Действительные числа | | | Абсолютные преимущества |
Дата добавления: 2014-03-11; просмотров: 713; Нарушение авторских прав

Мы поможем в написании ваших работ!