
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
Закон больших чисел
Лекция 7. Закон больших чисел. Теорема Чебышева. Функция и плотность распределения непрерывной случайной величины.
Для практики очень велико значение условий при выполнении которых совокупность многих случаев величина приводит к результату почти независимо от случая т.к. позволяет предвидеть ход явлений. Следует утверждение позволяет выяснить также условия эти утверждения и теоремы составляют содержание группы законов объединенных общим названием - закон больших чисел. К ним относятся: теорема Чебышева, теорема Бернулли и другие.
Теорема Чебышева является наиболее общим законом больших чисел, теорема Бернулли - к простейшим. Для их доказательства применимо неравенство Чебышева:
вероятность того, что отклонение случайной величины Х от её математического ожидания по абсолютной величине не меньше чем 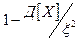 т.е.
т.е.
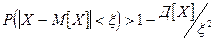 ;
;
Замечание: неравенство Чебышева имеет для практики ограниченное значение, т. к. Если предположить , что дисперсия не превосходит 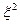 , то
, то
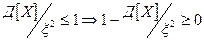
Таким образом неравенство Чебышева устанавливает тот факт, что
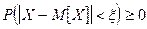
Теоретическое значение неравенства Чебышева весьма велико, им пользуются для доказательства теоремы Чебышева.
Теорема Чебышева: если 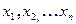 попарно независимые случайные величины, при
попарно независимые случайные величины, при
чём дисперсии их равномерно ограничены ( не превышают постоянного числа С ), то каким бы ни было положительное число 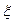 вероятность неравенства
вероятность неравенства
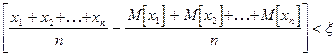
будет как угодно близка к 1, если число случаев велико.
Другими словами: в условиях теоремы
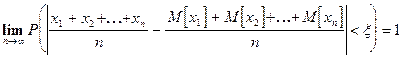
Сущность сформулированной теоремы такова:
хотя отдельные случайные величины могут иметь значительный разброс их среднее арифметическое рассеяны мало.
Таким образом нельзя уверенно предсказать, какие возможные значения примет каждая случайная величина, но можно предвидеть какие значения примет их среднее арифметическое. Итак6 среднее арифметическое большого числа независимой случайной величины ( дисперсии которых равномерно ограничены ) утрачивает характер случайной величины.
Значение теоремы Чебышева для практики: на теореме Чебышева основан широко применяемый в статистике выборочный метод, суть которого состоит в том, что по сравнительно небольшой случайной выборке судят о всей совокупности ( генеральной совокупности исследуемых объектов ).
Пусть производится n независимых испытаний в каждом из которых вероятность появления события 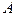 равна Р, можно ли предвидеть какова примерно будет относительная частота появления события.
равна Р, можно ли предвидеть какова примерно будет относительная частота появления события.
Положительный ответ на этот вопрос даст теорема доказанная Бернулли ( 1713 г.), более простое доказательство дал Чебышев в 1846 г.
Теорема Бернулли: если в каждом из n независимых испытаний вероятность появления события А постоянна, то для любого сколь угодно малого 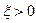
| <== предыдущая страница | | | следующая страница ==> |
| Среднеквадратичное отклонение | | | Функция и плотность распределения вероятности непрерывной случайной величины |
Дата добавления: 2014-02-26; просмотров: 837; Нарушение авторских прав

Мы поможем в написании ваших работ!