
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
Поле рациональных чисел
В кольце целых чисел неразрешимо даже такое простейшее уравнение, как 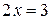 .
.
Задачи измерения пространственных, временных, физических и других величин приводят к необходимости учитывать совокупности частей единиц измерения. На примере даже измерения длины отрезка можно убедиться, что целые числа не могут обеспечить решение указанных выше задач измерения величин. Возникает необходимость введения новых чисел, которые могли бы характеризовать совокупности частей единицы, т.е. расширения целых чисел так, чтобы в этом расширении было возможно деление любых чисел (кроме деления на нуль). Таковым расширением является множество рациональных чисел, получающееся из множества целых чисел добавлением к ним дробных чисел. Использование дробей в вычислениях имеет глубокую историю.
О. Под дробью понимают любое отношение вида 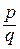 , где
, где 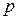 и
и 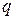 - целые числа,
- целые числа, 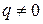 . Две дроби
. Две дроби 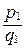 и
и 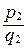 считаются равными, т.е.
считаются равными, т.е. 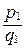 =
=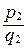 , тогда и только тогда, когда
, тогда и только тогда, когда 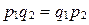 .
.
Обычно при записи дробей знаменатель считается натуральным числом, а числитель произвольным целым числом.
Среди дробей выделяют так называемые дробные числа, т.е. дроби, когда числитель не делится на знаменатель, например, 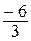 - дробь, но не дробное число, а
- дробь, но не дробное число, а  - дробное число.
- дробное число.
Таким образом, совокупность всех рациональных чисел 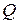 состоит из целых и дробных чисел.
состоит из целых и дробных чисел.
На множестве рациональных чисел 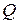 определяются операции сложения и умножения следующим образом.
определяются операции сложения и умножения следующим образом.
О. Пусть 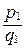 ,
, 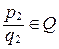 , тогда
, тогда 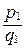 +
+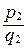 =
=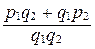 ,
, 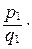
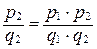 .
.
Непосредственно проверяется, что относительно указанных операций множество 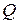 является полем.
является полем.
Упр. 24. Проверьте, что на множестве 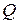 выполняются для указанных операций все свойства из определения поля.
выполняются для указанных операций все свойства из определения поля.
Отношение порядка на множестве 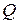
Будем считать, что в записи дробей знаменатели положительны.
О. Пусть даны два рациональных числа 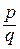 и
и 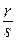 . Будем считать, что
. Будем считать, что 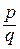 <
<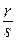 тогда и только тогда, когда
тогда и только тогда, когда 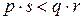 .
.
Отметим, что замечание о форме записи рациональных чисел, т.е. дробей, является существенным. Например, 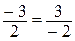 ,
, 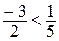 , т.к.
, т.к. 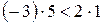 , с другой стороны, если взять дроби
, с другой стороны, если взять дроби 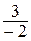 и
и  , то
, то 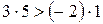 , т.е. число
, т.е. число 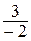 должно быть больше числа
должно быть больше числа  , чего быть не может.
, чего быть не может.
Теорема. Бинарное отношение “<” на множестве 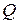 рациональных чисел обладает следующими свойствами:
рациональных чисел обладает следующими свойствами:
1) для любых 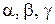 из
из 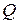 , если
, если 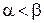 и
и 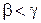 , то
, то 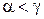 (транзитивность);
(транзитивность);
2) для любых 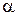 и
и 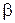 из
из 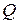 имеет место одно и только одно из трех соотношений:
имеет место одно и только одно из трех соотношений: 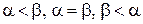 (связность);
(связность);
3) для любых 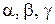 из
из 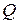 , если
, если 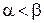 , то
, то 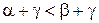 ;
;
4) для любых 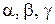 из
из 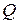 , если
, если 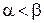 и
и 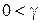 , то
, то 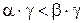 .
.
Соотношения 3) и 4) называют соотношениями стабильности.
Докажите эту теорему самостоятельно.
Относительно порядка на множестве 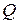 обладает свойством плотности, т.е. справедливо следующее утверждение: для любых
обладает свойством плотности, т.е. справедливо следующее утверждение: для любых 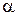 и
и 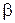 , где
, где 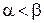 , найдется такое рациональное число
, найдется такое рациональное число 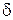 , что
, что 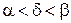 .
.
Докажите, что в качестве 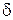 можно взять число
можно взять число 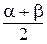 .
.
Упр. 25. Докажите, что если две несократимые дроби 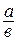 и
и 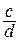 равны, то
равны, то 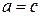 и
и 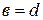 .
.
| <== предыдущая страница | | | следующая страница ==> |
| Упорядоченное поле | | | Числовые поля. Минимальность поля рациональных чисел |
Дата добавления: 2014-03-11; просмотров: 414; Нарушение авторских прав

Мы поможем в написании ваших работ!