Криптосистемы с открытыми ключами. Тестирование чисел на простоту и выбор параметров RSA

Изучаемые вопросы

1. Односторонние функции с секретом и ассиметричные системы

2. Криптосистема RSА

3. Криптосистема Эль-Гамаля

4. Криптосистемы на основе эллиптических кривых

5. Тест на основе малой теоремы Ферма

6. Тест Соловея-Штрассена и Эйлеровы псевдопростые числа

7. Тест Рабина-Миллера и сильные псевдопростые числа

8. Общие требования к выбору параметров RSA

9. Метод Гордона построения сильных простых чисел

10. Пример построения сильного простого числа

1. Односторонние функции с секретом и ассиметричные системы

Самым слабым звеном при реализации симметричных криптосистем в системах защищенного электронного документооборота, электронных банковских платежей и, особенно, электронной торговли является вопрос распределения ключей.

Для обеспечения обмена конфиденциальной информацией между двумя абонентами телекоммуникационной сети, должен быть сгенерирован ключ (возможно, одним из абонентов), а затем по некоторому защищенному каналу передан другим пользователям (другому абоненту). В качестве средства создания защищенного канала вновь может быть использована некоторая криптосистема.

Наибольшую остроту вопрос распределения и доставки ключей приобретает в случае невозможности заранее описать состав информационно-телекоммуникационной сети.

Для решения этой проблемы на основе результатов, полученных классической и современной алгеброй, были предложены системы с открытым ключом (СОК). В СОК для зашифрования не используются секретные ключи – они необходимы только при расшифровании (рис. 1).

Рис. 1. Криптосистема с открытым ключом

Главным понятием СОК является однонаправленная функция с секретом (one-way trapdoor function). Однонаправленную функцию с секретом f_t(x): D→R (2) легко вычислить для всех , но очень трудно обратить почти для всех значений из R. Однако, если используется некоторая секретная информация t, то для всех значений 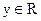легко вычислить величину , удовлетворяющую условию 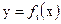(3).

Криптосистемы с открытым ключом, использующие однонаправленные функции с секретом, еще называются асимметричными (asymmetric cryptosystems).

В 1975 году в работе Диффи и Хеллмана, посвященной криптографии с открытым ключом, предложили несколько вариантов построения однонаправленных функций с секретом. Однако эти функции не были строго асимметричными, поэтому вскоре Диффи и Хеллман предложили более удачный вариант: показательную функцию по простому модулю.

Эта функция была использована в широко распространенном криптографическом протоколе – протоколе обмена ключами Диффи-Хеллмана (Diffie-Hellman key exchange protocol).

Ранее, в 1974 году, Меркл (Merkle) изобрел механизм согласования криптографического ключа путем явных асимметричных вычислений, получивших название головоломка Меркла.

Асимметричность головоломки Меркла заключается в том, что ее вычислительная сложность для законных участников протокола согласования ключа и для перехватчиков совершенно разная: легальные участники легко выполняют вычисления, а нелегальные — нет. Головоломка Меркла представляет собой первую эффективную реализацию однонаправленной функции с секретом.

Несмотря на то, что головоломка Меркла не подходит для применения в современных криптографических приложениях, ее влияние на криптосистемы с открытым ключом невозможно переоценить.

В последнее время стало известно, что первую криптосистему с открытым ключом разработал британский математик Кокс (Cocks) еще в 1973 году. Алгоритм Кокса, получивший название алгоритма с несекретным ключом шифрования, использовал сложность разложения целого числа на простые множители и, по существу, совпадал с криптосистемой RSA.

Первоначально алгоритм Кокса был засекречен и только в декабре 1997 года Группа по электронной защите средств связи (Communications Services Electronic Security Group – CESG) его рассекретила.

Несмотря на то, что вначале криптосистемы с открытым ключом были достоянием узкого круга лиц, именно благодаря открытым исследованиям они нашли два важнейших применения для создания алгоритмов цифровой подписи и механизмов обмена секретными ключами через открытые каналы связи.

В настоящее время алгоритмы шифрования с открытым ключом получили широкое распространение в информационных системах.

Так, алгоритм RSA фактически стал стандартом для открытых систем и рекомендован международной организацией по стандартизации ISO, соответствующие приложения лежат в основе электронной коммерции, осуществляемой через Internet.

Суть их состоит в том, что каждым абонентом сети генерируются два ключа, связанные между собой по определенному математическому закону.

Один ключ объявляется открытым, а другой закрытым (секретным).

Открытый ключ публикуется и доступен любому, кто желает послать сообщение владельцу секретного ключа. Секретный ключ сохраняется в тайне.

Исходный текст шифруется открытым ключом получателя и передается ему. Зашифрованный текст в принципе не может быть расшифрован тем же открытым ключом. Расшифровать сообщение возможно только с использованием секретного ключа, который известен только самому адресату.

Таким образом, односторонняя функция с секретом, используемая в асимметричной системе, является взаимнооднозначной, но вместе с тем обладает свойствами необратимости.

Необратимость понимается как практическая невозможность вычислить обратную функцию, используя современные вычислительные средства за обозримый интервал времени.

Поэтому, чтобы гарантировать надежную защиту информации, к СОК предъявляются два важных и очевидных требования.

1. Преобразование исходного текста должно быть вычислительно нереализуемым (необратимым) и исключать его восстановление на основе открытого ключа.

2. Определение закрытого ключа на основе открытого также должно быть невозможным на современном технологическом уровне. При этом желательна точная нижняя оценка сложности (количества операций) раскрытия шифра.

В основе современных криптосистем с открытым ключом вычислительно необратимые преобразования чаще всего строятся на основе следующих алгоритмических решений:

– разложение больших чисел на простые множители;

– вычисление логарифма в конечном поле;

– нахождение кратности точки (дискретный логарифм) на эллиптической кривой;

– вычисление корней алгебраических уравнений над кольцами и полями.

Отметим области применения СОК:

1. Средства шифрования передаваемых и хранимых данных.

2. Средства аутентификации пользователей и проверки целостности данных.

3. Механизмы распределения ключей.

Алгоритмы СОК работают медленнее, чем алгоритмы симметричных шифрсистем. Поэтому на практике предпочтительным является комбинированное использование СОК и симметричных систем. При этом СОК используется для создания механизмов распределения ключей, объем которых незначителен, а с помощью симметричных алгоритмов осуществляется шифрование больших информационных потоков.

Наибольшее распространение получили системы с открытым ключом на основе алгоритма RSA, криптосистема Эль-Гамаля и криптосистемы на основе эллиптических кривых.

2. Криптосистема RSА

Криптосистема RSA, разработанная в 1977 году, получила свое название в честь ее создателей: Рона Ривеста, Ади Шамира и Леонарда Эйдельмана.

Разработчики воспользовались тем фактом, что нахождение больших простых чисел в вычислительном отношении осуществляется достаточно просто, но не известен алгоритм, выполняющий за полиномиальное время разложение на простые множители больших чисел.

Доказано (теорема Рабина), что раскрытие шифра RSA эквивалентно нахождению такого разложения. Поэтому для любой длины ключа можно дать (современную практическую) нижнюю оценку числа операций для раскрытия шифра, а с учетом производительности современных компьютеров оценить и необходимое на это время.

Возможность реально оценить защищенность алгоритма RSA стала одной из причин популярности этой СОК на фоне десятков других схем. Поэтому алгоритм RSA используется в банковских компьютерных сетях, особенно для работы с удаленными клиентами (обслуживание кредитных карточек).

В настоящее время алгоритм RSA используется во многих стандартах, среди которых SSL, S-HТTP, S-MIME, S/WAN, STT и PCT. Кроме того, алгоритм RSA реализуется как в виде самостоятельных криптографических продуктов (PGP), так и в качестве встроенных средств в некоторых приложениях (Интернет-браузеры от Microsoft и Netscape).

Напомним ряд положений элементарной теории чисел, лежащих в основе этого алгоритма.

Наибольшим общим делителем двух целых чисел a и b называется наибольшее целое число, которое делит как a так и b. Обозначения: (a,b), или НОД(a,b). Числа a и b называются взаимно простыми, если (a,b) = 1.

Важным фактом является то, что НОД(a,b) можно выразить с помощью решений диофантового уравнения.

Пусть a > b и d = (a,b) (4). Тогда существуют целые числа x,y являющиеся решением уравнения xa + yb = d (4а).

Решение x,y,d уравнения xa + yb = d, при условиях a > b и d = (a,b), можно найти с помощью т.н. расширенного алгоритма Эвклида. Очевидно, достаточно решить уравнение, при положительных a и b.

Следовательно, для взаимно простых чисел m и b, m > b можно найти числа x,y, такие, что xm + yb = d = 1 (5). Приведем последнее равенство по модулю m, получим yb=1(modm) (5а).

Построенное число y называется числом, обратным к b по модулю m и обозначается через y = b^-1(modm) (5б). Такое число в диапазоне (1,...,m-1) является единственным.

Заметим, что по этой причине, множество H всех наименьших неотрицательных вычетов, взаимно простых с m, при умножении на любой свой элемент h, подвергается перестановке: h × H = H.

Рассмотрим степени числа a по модулю m, где a и m взаимно просты.

Пусть m = 11. Степени 1,2,…10, числа 2 таковы: 2,4,8,5,10,9,7,3,6,1.

Аналогично, степени числа 3 равны 3,9,5,4,1,3,9,5,4. В каждом случае имеется периодичность. Наименьшая длина периода для числа a по модулю m называется порядком (показателем, периодом) числа a по модулю m.

Порядок числа a по модулю m обозначается ord_ma (6).

Порядки чисел по модулю m различны. Существуют числа, являющиеся порядком одновременно для всех чисел, взаимно простых с m. Одно из них равно значению т.н. функции Эйлера φ(m), определяемой как количество чисел в последовательности 1,….,m, взаимно простых с m.

Из определения следует, что φ(p) = p - 1 для простого числа p и, кроме того, φ(1) = 1.

Функция Эйлера является мультипликативной: если (a,b) = 1, то φ(a,b) = φ(a)φ(b) (7).

Теорема Эйлера. Если (a,m) = 1, то a^φ(m) = 1modm (8).

Доказательство. При m = 2 теорема верна. Пусть m > 2 и a₁,...,a_k – все вычеты по модулю m, взаимно простые с модулем (по определению, k = φ(m)).

Пусть a > 1 – oдин из таких вычетов. Тогда множества {a_1,…,a_k} и {аа₁(modm),…aa_k(modm)} совпадают.

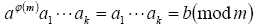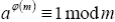Поэтому (9). Умножив обе части сравнения на (10), получим (10а).

Из теоремы Эйлера следует малая теорема Ферма: 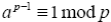(11), где p – простое, .

Случай a = 0(mod p) можно учесть в выражении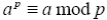

Существует общая формула для φ(m) при известном каноническом разложении m на степени простых чисел.

Пусть 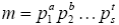(12), тогда (12а).

Таким образом, если n = pq , где p,q неравные простые числа, то (13).

Для модулей n указанного вида можно показать, что если e число, взаимно простое с φ(n), то отображение E_e,n:x → x^e(modn) является взаимно однозначным на множестве вычетов по модулю n. При этом, ed =1(modφ(n)), а обратным отображением является (14).

В криптосистеме RSA зашифрование блока сообщения m производится по формуле (рис. 15):

c = E_e,n(m),

Рис. 15 Формула зашифрования в криптосистеме RSA

Для расшифрования применяется обратная операция (рис. 16):

m = E_d,n(c)

Рис. 16 Формула расшифрования в криптосистеме RSA

Таким образом, открытым и секретным ключом криптосистемы являются соответственно (e,n) и d.

Построение ключа d при известных e,d,p,q легко осуществимо. При наличии соответствующих параметров функции E_e,n и E_d,n также легко вычисляются.

Если известны e и n, но p и q неизвестны, то E_e,n представляет собой одностороннюю функцию с секретом.

Построение E_d,n по заданным e и n равносильно разложению числа n на сомножители. В случае, когда p и q – достаточно большие простые числа, то разложение n практически невозможно. Это и является причиной стойкости криптосистемы RSA.

Рассмотрим принципы организации информационного обмена с использованием системы RSA. Вначале абонент i выбирает пару различных простых чисел p_i и q_i. Затем он вычисляет n_i = p_iq_i (17) выбирает случайный вычет e_i, взаимно простой с φ(n_i), и находит 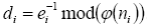(17а).

На общедоступном сервере (сайте) размещается справочная таблица, которая содержит открытые ключи абонентов (e_i,n_i).

Для передачи криптограммы от абонента i к абоненту j абонент i разбивает открытый текст на блоки и последовательно зашифровывает их с помощью преобразования 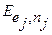(18), Абонент j производит расшифрование поблочно, применяя отображение 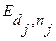(18а).

Очевидно, для того чтобы найти d_i, достаточно знание сомножителей p_i,q_i. Для современных технологических возможностей время выполнения наилучших из известных алгоритмов разложения для значений n ≈ 2¹⁰²⁴ слишком велико.

Рассмотрим учебный пример, иллюстрирующий применение алгоритма RSA. Зашифруем сообщение m = 3,1,2, состоящее из трех блоков.

1. Выберем простые числа: p = 3, q = 11.

2. Вычислим n = pq = 33 (19) и φ(n) = (p – 1)(q – 1) = 20 (19а).

3. Выберем случайное значение e = 7, (e,φ(n)) = 1 (20).

5. Вычислим секретный ключ d = 3 ed = 1(φ(n)) (21).

Открытый ключ – (7,33).

Зашифруем сообщение: m = 3,1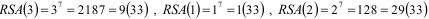,2.

(22).

Для расшифрования возведем каждый блок в степень d = 3 по модулю (23).

Секретный ключ для учебной системы легко найти перебором. На практике это невыполнимо, т.к. реальный размер модуля (длина битового представления) size(n) находится в диапазоне от 512 до 4096 битов.

Основные усилия в ходе практической реализации RSA приходятся на генерацию случайных больших простых чисел.

Есть очевидный путь решения задачи: случайно выбрать большое нечетное число n и проверить его делимость на множители в диапазоне .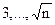

В случае неуспеха выбираем число n + 2 и так далее. Однако при больших n такой подход неосуществим.

Заметим, что из теории чисел известно, что вероятность того, что наудачу выбранное число порядка n будет простым, оценивается как 1/ln(n) (24).

В принципе в качестве p и q можно использовать «почти» простые числа, то есть такие числа, для которых вероятность того, что они простые, стремится к 1. Но в случае, если использовано составное число, а не простое, криптостойкость RSA падает. Имеются неплохие алгоритмы, которые позволяют генерировать «почти» простые числа с произвольно малой вероятностью ошибки.

Другая проблема – какой длины следует использовать ключи?

Полезно привести длины параметров RSA в битах, установленные и рекомендуемые французскими специалистам для практических приложений.

1. Сомножители RSA – модуля n = pq должны выбираться случайно и быть одинаковой длины.

2. Длина секретного ключа d должна быть сравнима с размером модуля n.

3. Длина открытого ключа e должна быть строго более 16 битов.

4. До 2010 года разрешается использовать значения модуля длиной не менее 1536 битов, однако рекомендуется – не менее 2048 битов.

5. С 2010 года по 2020 год разрешается использовать значения модуля длиной не менее 2048 битов.

6. После 2020 года предполагается использовать значения модуля длиной не менее 4096 битов.

Следующий немаловажный аспект реализации RSA – вычислительный.

Ведь приходится использовать аппарат арифметики больших чисел.

Следует учитывать, что, по сравнению с тем же алгоритмом DES, для RSA требуется в тысячи и десятки тысяч раз большее время.

3. Криптосистема Эль-Гамаля

В отличие от RSA асимметричная криптосистема Эль-Гамаля основана на проблеме дискретного логарифма.

Соответствующая односторонняя функция является показательной функцией по простому модулю p: секретные параметры входят в показатели степеней.

Возведение числа в степень в конечном поле выполняется легко, в то время как восстановление показателя степени по значению функции (то есть нахождение дискретного логарифма) при больших p является сложной вычислительной задачей.

Особенностью этой криптосистемы является то, что дискретный логарифм не является односторонней функцией с секретом. Поэтому для ее обращения отправитель сообщения формирует дополнительную информацию на основе разового ключа, которую получатель может использовать для чтения сообщения, защищенным от утечки информации способом.

В криптосистеме Эль-Гамаля для построения пары асимметричных ключей выбирается большое простое число p и два псевдослучайных числа, меньших p – 1.

Одно из них, g, должно быть элементом большого порядка по модулю p, скажем, первообразным корнем. Второе число, x, выбирается в качестве секретного ключа. Полагается, что сообщения – вычеты по модулю p.

Открытым ключом является тройка чисел p,g,y, = g^x(p) (25).

Для каждого сообщения формируются дополнительные данные, играющие роль лазейки для конкретного сеанса шифрования.

Для зашифрования сообщения m выбирается псевдослучайное число k (рандомизатор, разовый ключ) с условием НОД(k, p – 1) = 1. Рандомизаторы не должны повторяться и должны содержаться в секрете.

Затем вычисляются числа a = g^x(p) – лазейка и b = y^xm(p) – шифр текст (26).

Криптограммой является пара блоков данных a,b.

Для расшифрования достаточно получить сомножитель y^k, что можно сделать с помощью секретного ключа, вычислив значение a^x = g^kx(p) (27).

Действительно y^k = g^xk(p), поэтому m = a^-xb(p).

Таким образом, обеспечивается защищенный информационный обмен без предварительной рассылки секретных ключей.

4. Криптосистемы на основе эллиптических кривых

Для построения СОК могут быть использованы эллиптические кривые – математические объекты, определенные над конечными полями.

Для случаев характеристик поля p = 2, p = 3, p > 3, алгоритмы вычисления значений, связанных с реализацией подобных СОК, существенно различаются. Вместе с тем, основные принципы, на основе которых построены СОК на эллиптических кривых, в идейном смысле одинаковы.

Интересно отметить, что, в отличие от рассмотренных ранее криптосистем, построение открытых параметров для систем на эллиптических кривых является сложной алгоритмической проблемой. В данном случае эффект от стандартизации криптоалгоритмов особенно ощутим.

Для упрощения изложения, рассмотрим эллиптические кривые над простым полем характеристики p > 3.

Элиптическая кривая (ЭК) над полем вычетов по модулю p > 3 непосредственно связана с решениями сравнения y² = x³ + ax + b(modp) (28), при т.н. условии невырожденности кривой: 4a³ + 27b² ≠ 0.

Указанное сравнение называется уравнением кривой в афинных координатах.

Каждое решение x,y сравнения y² = x³ + ax + b(modp) называется точкой кривой P(x,y) (28а).

Множество решений сравнения y² = x³ + ax + b(modp) можно расширить таким образом, что расширенное множество станет коммутативной группой E. Эта группа называется группой точек на эллиптической кривой.

Групповой закон в группе E называется сложением. Основной причиной, позволяющей построить группу E, является возможность построения новых решений уравнения кривой, исходя из уже известных. Оказывается, если даны решения P₁(x₁,y₁) и P₂(x₂,y₂) то «практически всегда» можно найти третье решение, используя знание координат первых двух.

Операция, сопоставляющая двум (возможно, одинаковым) точкам их «сумму» P₁(x₁,y₁) + P₂(x₂,y₂) = P₃(x₃,y₃) (29), в аффинных координатах записывается в виде дробных выражений, поэтому при вычислениях может возникнуть особенность, если в соответствующем знаменателе появится нулевое значение (по модулю p ).

Очевидно, это единственная ситуация, когда возникает особенность.

Следовательно, ей можно сопоставить некоторое обозначение (O) и расширить множество решений уравнения кривой, добавив символ O, имитируя тем самым существование дополнительного элемента, называемого бесконечно удаленной точкой.

Можно показать, что если для операции «+» считать O нейтральным элементом, то расширенное множество точек кривой превращается в коммутативную группу, а сама операция – в групповой закон.

На самом деле, для аналитического описания расширенного множества точек кривой следует использовать т.н. проективные координаты, в которых точки кривой будут задаваться не парой, а тройкой чисел.

Оказывается, в этом случае все точки кривой будут равноправными и будут подчиняться более общему групповому закону.

Групповой закон в аффинных координатах был открыт при исследованиях эллиптических кривых на обычным полем вещественных чисел, что «подсказало» вид соответствующих преобразований над конечными полями.

Сложение двух точек ЭК над полем вещественных чисел можно сформулировать в виде геометрического построения, связывающего координаты точек-слагаемых с координатами точки-суммы (рис. 30).

Для этого следует учитывать, что если прямая пересекает ЭК в двух точках расширенной кривой, то она пересекает кривую в третьей точке (точка касания считается двойной точкой).

Рис. 30. График эллиптической кривой y² = x³ - 3x + 4 (а), сложение двух

точек (б), кратная точка (в).

Для сложении точек P и Q кривой (рис. 30б) проводим через P и Q прямую. Она пересечет ЭК в некоторой третьей точке 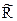Проведем через 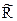прямую, параллельную оси ординат, которая пересечет ЭК в некоторой точке R, которую примем за сумму точек кривой: R = P + Q .

Если P = Q, то точка 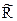является пересечением кривой и касательной к кривой в точке P. В соответствующих случаях полагаем, что прямые параллельные оси ординат проходят через бесконечно удаленную точку O.

Указанное геометрическое построение называется методом секущих и касательных.

Пусть P = (u,v). Обозначим . Очевидно, что при нашем построении R=(x,y), а R = (x, – y). Рассмотрим точку R + P. Пользуясь геометрическим построением, легко проследить, что R + Р, Q. Иными словами, прибавление к точке R = P + Q точки P эквивалентно «вычитанию» точки P из точки R. Таким образом, для определения операции вычитания, обратной сложению положим 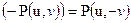(31).

Пусть G₁ = G, G₂ = G + G и т.д. Исходя из точки G, можно построить последовательность точек G₁,...,G_n-1,G_n = O некоторой длины n.

Если записывать подобное k -кратное сложение на кривой в виде kG, положив 0G =0 то, очевидно, коэффициент k можно приводить по модулю n и рассматривать выражения вида uP + vQ и u(vP) Операция kG называется скалярным умножением точки на k. Наименьшее целое n, для которого Gn = O, называется порядком точки G.

Используя аналитическую геометрию, можно показать, что групповой закон соответствует некоторым правилам, которые, в случае конечного поля характеристики p > 3, сводятся к следующему.

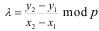
1. 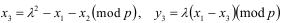(32), где ,

если и , если P₁ = P₂.

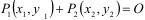2. Если знаменатель l обращается в нуль, то (32а)

3. Операция, обратная к сложению: 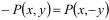(32б)

4. Для любой точки P расширенной кривой: . (32в)

Как правило, при построении СОК на эллиптической кривой используется точка G большого простого порядка n. Все операции в СОК осуществляются над точками вида kG, которые образуют циклическую подгруппу группы E.

Покажем, как можно построить аналог алгоритма Диффи-Хеллмана на эллиптической кривой. Исходными параметрами являются сама кривая E над конечным полем и точка G большого простого порядка n.

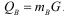Пользователи криптосистемы независимо генерируют секретные большие числа m_A и m_B, которые являются параметрами для формирования общего секретного ключа. На их основе вычисляются открытые ключи 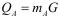и (33).

Произведя обмен открытыми ключами, каждый из абонентов может сформировать общий ключ (34).

Стойкость СОК основана на сложности задачи дискретного логарифмирования на кривой. Эта задача состоит в нахождении скалярного множителя k из соотношения
P = kG (35) и, в общем случае, является вычислительно недоступной.

Наиболее трудоемким этапом вычисления открытых параметров эллиптической кривой является определение простого числа n, которое является делителем количества #E элементов в группе E.

Как правило, вычисление n сводится к вычислению #E с его последующей факторизацией. Для вычисления #E используются сложные алгоритмы. Известны простые ограничения на коэффициенты уравнения ЭК, при которых либо , либо факторизация #E осуществима.

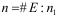Теоретически группа E состоит из не более, чем двух циклических подгрупп. Обычно параметры кривых таковы, что порядок n₂ одной из подгрупп очень мал и определяется сравнительно легко. После чего n вычисляется в виде (36).

Общие алгоритмы вычисления #E существуют, но являются сложными и трудоемкими.

Для числа #E имеются оценки. Например, неравенство Хассе: 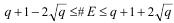, где q = p^r – количество элементов в поле характеристики p. Таким образом, 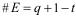где .

Для некоторых кривых число #E можно вычислить теоретически.

Кривые, для которых #E = p называются аномальными, а кривые для которых t = 0(p) – суперсингулярными.

Для кривых этих типов известны эффективные методы дискретного логарифмирования.

Тем не менее, существует класс криптопротоколов, в которых существенно используются свойства именно суперсингулярных эллиптических кривых.

Интересно отметить, что многие криптографические системы, разработанные на основе системы RSA, порождают аналоги на эллиптических кривых над кольцом вычетов Z/nZ для составного числа n = pq, где p,q ‑ различные простые числа.

Эллиптическая кривая E_n над Z/nZ задается теми же алгебраическими уравнениями, что и в случае простого модуля. Например, кривая задается как множество решений основного сравнения y² = x³ + ax + bmodn (37), при НОД(4a³ + 27b²,n) = 1 с бесконечно удаленной точкой O.

Операции на E_n выполняются по формулам, соответствующим методу секущих и касательных. К сожалению, такой объект не является группой.

Поэтому вместо E_n рассматривается т.н. прямая сумма кривых E_n = E_p+E_q: (38) другой объект, который «мало» отличается от E_n.

Каждый элемент E_n – четырехмерный вектор, состоящий из двух точек кривых E_p и E_q.

Если пара (x,y) удовлетворяет основному сравнению для E_n, то пары вычетов (xmodp, ymodp) и (xmodq, ymodq) автоматически удовлетворяют тому же сравнению по модулям p и q соответственно.

Напомним, что Китайской теоремой об остатках называется следующее утверждение.

Пусть числа m₁,m₂,…..,m_k попарно взаимно просты и M = m₁m₂,…,m_k.

Тогда единственное по модулю M решение системы сравнений x = c_imodm_i, i = 1,..,k, имеет вид: , где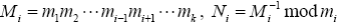

Действительно, в указанном выражении для x слагаемое c_iM_iN_i сравнимо с c_i по модулю m_i, а все прочие сравнимы по этому модулю с нулем.

В силу Китайской теоремы об остатках, x и y однозначно восстанавливаются по значениям (xmodp, xmodq) и (ymodp, ymodq).

Однако, вместе с бесконечно удаленной точкой O, группа E_n содержит совокупность точек вида Поэтому E_n состоит из точек кривой E_n и некоторого множества особых точек.

Приведем основные свойства E_n, близкие к свойствам E_n, что позволяет строить RSA-подобные криптосистемы.

1. Метод секущих и касательных, в случае, когда он определен для E_n, совпадает с групповой операцией в En.

Таким образом, если сложение конкретных точек в E_n выполнимо, то оно выполнимо без факторизации n.

2. При больших p и q, с вероятностью, близкой к единице, умножение точки на скаляр в En ведет себя как аналогичная операция в E_n.

Суть этого утверждения в следующем.

Положим N = НОК(#E_p, #E_q) (39). Тогда (kN + 1)P = P (39а) для подавляющего числа точек 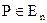и любых целых k.

Рассмотрим аналог системы RSA с использованием эллиптической кривой. Открытым ключом является пара N,e, где N = НОК(#E_p, #E_q), (N,e) = 1 (40), секретным – число d, такое, что ed = 1mod N (40а).

Шифртекст сообщения m, которое сопостовляется заранее выбранным способом некоторой точке M кривой E_n, отправитель получает с помощью скалярного умножения в виде C = eM (41). Получатель, зная число d, восстанавливает M = deM = dC (41а).

Оказывается, однако, что сопоставление 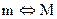может потребовать факторизацию n, т.е. указанная схема шифрования, вообще говоря, не является корректной. Тем не менее, существует ряд более совершенных RSA-подобных криптосистем, например, криптосистема Демитко (для кривых общего вида), либо криптосистема Кувакадо-Кояма для кривых вида y² = x³ + b(modn).

5. Тест на основе малой теоремы Ферма

При построении асимметричных криптосистем, возникает необходимость построения сверхбольших псевдослучайных простых чисел, обладающих теми или иными специфическими свойствами.

Во многих случаях, например, в случае RSA, большие простые числа являются ключевыми параметрами.

Соответствующие вычислительные процедуры включают в себя алгоритмы, реализующие этап проверки чисел на простоту. В литературе и криптографической практике подобные алгоритмы носят название тестов.

В основе тестов лежат т.н. критерии простоты. Существует два типа критериев простоты: детерминированные и вероятностные.

Детерминированные тесты позволяют доказать, что тестируемое число – простое. Практически применимые детерминированные тесты способны дать положительный ответ не для каждого простого числа, поскольку используют лишь достаточные условия простоты.

Детерминированные тесты более полезны, когда необходимо построить случайное большое простое число, а не проверить простоту, скажем, некоторого единственного числа.

Детерминированный тест используется, например, в процедурах вычисления несекретных параметров цифровой подписи типа Эль Гамаля, установленных ГОСТ 34.310. Этот тест основан на следующей теореме.

Теорема. (Демитко). Пусть n = qR + 1 (42), где q – простое, R– четное и R < 4(q + 1).

Если существует a такое, что a^n-1 = 1(modn) и a^(n-1)/q ≠ 1(modn) (42а), то число n – простое.

В отличие от детерминированных, вероятностные тесты можно эффективно использовать для тестирования отдельных чисел, однако их результаты, с некоторой вероятностью, могут быть неверными.

К счастью, ценой количества повторений теста с модифицированными исходными данными вероятность ошибки можно сделать как угодно малой.

При построении вероятностных критериев простоты возникает ряд типичных вопросов, которые удобно рассмотреть на примере, в качестве которого выберем тест на основе малой теоремы Ферма. Как известно, эта теорема утверждает, что если n – простое, то для всех a, взаимно простых с n, выполняется условие (сравнение Ферма): 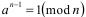(43)

Таким образом, если сравнение Ферма не выполнено, хотя бы для одного числа из множества 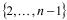, то a – составное.

Тест на основе малой теоремы Ферма заключается в следующем.

Псевдослучайно выбираем вычет 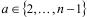и проверяем условие .

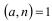Если это условие не выполнено, значит, n– составное. Проверяем сравнение Ферма.

Если оно не выполняется, то число n – составное. Иначе, повторяем тест для другого значения a.

Очевидно, основной вопрос состоит в том, чтобы оценить, в какой мере тест является эффективным. Прежде всего, следует выяснить, существуют ли составные числа n, для которых при некотором a выполняется условие малой теоремы Ферма. Оказывается это так, поскольку существуют контрпримеры:

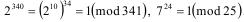(43а).

Назовем составное нечетное число n псевдопростым по основанию a, если пара чисел a,n удовлетворяет сравнению Ферма (43).

Оказывается, можно показать, что для любого a существует бесконечно много псевдопростых чисел по основанию a.

Основные свойства псевдопростых чисел таковы.

Теорема. Пусть n – нечетное составное число.

Тогда:

а) n - псевдопростое по основанию a в том и только том случае, когда (a,n) = 1 и (44)

б) если n – псевдопростое по основаниям a и b, то n – псевдопростое по основаниям ab и ab^-1(modn) (45);

в) множество 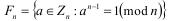(46) образует мультипликативную подгруппу в мультипликативной группе обратимых элементов кольца вычетов по модулю n;

г) если n не является псевдопростым по основанию a, хотя бы для одного числа a, то (47) (здесь через обозначено количество элементов, принадлежащих множеству F).

Заметим, что 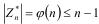. Таким образом, если тест Ферма выявляет составное n при одном основании a, то существует не менее оснований с аналогичным свойством.

Действительно, свойство а) следует из определения ord_na. Свойства б) и в) следуют из правила почленного перемножения частей сравнений и проверки сравнения Ферма для основания .

Докажем свойство г). Пусть и a – основание, по которому n не является псевдопростым. Тогда для любого i пара чисел 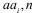не удовлетворяет сравнению Ферма. Поэтому количество оснований, для которых n не является псевдопростым, не меньше, чем количество элементов в F_n

Следовательно, если 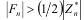, то общее число элементов в 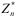окажется больше n, что невозможно.

Таким образом, можно заключить, что если существует (даже не известное нам) основание, по которому n не является псевдопростым, то, при повторении теста Ферма k раз, вероятность k -кратного выбора оснований из множества F не превосходит . В этом случае вероятность ошибки теста стремится к нулю с увеличением k.

Проблема может возникнуть лишь в том случае, если n является псевдопростым для всех (ненулевых) оснований. Оказывается, такие числа существуют. Они называются числами Кармайкла. Например, числом Кармайкла является число (48).

Свойства чисел Кармайкла описываются следующей теоремой.

Теорема (Кармайкл). Пусть n – нечетное составное число. Тогда

1) если 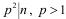, то n не является числом Кармайкла;

2) если 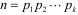, для , то n – число Кармайкла в том и только том случае, когда ;

3) если , для 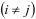– число Кармайкла, то .

Числа Кармайкла являются достаточно редкими. В пределах до 100000 существует лишь 16 чисел Кармайкла: 561, 1105, 1729, 2465, 2821, 6601, 8911, 10585, 15841, 29341, 41041, 46657 52633, 62745, 63973, 75361 (49).

6. Тест Соловея-Штрассена и Эйлеровы псевдопростые числа

Из предыдущего следует, что при тестировании чисел на простоту с помощью вероятностного теста, основанного на малой теореме Ферма, может возникнуть ситуация, когда вероятность ошибки не снижается с количеством повторений теста.

В подобном случае упомянутая вероятность равна единице и в результате тестирования может быть принято неверное решение.

В этой связи, разработаны и применяются на практике вероятностные тесты, свободные от указанного недостатка.

Примерами таких тестов являются тест Соловея-Штрассена и тест Рабина-Миллера проверки чисел на простоту.

В тесте Соловея-Штрассена используются свойства символов Лежандра и Якоби, связанных с разрешимостью двучленных квадратичных сравнений. Напомним вкратце их свойства.

Двучленным квадратичным сравнением называется сравнение вида 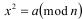(50), где x - неизвестный вычет.

Целое число a называется квадратичным вычетом по модулю n, если сравнение 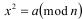(50) разрешимо. Если сравнение разрешимо, то для составного нечетного модуля количество решений, как правило, больше двух.

В общем случае, не только решение квадратичных сравнений, но даже вопрос о разрешимости двучленного квадратичного сравнения по составному модулю, факторизация которого неизвестна, является алгоритмической проблемой, на сложности которой основан ряд криптопротоколов и криптосистем.

В то же время для модулей, являющихся простыми числами, задача легко поддается анализу.

Существует эффективный алгоритм для определения, является ли данное число квадратичным вычетом по простому нечетному модулю p или нет. Этот алгоритм позволяет вычислить, практически вручную, символ Лежандра (51), значение которого при 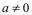равно 1, если a - квадратичный вычет, и (-1) – в противном случае. Для полагается (51а).

С появлением компьютеров значение обычно вычисляется, исходя из соотношения: (51б), которое является важным свойством символа Лежандра.

Если нечетное число n факторизовано: , то разрешимость сравнения эквивалентна разрешимости всех сравнений вида (51в).

Заметим, что, в свою очередь, сравнение разрешимо тогда и только тогда, когда 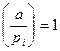, а также, произведение двух квадратичных невычетов является квадратичным вычетом по простому модулю.

Поэтому значение можно вычислить через величины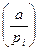

С символом Лежандра тесно связан символ Якоби числа x по модулю n. Символ Якоби определяется для нечетных, взаимно простых чисел как произведение значений символов Лежандра: (52).

Он обладает практически всеми теми же свойствами, что и символ Лежандра, но по значению символа Якоби равному единице, нельзя утверждать, что соответствующий вычет x – квадратичный. Для квадратичного вычета, тем не менее, символ Якоби равен единице. Следовательно, если , то x - квадратичный невычет по модулю n.

Эта особенность связана с тем, что соотношение 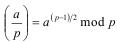(51б) не обязательно выполняется для символа Якоби, т.е, когда число p (модуль) не является простым. Для нас символ Якоби важен потому, что его можно вычислить без факторизации модуля.

На основании следующей теоремы, в тесте Соловея-Штрассена используется критерий Эйлера для определения значения символа Лежандра (квадратичного характера числа по простому модулю). В самом тесте при тестировании числа n вычисляется символ Якоби .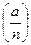

Теорема. Нечетное целое число n > 1 является простым тогда и только тогда, когда для всех чисел 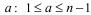выполняется соотношение Эйлера: .

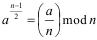Составное число n, удовлетворяющее соотношению Эйлера, называется эйлеровым псевдопростым по основанию a.

Из указанной теоремы следует, что составных чисел, которые были бы эйлеровыми псевдопростыми по любому основанию, не существует.

Следовательно, мы можем предложить следующий тест, аналогичный тесту Ферма.

Псевдослучайно выбираем вычет и проверяем условие . Если условие не выполнено, значит, n – составное.

Проверяем соотношение Эйлера. Если оно не выполняется, то число n – составное. Иначе, повторяем тест для другого значения a.

Если мы могли бы проверить соотношение Эйлера для всех значений a, то мы смогли бы точно определить, является ли число n простым.

Но для больших n это невозможно. Поэтому необходимо оценить, как ведет себя вероятность ошибки при увеличении числа k повторений теста.

Это можно сделать, исходя из утверждения, аналогичного тому, которое мы рассматривали при анализе свойств псевдопростых чисел.

Интересно, что эйлеровы псевдопростые являются псевдопростыми числами.

Теорема. Пусть n – нечетное составное число. Тогда:

а) если n – эйлерово псевдопростое по основанию a, то оно – псевдопростое по основанию a;

б) если n – эйлерово псевдопростое по основаниям a и b, то n – эйлерово псевдопростое по основаниям ab и ab^-1(modn);

в) множество: является подгруппой группы ; 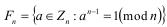

г) если n не является эйлеровым псевдопростым по основанию a, хотя бы для одного числа a, то .

Таким образом, при повторении теста Соловея-Штрассена k раз, вероятность неотбраковки составного числа не превосходит 

7. Тест Рабина-Миллера и сильные псевдопростые числа

Еще более эффективным вероятностным тестом является тест Рабина-Миллера, в котором используется критерий, в конечном счете, основаный на факте, что для простого модуля квадратными корнями из единицы являются лишь числа 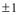а для составного нечетного модуля , 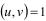число таких корней больше двух.

Пусть n – нечетное натуральное число. Тогда можно записать , где t – нечетное и .

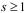Если число n – простое, то , при 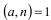. Поэтому квадратные корни из единицы имеют вид: 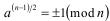, где показатель равен .

Это означает, что в последовательности 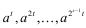вычетов по простому модулю n, которые являются последовательными квадратами числа a^t, либо появится 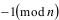, либо все эти вычеты сравнимы с единицей, т.е. 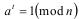. Заметим, что при простом n, левее могут располагаться лишь вычеты не равные .

Если n – составное, то возможны и другие варианты, поскольку в этом случае, кроме , существуют другие корни из единицы по модулю n.

Основанный на данном замечании тест Рабина-Миллера заключается в следующем:

1) псевдослучайно выбираем вычет и проверяем условие . Если условие не выполнено, значит, n – составное и работа закончена;

2) вычисляем . Если 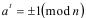, то не исключено, что число n – простое и необходимо перейти на начало, чтобы повторить тест для другого основания;

3) вычисляем последовательно вычеты чисел , по модулю n, пока не появится (- 1), либо не исчерпается список;

4) если (- 1) обнаружена в списке, то не исключено, что число n – простое и необходимо перейти на начало, чтобы повторить тест для другого основания;

5) если ни одно число из списка не сравнимо с (- 1), то число n – составное и необходимо закончить работу.

Как и для других вероятностных тестов, существуют составные числа n, которые, для соответствующих оснований a, проходят данный тест.

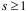Назовем число , где , t – нечетно, сильным псевдопростым по основанию , если выполняется одно из двух условий: , либо в последовательности существует число, сравнимое с –1 по модулю n.

Оказывается, можно показать, что для любого a, (a,n) = 1, существует бесконечно много сильных псевдопростых чисел n по основанию a.

Примеры: a = 7, n = 25; a = 5, n = 781.

Можно доказать следующие основные свойства сильных псевдопростых чисел:

1) число n, сильное псевдопростое по основанию a, является эйлеровым псевдопростым по тому же основанию;

2) если нечетное составное число n является сильным псевдопростым по основанию a, то общее количество оснований, по которому это число является сильным псевдопростым, не превышает .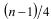

Поэтому можно утверждать, что при повторении испытаний теста Рабина-Миллера k раз, вероятность неотбраковки составного числа .

Кроме того, оказывается, количество повторений теста, достаточное для практических приложений, можно ограничить величиной .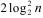

Интересно отметить, что простоту небольших простых чисел можно доказать, используя несколько заранее указанных оснований.

Пример: если n < 1373653 – сильное псевдопростое по основаниям 2 и 3, то n – простое; если n < 341550071728321 – сильное псевдопростое по основаниям 2, 3, 5, 7, 11, 13, 17, то n – простое.

8. Общие требования к выбору параметров RSA

Корректность параметров RSA связана с оценкой стойкости системы и может быть определена лишь с точки зрения практической стойкости.

Следовательно, корректные параметры должны быть построены так, чтобы минимизировать ущерб от известных подходов к ослаблению криптосистемы.

Исходя из этих соображений, рассмотрим наиболее общие требования к выбору параметров p,q,e,d криптосистемы RSA.

Прежде всего, следует учитывать, что слабость одного из параметров практически не компенсируется усилением свойств других параметров.

Очевидно, число n = pq должно быть большим (1). Числа p и q не должны содержаться в списках известных больших простых чисел, не должны быть слишком близки друг к другу, либо существенно различаться по величине (2).

Они не должны быть построенными по детерминированным алгоритмам с небольшим числом известных вариантов начальных параметров или содержать закономерности в двоичной записи (3).

В общем, p и q не должны отличаться от типичных представителей случайных простых чисел (4). Аналогичными свойствами должны обладать параметры e и d.

Например, если секретный ключ d содержит в двоичной записи небольшое количество единиц, то номера мест этих единиц легко определить перебором.

Можно доказать, что при известном d существует возможность факторизации модуля.

Известно, что для чтения сообщений, зашифрованных криптосистемой RSA, достаточно знания некоторого кратного функции Эйлера от модуля, т.к. в этом случае можно вычислить ключ, криптоэквивалентный ключу d.

Заметим также, что при наличии ord_na легко получить a из сравнения . Достаточно возвести c в степень h, удовлетворяющую соотношению .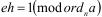

Далее. Для любого a, взаимно простого с 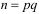, делит , а делит . Поэтому ord_na делит .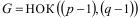

Следовательно, для построения криптосистемы, вместо определения d из сравнения , можно воспользоваться решением сравнения .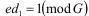

Пусть 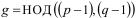. Тогда .

Очевидно, из соотношения 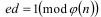следует 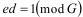, поэтому 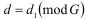и .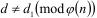

Этим условиям удовлетворяют ключи d₁, d₁ + G, d₁ + 2G,…,d₁ + (g - 1)G, криптоэквивалентные, таким образом, ключу d. Следовательно, чем больше , тем больше криптоэквивалентных ключей, тем хуже для криптосистемы.

Очевидно, в наилучшем возможном случае, , при этом, 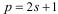, , где , скажем, s и t – простые.

Заметим, кстати, что неизвестно, является ли множество простых чисел вида 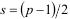бесконечным.

Оказывается, чтобы исключить возможность применения большинства частных методов факторизации для дешифрования криптосистемы RSA, достаточно потребовать, чтобы числа , , 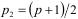и 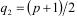не разлагались в произведение степеней небольших простых чисел, т.е. чтобы они содержали в разложении большое простое число.

Соответствующие требования, в наиболее сильной форме, заключаются в том, чтобы числа p₁,p₂,q₁,q₂ были простыми, более того, требуется, чтобы в разложении как p - 1, так и q₁ – 1 содержалось большое простое число.

На практике, при построении соответствующего этим требованиям простого числа, скажем, p, достаточно, чтобы существовал достаточно большой простой делитель числа . Очевидно, такой делитель имеет вид .

Таким образом, необходимо выделить некоторый специфический класс простых чисел.

Определение. Простое число p называется сильным простым, если выполняются условия:

,

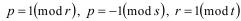где r,s,t – большие простые числа.

Поскольку числа p,r,s,t – нечетные, то они представляются в виде , , 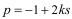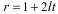. Кроме того, для наших целей, чем меньше числа j,k,l, тем лучше.

Для построения сильных простых чисел применяется т.н. метод Гордона.

В этом методе осуществляется просмотр окрестностей некоторых псевдослучайных чисел с целью обнаружения простых чисел, удовлетворяющих специфическим условиям.

При этом неоднократно используются вероятностные процедуры построения промежуточных данных, а также применяется тестирование чисел на простоту с помощью теста Рабина-Миллера.

9. Метод Гордона построения сильных простых чисел

Суть метода Гордона построения сильного простого числа

Дата добавления: 2014-10-10; просмотров: 1033; Нарушение авторских прав

Мы поможем в написании ваших работ!