
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
Упорядоченное поле
Поле
О. Непустое множество  с двумя алгебраическими операциями сложением (+) и умножением (·) называется полем, если
с двумя алгебраическими операциями сложением (+) и умножением (·) называется полем, если  является коммутативным кольцом с единицей, причем нулевой элемент и единичный элемент не совпадают, для каждого элемента
является коммутативным кольцом с единицей, причем нулевой элемент и единичный элемент не совпадают, для каждого элемента  существует в
существует в  обратный ему элемент
обратный ему элемент 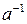 .
.
Отметим некоторые свойства поля.
1) Для любых элементов  и
и  из
из  , где
, где  , в поле разрешимо уравнение
, в поле разрешимо уравнение 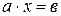 .
.
Д. Существует 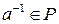 , тогда
, тогда 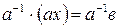 или
или 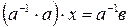 . Тогда
. Тогда 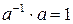 , то
, то 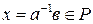 .
.
2) В поле нет делителей нуля, т.е. из 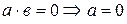 или
или 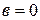 .
.
Д. Пусть  , тогда
, тогда 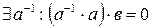 или
или 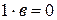 , но
, но 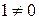 , стало быть
, стало быть 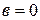 .
.
3) Множество 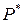 ненулевых элементов поля
ненулевых элементов поля  образует группу по умножению (непосредственно следует из определения поля).
образует группу по умножению (непосредственно следует из определения поля).
4) По определению всякое поле является кольцом, но не всякое кольцо является полем. Например, кольцо целых чисел не является полем (почему?).
Упр. 22. Докажите, что множество классов вычетов по модулю 5, т.е. 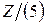 , является полем, а по модулю 6
, является полем, а по модулю 6 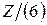 не является полем.
не является полем.
О. Поле  называется упорядоченным, если на нем определено отношение порядка, т.е. отношение, обладающее свойствами транзитивности, антисимметричности и связности, обозначаемое символом “<” (“>”). При этом, если
называется упорядоченным, если на нем определено отношение порядка, т.е. отношение, обладающее свойствами транзитивности, антисимметричности и связности, обозначаемое символом “<” (“>”). При этом, если 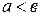 , то говорят, что «а меньше в» или «а предшествует в», и выполняются следующие свойства:
, то говорят, что «а меньше в» или «а предшествует в», и выполняются следующие свойства:
1) для любых 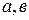 и
и 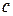 из
из  если
если 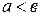 , то
, то 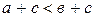 (монотонность сложения);
(монотонность сложения);
2) для любых 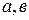 и
и 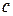 из
из  если
если 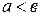 и
и 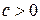 , то
, то 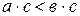 (монотонность умножения);
(монотонность умножения);
3) для любого  из
из  , где
, где  , следует, что
, следует, что 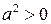 , т.е. квадрат любого элемента положителен.
, т.е. квадрат любого элемента положителен.
Упр. 23. Докажите, что в упорядоченном поле, если 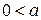 , то
, то  .
.
| <== предыдущая страница | | | следующая страница ==> |
| Кольцо с делителями нуля | | | Поле рациональных чисел |
Дата добавления: 2014-03-11; просмотров: 272; Нарушение авторских прав

Мы поможем в написании ваших работ!