Теоремы умножения вероятностей (для зависимых и независимых событий)

Вероятность совместного наступления двух зависимых событий равна произведению вероятности одного из них на условную вероятность другого, вычисленную в предположении, что первое событие уже наступило, то есть

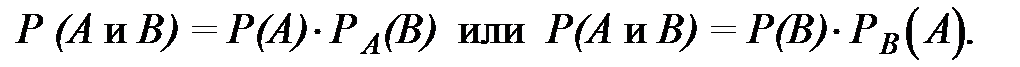
Доказательство. Пусть события А и В зависимые. N - число всех равновозможных, единственно возможных и несовместных исходов. Из них М - число исходов, благоприятствующих событию А. Тогда 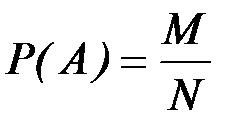. Событию В благоприятствует 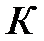исходов из М, поэтому .

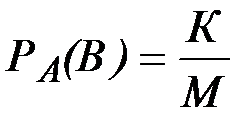Совместному наступлению событий А и В благоприятствуют К исходов из N, следовательно, Р(А и В) = 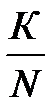. Умножим числитель и знаменатель этой дроби на М, получим

Р (А и В) = = = ,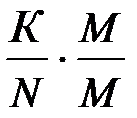

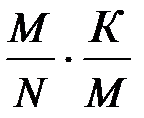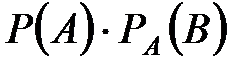что и требовалось доказать.

Теорема. Вероятность совместного наступления конечного числа зависимых событий равна произведению вероятности одного из них на условные вероятности всех остальных, причем условная вероятность каждого последующего события вычислена в предположении, что все предыдущие уже наступили, то есть

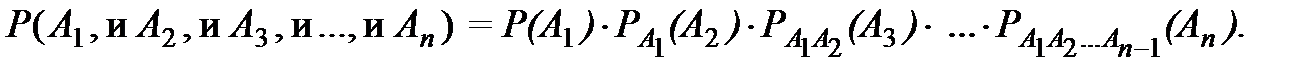
Доказательство. Докажем теорему методом математической индукции. Для двух событий теорема доказана. Предположим, что она справедлива для (n-1) событий, то есть

P(А₁, и А₂, и А_n, и …, и А_n-1)= .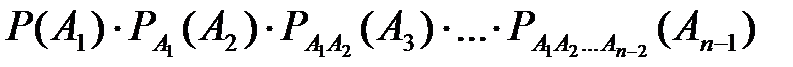

Обозначим событие (А₁, и А₂, и А₃, и, …, и А_n-1) через В. Найдем вероятность совместного наступления событий В и А_n, применяя теорему умножения вероятностей для двух событий

= .

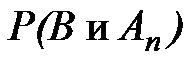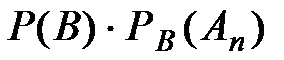Так как, по предположению, вероятность события В равна вероятности совместного наступления (n-1) событий, то

P(А₁, и А₂, и А₃, и …, и А_n-1, и А_n)=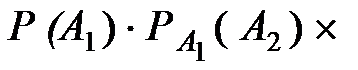

.

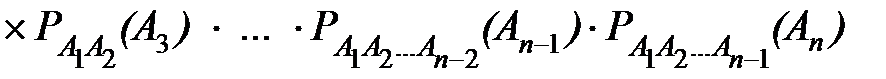Замечание. Расположение входящих в произведение событий не играет роли. Для трех событий формула примет вид

Р(А, и В, и С) =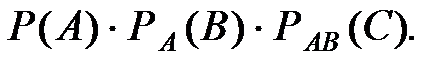

Ранее было отмечено, что если события независимые, то их условные вероятности равны безусловным. Тогда теорема умножения вероятностей для независимых событий может быть сформулирована так.

Теорема.Вероятность совместного наступления конечного числа независимых событий равна произведению вероятностей этих событий, то есть

Р (А₁, и А₂, и А₃, и ..., и А_n) = .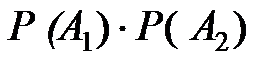

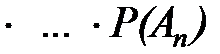1.6 Формула полной вероятности

Теорема.Вероятность события В, которое может наступить только с одним из событий А₁, А₂, ... , А_n, образующих полную группу событий, равна сумме произведений вероятностей каждого из событий А_i на соответствующую условную вероятность события В, то есть

.

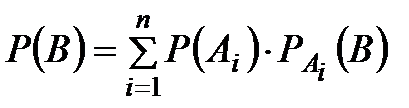Доказательство. По условию теоремы событие В может наступить только с одним из событий А₁, А₂, ... , А_n. Это означает, что появление события В равносильно появлению одного из событий: (А₁ и В), или (А₂ и В), или ..., или (А_n и В). Так как события А₁, А₂, ..., А_n несовместны, то и события (А₁ и В), (А₂ и В), ..., (А_n и В) также несовместны. Применяя теорему сложения вероятностей для несовместных событий, а затем теорему умножения вероятностей, получим

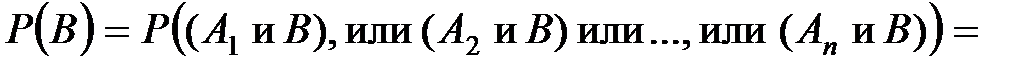
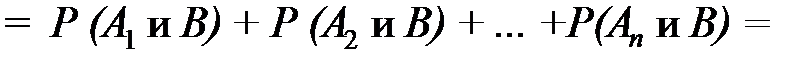
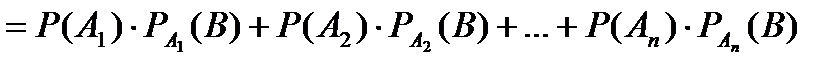
или ,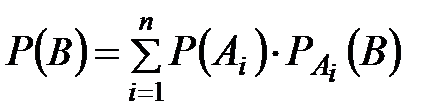

что и требовалось доказать.

Полученная формула называется формулой полной вероятности, а события А₁ , А₂ , ..., А_n - гипотезами.

Дата добавления: 2014-09-01; просмотров: 1025; Нарушение авторских прав

Мы поможем в написании ваших работ!