Дифференциальная форма теоремы о циркуляции

Предположим, что ток течет не по отдельным проводам, а распределен в пр-ве непрерывным образом с плотностью .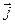

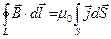
По теореме Стокса: => =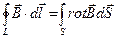

=> =

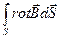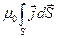
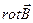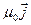
это и есть дифференциальная форма теоремы о циркуляции.

Потоком вектора 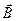через какую-либо поверхность S называется интеграл:

,

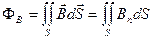где 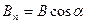- проекция вектора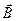на нормаль к поверхности S в данной точке (рис.10.1).

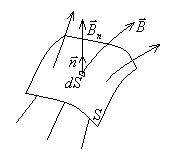
Рис.10.1. К определению потока вектора магнитной индукции.

Прежде чем сформулировать теорему Гаусса в магнитостатике, вспомним, что в электростатике аналогичная теорема формулировалась как:

,

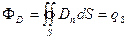где интеграл берется по замкнутой поверхности S, окружающей электрические заряды (q_s – алгебраическая сумма зарядов, заключенных под этой поверхностью); 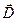- вектор электрической индукции ( в вакууме).

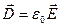Казалось бы, что в полной аналогии с электростатикой мы могли бы написать:

,

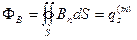подразумевая под 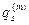алгебраическую сумму неких «магнитных зарядов», охваченных замкнутой поверхностью S, и являющихся источниками магнитных полей с результирующей индукцией 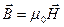(в вакууме).

Но, как оказалось, в природе нет магнитных зарядов, подобных электрическим, а источниками магнитных полей являются движущиеся заряды, то есть электрические токи. Следует, однако, заметить, что законы классической электродинамики допускают существование частиц с одним магнитным полюсом – магнитных монополей. В квантовой механике магнитный монополь – это стабильная частица, несущая положительный или отрицательный магнитный заряд, величина которого значительно превосходит величину элементарного электрического заряда. Впервые гипотезу о существовании магнитного монополя высказал в 1931г. один из основателей квантовой механики Поль Дирак (Dirac P., 1902-1984), поэтому эту частицу называют также монополем Дирака. Тщательные поиски монополя Дирака не увенчались успехом, поэтому вопрос о их существовании остается пока открытым.

Полагая, таким образом, что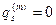, приходим к следующей формулировке теоремы Гаусса в магнитостатике:

.

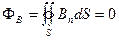Равенство нулю потока магнитной индукции через произвольную замкнутую поверхность означает, что силовые линии магнитного поля нигде не обрываются и, следовательно, являются замкнутыми (рис.10.2).

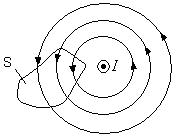
Рис.10.2. К формулировке теоремы Гаусса в магнитостатике.

Поля, силовые линии которых замкнуты, называются вихревыми или соленоидальными.

Дата добавления: 2014-02-26; просмотров: 762; Нарушение авторских прав

Мы поможем в написании ваших работ!