
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
Магнитное поле соленоида и тороида
Применим полученные результаты для нахождения напряженности магнитного поля на оси прямого длинного соленоида и тороида.
1) Магнитное поле на оси прямого длинного соленоида.
Соленоидпредставляет собой катушку, намотанную на цилиндрический каркас. Если длинасоленоида много больше его диаметра, то такой соленоид называют длинным (в отличие от короткой катушки с противоположным соотношением размеров). Магнитное поле максимально внутри соленоида и направлено вдоль его оси. Вблизи оси соленоида магнитное поле можно считать однородным.
Для нахождения напряженности магнитного поля на оси прямого длинного соленоида с помощью теоремы о циркуляции магнитного поля, выберем контур интегрирования, как показано на рис.10.5.
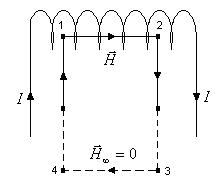
Рис.10.5. К расчету напряженности магнитного поля на оси соленоида.
На участке 1-2 направление магнитного поля совпадает с направлением обхода контура, а его напряженность постоянна в силу однородности поля. На участках 2-3 и 4-1 вне соленоида проекция магнитного поля на направление обхода равна нулю. Наконец, на участке 3-4, удаленном достаточно далеко от соленоида, можно считать, что магнитное поле отсутствует.
С учетом сказанного имеем:
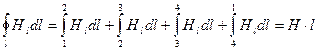 ,
,
где
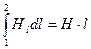 ,
, 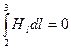 ,
, 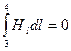 ,
, 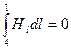 .
.
Но согласно теореме о магнитном напряжении этот интеграл равен 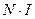 , где N – число витков соленоида, сцепленных с контуром интегрирования. Следовательно
, где N – число витков соленоида, сцепленных с контуром интегрирования. Следовательно
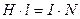 ,
,
откуда находим: 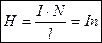 ,
,
где через 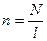 обозначено число витков на единицу длины соленоида.
обозначено число витков на единицу длины соленоида.
2) Магнитное поле на оси тороида.
Тороидпредставляет собой катушку, намотанную на каркас, имеющий форму тора. Магнитное поле тороида целиком сосредоточено внутри него и является неоднородным. Максимальное значение напряженность магнитного поля имеет на оси тороида.
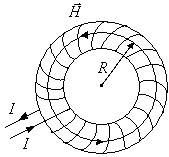
Рис.10.6. К расчету напряженности магнитного поля на оси тороида.
Для нахождения напряженности магнитного поля вблизи оси тороида применим теорему о циркуляции магнитного поля, выбрав контур интегрирования, как показано на рис.10.6.
Имеем:
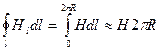 .
.
С другой стороны, этот интеграл равен 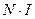 , откуда следует, что
, откуда следует, что
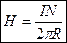 .
.
| <== предыдущая страница | | | следующая страница ==> |
| Дифференциальная форма теоремы о циркуляции | | | Изменчивость и ее формы |
Дата добавления: 2014-02-26; просмотров: 762; Нарушение авторских прав

Мы поможем в написании ваших работ!