
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
РАЗДЕЛ IV. МАГНИТНОЕ ПОЛЕ
Основные формулы для решения задач
1. Индукция магнитного поля
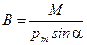 ,
,
где M - величина момента сил, действующего на плоский проводящий замкнутый контур с током, помещенный в однородное магнитное поле; 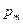 - магнитный момент контура; a - угол между векторами
- магнитный момент контура; a - угол между векторами 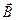 и
и 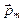 .
.
2. Закон Био-Савара-Лапласа:
 или
или 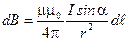 ,
,
где 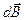 - магнитная индукция поля, создаваемого элементом проводника длиной
- магнитная индукция поля, создаваемого элементом проводника длиной 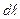 с током I;
с током I;  - радиус-вектор, направленный от элемента к точке, в которой магнитная индукция вычисляется; a - угол между радиус-вектором и направлением тока в элементе проводника; m - магнитная проницаемость;
- радиус-вектор, направленный от элемента к точке, в которой магнитная индукция вычисляется; a - угол между радиус-вектором и направлением тока в элементе проводника; m - магнитная проницаемость; 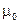 - магнитная постоянная.
- магнитная постоянная.
3. Магнитная индукция в центре кругового тока
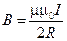 ,
,
где R - радиус кругового витка.
4. Магнитная индукция на оси кругового тока
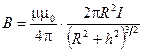 ,
,
где h - расстояние от центра витка до точки на оси кругового тока, в которой вычисляется магнитная индукция.
5. Магнитная индукция поля бесконечного прямого тока
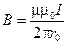 ,
,
где 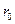 - расстояние от оси проводника до точки, в которой вычисляется магнитная индукция.
- расстояние от оси проводника до точки, в которой вычисляется магнитная индукция.
6. Магнитная индукция поля, создаваемого конечным проводником с током в произвольной точке
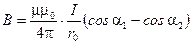 ,
,
где 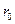 - расстояние от произвольной точки до линии тока;
- расстояние от произвольной точки до линии тока; 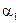 и
и 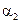 - углы, образованные радиус-векторами, проведенными в точку из начала и конца проводника, с направлением тока.
- углы, образованные радиус-векторами, проведенными в точку из начала и конца проводника, с направлением тока.
7. Магнитная индукция поля длинного соленоида
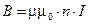 ,
,
где n - число витков соленоида, приходящихся на единицу длины  .
.
8. Сила Ампера (сила, действующая на проводник с током в магнитном поле)
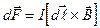 ,
,
где 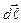 - вектор, численно равный длине
- вектор, численно равный длине 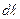 элемента проводника, совпадающий по направлению с током.
элемента проводника, совпадающий по направлению с током.
Если проводник прямой и поле однородное
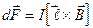 или
или 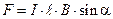 ,
,
где 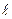 - длина проводника, a - угол между направлением тока и вектором индукции магнитного поля.
- длина проводника, a - угол между направлением тока и вектором индукции магнитного поля.
9. Сила взаимодействия параллельных токов (сила, действующая на участок проводника длиной 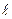 )
)
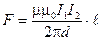 ,
,
где d - расстояние между проводниками.
10. Магнитный момент контура с током
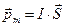 ,
,
где I - сила тока, 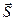 - вектор, численно равный площади, охватываемой контуром и направленный по нормали к плоскости контура. Направление нормали и тока связаны правилом правого буравчика.
- вектор, численно равный площади, охватываемой контуром и направленный по нормали к плоскости контура. Направление нормали и тока связаны правилом правого буравчика.
11. Механический момент, действующий на контур с током, помещенный в однородное магнитное поле
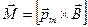 или
или 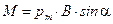 ,
,
где a - угол между векторами 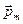 и
и 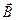 .
.
12. Потенциальная энергия контура с током в магнитном поле:
 или
или 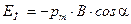 .
.
За нулевое значение  принято положение контура, при котором вектор
принято положение контура, при котором вектор 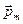 перпендикулярен вектору
перпендикулярен вектору 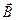 .
.
13. Напряженность магнитного поля
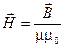 .
.
14. Принцип суперпозиции магнитных полей:
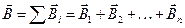 ,
,
где 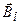 - индукция магнитного поля, создаваемая в данной точке поля i-м источником (током) магнитного поля.
- индукция магнитного поля, создаваемая в данной точке поля i-м источником (током) магнитного поля.
15. Сила Лоренца
 или
или 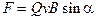 ,
,
где Q - заряд частицы (в формуле необходимо учитывать знак заряда); v - скорость заряженной частицы; a - угол между векторами 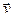 и
и 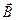 .
.
16. Магнитный поток:
а) в случае однородного магнитного поля и плоской поверхности
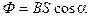 или
или 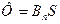 ,
,
где S - площадь охватываемая контуров; a - угол между нормалью к плоскости контура и вектором магнитной индукции;
б) в случае неоднородного поля и произвольной поверхности
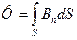 ,
,
интегрирование ведется по всей поверхности (поверхность опирается на контур).
17. Потокосцепление (полный поток)
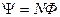 .
.
Эта формула верна для соленоида и тороида с равномерной намоткой плотно прилегающих друг к другу N витков.
18. Работа по перемещению замкнутого контура в магнитном поле
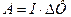 .
.
19. Электромагнитная индукция. Явление электромагнитной индукции состоит в том, что при всяком изменении магнитного потока, сцепленного с контуром (потокосцепления), в контуре возникает ЭДС индукции.
Абсолютная величина ЭДС индукции (в системе единиц СИ) равна абсолютной величине скорости изменения магнитного потока, сцепленного с контуром
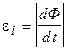 .
.
Если проводящий контур замкнут, то ЭДС индукции вызывает в нем индукционный ток. Изменение магнитного потока, сцепленного с контуром, может быть обусловлено:
- изменением пронизывающего контур магнитного поля;
- изменением формы контура;
- изменением положения контура в магнитном поле.
Э.Х.Ленц установил закон, согласно которому индукционный ток всегда имеет такое направление, что создаваемый им магнитный поток сквозь поверхность, опирающуюся на контур, противодействует изменениям того магнитного потока, которые вызывают этот индукционный ток. Закон Ленца в формуле для ЭДС индукции отражен знаком «-»:
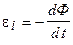 . (19.1)
. (19.1)
20. Разность потенциалов на концах проводника, движущегося со скоростью 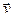 в магнитном поле
в магнитном поле
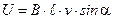 ,
,
где 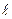 - длина проводника; a - угол между векторами
- длина проводника; a - угол между векторами 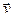 и
и 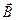 .
.
21. Заряд, протекающий по замкнутому контуру при изменении магнитного потока, пронизывающего этот контур
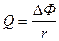 или
или 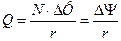 ,
,
где r - сопротивление контура.
22. Индуктивность контура
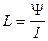 .
.
23. Э.Д.С. самоиндукции
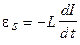 .
.
24. Индуктивность соленоида
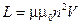 ,
,
где n - число витков, приходящееся на единицу длины соленоида; V - объем соленоида.
25. Мгновенное значение силы тока в цепи, обладающей сопротивлением r и индуктивностью L:
а) при замыкании цепи (ЭДС включается в цепь содержащую катушку индуктивности)
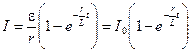 ,
,
где e - ЭДС источника тока; r – электрическое сопротивление цепи; 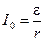 - установившийся ток в цепи; t - время, прошедшее после замыкания цепи.
- установившийся ток в цепи; t - время, прошедшее после замыкания цепи.
б) при размыкании цепи
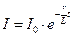 ,
,
где 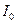 - значение силы тока в цепи в начальный момент времени, при
- значение силы тока в цепи в начальный момент времени, при 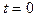 ; t - время, прошедшее с момента размыкания цепи.
; t - время, прошедшее с момента размыкания цепи.
26. Энергия магнитного поля контура (соленоида, катушки и т.д.) с током
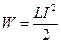 .
.
27. Объемная плотность энергии магнитного поля (энергия, заключенная в единице объема):
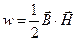 ;
;
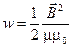 ;
;
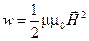 ,
,
где 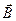 - магнитная индукция;
- магнитная индукция; 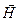 - напряженность магнитного поля.
- напряженность магнитного поля.
Примеры решения задач
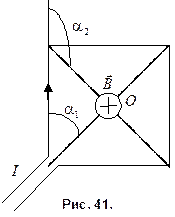 Пример 1. По проводу, согнутому в виде квадрата со стороной
Пример 1. По проводу, согнутому в виде квадрата со стороной 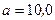 см, течет ток силой
см, течет ток силой  А. Найти магнитную индукцию
А. Найти магнитную индукцию 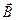 в точке О пересечения диагоналей квадрата.
в точке О пересечения диагоналей квадрата.
Решение. Сделаем рисунок (рис. 41). Расположим квадратный виток в плоскости чертежа. В точке О определим с помощью правила правого буравчика (векторного произведения) направления 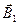 ,
,  ,
, 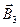 и
и 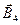 , создаваемые токами, протекающими по каждой стороне квадрата.
, создаваемые токами, протекающими по каждой стороне квадрата.
1. Согласно принципа суперпозиции полей, результирующее поле в точке О
 .
.
В точке О все векторы индукции направлены перпендикулярно плоскости витка («от нас»).
Из симметрии следует, что модули этих векторов одинаковы 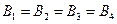 . Следовательно,
. Следовательно, 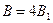 .
.
2. Индукция магнитного поля, создаваемого отрезком прямолинейного провода с током, выражается формулой
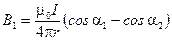 ,
,
где 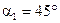 ,
, 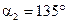 ,
, 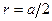 .
.
3. Получим расчетную формулу для первого элемента контура
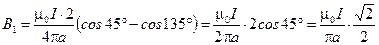 .
.
4. Результирующая индукция в центре квадрата равна
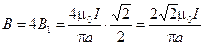 .
.
5. Проведем вычисление
 мТл.
мТл.
Ответ: 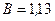 мТл.
мТл.
 Пример 2. С какой силой действует магнитное поле постоянного электрического тока силой
Пример 2. С какой силой действует магнитное поле постоянного электрического тока силой 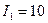 А, текущего по прямолинейному бесконечно длинному проводнику, на контур из провода, изогнутого в виде квадрата? Проводник расположен в плоскости контура параллельно двум его сторонам. Длина стороны контура
А, текущего по прямолинейному бесконечно длинному проводнику, на контур из провода, изогнутого в виде квадрата? Проводник расположен в плоскости контура параллельно двум его сторонам. Длина стороны контура 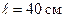 , сила тока в нем
, сила тока в нем 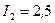 А. Расстояние от прямолинейного тока до ближайшей стороны контура
А. Расстояние от прямолинейного тока до ближайшей стороны контура 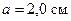 .
.
Решение. Сделаем рисунок (рис. 42). Квадратная рамка с током находится в неоднородном магнитном поле прямого тока. Индукция магнитного поля бесконечного прямого тока
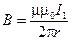 , (1)
, (1)
где r - кратчайшее расстояние от оси проводника до точки, в которой рассчитывается B.
1. Вектор 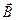 во всех точках рамки направлен перпендикулярно к плоскости рамки. Каждая из сторон рамки - прямолинейный проводник. Поэтому в пределах одной стороны все элементарные силы параллельны друг другу.
во всех точках рамки направлен перпендикулярно к плоскости рамки. Каждая из сторон рамки - прямолинейный проводник. Поэтому в пределах одной стороны все элементарные силы параллельны друг другу.
2. Стороны контура 2 и 4 одинаково расположены по отношению к прямолинейному проводнику, но направления тока в них противоположны, поэтому
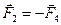 .
.
Результирующая этих сил равна нулю.
3. Стороны контура 1 и 3 параллельны прямому току и находятся от него на расстояниях соответственно 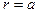 и
и 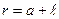 . Силы
. Силы 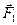 и
и 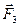 направлены в противоположные стороны. Поэтому результирующая сила
направлены в противоположные стороны. Поэтому результирующая сила
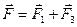 ,
,
ее модуль
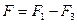 .
.
4. Подставив выражения для r в формулу (1) и учитывая закон Ампера, получим:
для первого элемента контура 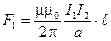 ;
;
для третьего элемента контура 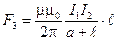 .
.
5. Получим расчетную формулу для результирующей силы действующей на контур
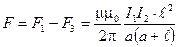 .
.
6. Выполним расчеты
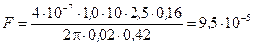 Н.
Н.
Ответ: 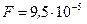 Н.
Н.
 Пример 3. Плоский квадратный контур со стороной
Пример 3. Плоский квадратный контур со стороной 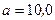 см, по которому течет ток силой
см, по которому течет ток силой 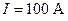 , свободно установился в однородном магнитном поле (
, свободно установился в однородном магнитном поле ( 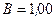 Тл). Определить работу A, совершаемую внешними силами при повороте контура относительно оси, проходящей через середину его противоположных сторон, на угол
Тл). Определить работу A, совершаемую внешними силами при повороте контура относительно оси, проходящей через середину его противоположных сторон, на угол 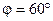 . При повороте контура сила тока в нем поддерживается неизменной.
. При повороте контура сила тока в нем поддерживается неизменной.
Решение. Изобразим контур с током в магнитном поле (рис. 43).
1. На контур с током в магнитном поле действуют силы Ампера, которые в данном случае образуют вращающую пару сил.
2. Вращающий момент пары сил по определению есть произведение плеча на силу и синус угла между ними:
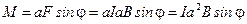 .
.
3. С другой стороны можно записать
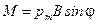 ,
,
где 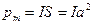 - магнитный момент контура; j - угол между векторами
- магнитный момент контура; j - угол между векторами 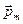 и
и 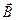 .
.
4. В начальном положении контур свободно установился в магнитном поле. При этом вращающий момент равен нулю 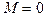 , а, значит,
, а, значит, 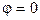 , т.е. векторы
, т.е. векторы 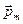 и
и 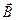 совпадают по направлению. Если внешние силы выводят контур с током из положения равновесия, то возникает момент сил, стремящийся возвратить контур в исходное положение - положение устойчивого равновесия. Против этого момента и будет совершаться работа внешних сил. Так как момент сил переменный (зависит от угла поворота j), то для подсчета работы применим формулу для работы при вращательном движении в дифференциальной форме
совпадают по направлению. Если внешние силы выводят контур с током из положения равновесия, то возникает момент сил, стремящийся возвратить контур в исходное положение - положение устойчивого равновесия. Против этого момента и будет совершаться работа внешних сил. Так как момент сил переменный (зависит от угла поворота j), то для подсчета работы применим формулу для работы при вращательном движении в дифференциальной форме
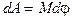 .
.
Подставляя сюда выражение для M, получаем
 .
.
Возьмем интеграл от этого выражения и найдем работу при повороте контура на любой конечный угол
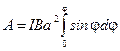 .
.
5. Работа магнитного поля при повороте на угол 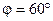
 .
.
6. Выразим численные значения в единицах СИ: 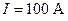 ;
;  Тл;
Тл; 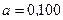 м.
м.
7. Рассчитаем работу
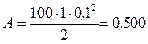 Дж.
Дж.
Ответ: 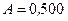 Дж.
Дж.
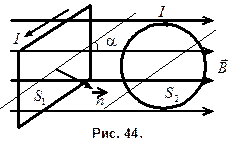 Пример 4. Квадратный контур со стороной
Пример 4. Квадратный контур со стороной 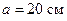 , в котором течет ток 8,0 А, находится в магнитном поле с индукцией 0,50 Тл. Плоскость контура образует с направлением линий индукции угол
, в котором течет ток 8,0 А, находится в магнитном поле с индукцией 0,50 Тл. Плоскость контура образует с направлением линий индукции угол 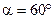 . Какую работу совершат силы Ампера, если при неизменной силе тока в контуре его форму изменить с квадрата на окружность (рис. 44)?
. Какую работу совершат силы Ампера, если при неизменной силе тока в контуре его форму изменить с квадрата на окружность (рис. 44)?
Решение.
1. Работа сил магнитного поля равна
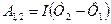 , (1)
, (1)
где 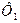 и
и 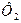 - магнитные потоки сквозь площадь квадрата и окружности. Магнитное поле в пределах контура однородно, а поверхность контура плоская, следовательно
- магнитные потоки сквозь площадь квадрата и окружности. Магнитное поле в пределах контура однородно, а поверхность контура плоская, следовательно
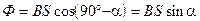 , (2)
, (2)
учитывая это
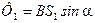 ; (3)
; (3)
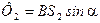 ; (4)
; (4)
 ; (5)
; (5)
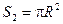 , (6)
, (6)
где R - радиус окружности.
2. Периметры контуров равны: 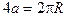 , откуда
, откуда
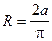 . (7)
. (7)
3. Подставляя (3)-(7) в (1), получаем расчетную формулу:
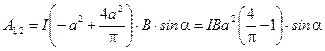 ;
;
4. Выполним расчеты
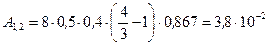 Дж.
Дж.
Ответ: 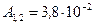 Дж.
Дж.
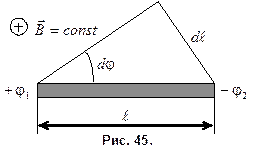 Пример 5. В однородном магнитном поле с индукцией
Пример 5. В однородном магнитном поле с индукцией 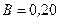 Тл вокруг оси, параллельной линиям индукции, вращается тонкий проводящий стержень длиной
Тл вокруг оси, параллельной линиям индукции, вращается тонкий проводящий стержень длиной 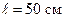 . Ось вращения перпендикулярна к стержню и проходит через один из его концов (рис. 45). Угловая скорость вращения стержня
. Ось вращения перпендикулярна к стержню и проходит через один из его концов (рис. 45). Угловая скорость вращения стержня 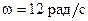 . Найти разность потенциалов между концами стержня.
. Найти разность потенциалов между концами стержня.
Решение. 1. Запишем уравнение электромагнитной индукции Фарадея:
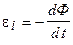 , (1)
, (1)
где dФ - элементарное изменение потока магнитной индукции, сцепленного со стержнем.
2. Разность потенциалов 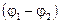 между концами стержня равна по модулю и противоположна по знаку ЭДС индукции
между концами стержня равна по модулю и противоположна по знаку ЭДС индукции 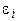 , возникающей в нем при вращении в магнитном поле:
, возникающей в нем при вращении в магнитном поле:
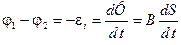 , (2)
, (2)
где B - индукция магнитного поля; dS - площадь, описываемая стержнем за время dt.
3. Найдем элементарную площадь формируемую стержнем при его вращении
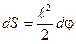 , (3)
, (3)
где  - угол поворота стержня за время dt.
- угол поворота стержня за время dt.
4. Подставляем (3) в (2) и, используя, что 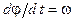 , получаем расчетную формулу
, получаем расчетную формулу
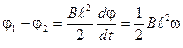 . (4)
. (4)
5. Выполним расчеты искомой величины
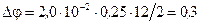 В.
В.
Ответ: 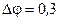 В.
В.
Пример 6. В однородном магнитном поле с индукцией 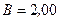 Тл движется протон. Траектория его движения представляет винтовую линию радиуса
Тл движется протон. Траектория его движения представляет винтовую линию радиуса 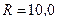 см с шагом
см с шагом 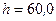 см. Заряд протона равен
см. Заряд протона равен 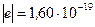 Кл, масса -
Кл, масса - 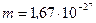 кг. Вычислить кинетическую энергию W протона.
кг. Вычислить кинетическую энергию W протона.
 Решение. 1. Составляющая скорости
Решение. 1. Составляющая скорости 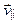 (см. рис. 46) не изменяется ни по модулю, ни по направлению. Составляющая скорости
(см. рис. 46) не изменяется ни по модулю, ни по направлению. Составляющая скорости 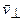 под действием силы Лоренца непрерывно меняет направление, оставаясь постоянной по модулю.
под действием силы Лоренца непрерывно меняет направление, оставаясь постоянной по модулю.
Таким образом, протон участвует в двух движениях: равномерном прямолинейном со скоростью 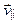 параллельно линиям индукции (вдоль оси OX) и по окружности со скоростью
параллельно линиям индукции (вдоль оси OX) и по окружности со скоростью 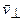 (постоянной по модулю) в плоскости YOZ.
(постоянной по модулю) в плоскости YOZ.
2. Кинетическая энергия протона:
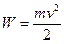 , (1)
, (1)
где
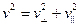 . (2)
. (2)
3. Шаг винтовой линии (смещение вдоль оси OX за время T одного оборота) равен
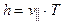 , (3)
, (3)
а период
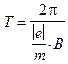 , (4)
, (4)
поэтому
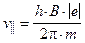 . (5)
. (5)
4. Второй закон Ньютона в случае криволинейного движения имеет вид
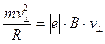 , (6)
, (6)
отсюда найдем перпендикулярную составляющую скорости
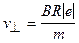 . (7)
. (7)
5. Подставляя выражения (5) и (7) в формулы (1) и (2), получим расчетную формулу для энергии
 или
или 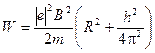 ;
;
 Дж.
Дж.
Ответ: 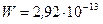 Дж.
Дж.
Пример 7. Соленоид содержит 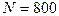 витков. Сечение сердечника из немагнитного материала имеет площадь
витков. Сечение сердечника из немагнитного материала имеет площадь 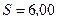 см2. Длина соленоида
см2. Длина соленоида 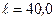 см. По обмотке соленоида протекает ток
см. По обмотке соленоида протекает ток 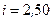 А. Найти среднее значение
А. Найти среднее значение 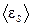 ЭДС самоиндукции, которая возникает в соленоиде, если ток уменьшается практически до нуля за время
ЭДС самоиндукции, которая возникает в соленоиде, если ток уменьшается практически до нуля за время 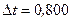 мс.
мс.
Решение.
1. Основной закон электромагнитной индукции:
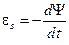 , (1)
, (1)
где Y - потокосцепление контура, определяемое по формуле
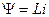 , (2)
, (2)
где L - индуктивность контура.
2. Объединяя (2) и (1), при 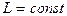 , получаем:
, получаем:
 . (3)
. (3)
3. Среднее значение ЭДС самоиндукции
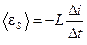 , (4)
, (4)
где  .
.
4. Индуктивность соленоида
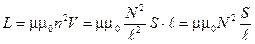 , (5)
, (5)
где n - число витков на единицу длины; магнитная проницаемость среды 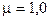 , магнитная постоянная
, магнитная постоянная  Н/А.
Н/А.
5. Объединив (1)-(4) получим расчетную формулу:
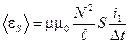 ; (6)
; (6)
6. Произведем расчеты
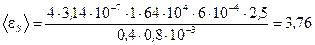 В.
В.
Ответ: 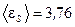 В.
В.
Пример 8. Найти энергию W магнитного поля катушки длиной 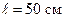 , состоящей из
, состоящей из 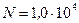 витков, вплотную прилегающих друг к другу (стержень изготовлен из немагнитного материала). Диаметр катушки
витков, вплотную прилегающих друг к другу (стержень изготовлен из немагнитного материала). Диаметр катушки 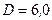 см, а сила тока
см, а сила тока 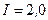 мА.
мА.
Решение.
1. Энергия магнитного поля соленоида с индуктивностью L, по обмотке которого течет ток силой I, выражается формулой
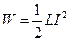 . (1)
. (1)
2. Индуктивность соленоида в случае немагнитного сердечника зависит только от числа витков на единицу длины и от объема сердечника
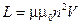 . (2)
. (2)
Учитывая, что 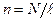 ,
,
 , (3)
, (3)
имеем
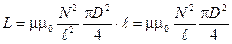 . (4)
. (4)
3. Подставляя (4) в (1), получаем расчетную формулу
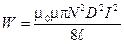 ;
;
4. Выполним расчеты
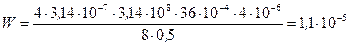 Дж.
Дж.
Ответ:  Дж
Дж
Контрольные задания
221.Ток силой 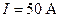 течет по проводнику, согнутому под прямым углом. Найти напряженность H магнитного поля в точке, лежащей на биссектрисе этого угла и отстоящей от вершины угла на расстоянии
течет по проводнику, согнутому под прямым углом. Найти напряженность H магнитного поля в точке, лежащей на биссектрисе этого угла и отстоящей от вершины угла на расстоянии 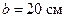 . Считать, что оба конца проводника находятся очень далеко от вершины угла.
. Считать, что оба конца проводника находятся очень далеко от вершины угла.
222.По проводнику, изогнутому в виде окружности, течет ток. Напряженность магнитного поля в центре окружности 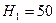 А/м. Не изменяя силы тока в проводнике, ему придали форму квадрата. Определить напряженность
А/м. Не изменяя силы тока в проводнике, ему придали форму квадрата. Определить напряженность  магнитного поля в точке пересечения диагоналей этого квадрата.
магнитного поля в точке пересечения диагоналей этого квадрата.
223.По контуру в виде равностороннего треугольника течет ток силой 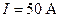 . Сторона треугольника
. Сторона треугольника 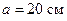 . Определить магнитную индукцию
. Определить магнитную индукцию 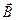 в точке пересечения высот.
в точке пересечения высот.
224.По проводнику, согнутому в виде прямоугольника со сторонами 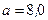 см и
см и 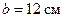 , течет ток силой
, течет ток силой 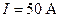 . Определить напряженность
. Определить напряженность 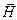 и индукцию
и индукцию 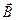 магнитного поля в точке пересечения диагоналей прямоугольника.
магнитного поля в точке пересечения диагоналей прямоугольника.
225.Ток 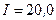 А, протекая по кольцу из медной проволоки сечением
А, протекая по кольцу из медной проволоки сечением 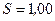 мм2, создает в центре кольца напряженность магнитного поля
мм2, создает в центре кольца напряженность магнитного поля 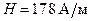 . Какая разность потенциалов U приложена к концам проволоки, образующей кольцо?
. Какая разность потенциалов U приложена к концам проволоки, образующей кольцо?
226.Найти напряженность 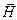 магнитного поля на оси кругового контура на расстоянии
магнитного поля на оси кругового контура на расстоянии 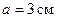 от его плоскости. Радиус контура
от его плоскости. Радиус контура 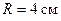 , ток в контуре
, ток в контуре 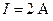 .
.
227.Напряженность магнитного поля в центре кругового витка 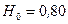 Э. Радиус витка
Э. Радиус витка 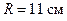 . Найти напряженность H магнитного поля на оси витка на расстоянии
. Найти напряженность H магнитного поля на оси витка на расстоянии 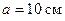 от его плоскости.
от его плоскости.
228.Два круговых витка радиусом 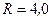 см каждый расположены в параллельных плоскостях на расстоянии
см каждый расположены в параллельных плоскостях на расстоянии 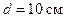 друг от друга. По виткам текут токи
друг от друга. По виткам текут токи 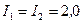 А. Найти напряженность H магнитного поля на оси витков в точке, находящейся на равном расстоянии от них. Задачу решить, когда: а) токи в витках текут в одном направлении; б) токи в витках текут в противоположных направлениях.
А. Найти напряженность H магнитного поля на оси витков в точке, находящейся на равном расстоянии от них. Задачу решить, когда: а) токи в витках текут в одном направлении; б) токи в витках текут в противоположных направлениях.
229.Два круговых витка радиусом 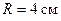 каждый расположены в параллельных плоскостях на расстоянии
каждый расположены в параллельных плоскостях на расстоянии 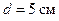 друг от друга. По виткам текут токи
друг от друга. По виткам текут токи 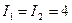 А. Найти напряженность H магнитного поля в центре одного из витков. Задачу решить, когда: а) токи в витках текут в одном направлении; б) токи в витках текут в противоположных направлениях.
А. Найти напряженность H магнитного поля в центре одного из витков. Задачу решить, когда: а) токи в витках текут в одном направлении; б) токи в витках текут в противоположных направлениях.
230.Два круговых витка расположены в двух взаимно перпендикулярных плоскостях так, что центры этих витков совпадают. Радиус каждого витка 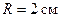 , токи в витках
, токи в витках  А. Найти напряженность H магнитного поля в центре этих витков.
А. Найти напряженность H магнитного поля в центре этих витков.
231.По двум параллельным проводам длиной 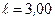 мм каждый текут одинаковые токи силой
мм каждый текут одинаковые токи силой 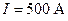 . Расстояние между проводниками
. Расстояние между проводниками 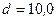 см. Определить силу
см. Определить силу 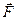 взаимодействия проводников.
взаимодействия проводников.
232.По трем параллельным прямым проводам, находящимся на одинаковом расстоянии 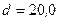 см друг от друга, текут токи одинаковой силы
см друг от друга, текут токи одинаковой силы 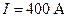 . В двух проводах направления токов совпадают. Вычислить силу F, действующую на единицу длины каждого провода.
. В двух проводах направления токов совпадают. Вычислить силу F, действующую на единицу длины каждого провода.
233.Квадратная проволочная рама расположена в одной плоскости с длинным прямым проводом так, что две ее стороны параллельны проводу. По рамке и проводу текут одинаковые токи силой 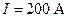 . Определить силу F, действующую на рамку, если ближайшая к проводу сторона рамки находится от него на расстоянии, равном ее длине.
. Определить силу F, действующую на рамку, если ближайшая к проводу сторона рамки находится от него на расстоянии, равном ее длине.
234.Прямой провод длиной 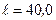 см, по которому течет ток силой
см, по которому течет ток силой 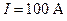 , движется в однородном магнитном поле с индукцией
, движется в однородном магнитном поле с индукцией 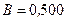 Тл. Какую работу A совершат силы, действующие на провод со стороны поля, переместив его на расстояние
Тл. Какую работу A совершат силы, действующие на провод со стороны поля, переместив его на расстояние 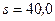 см, если направление перемещения перпендикулярно линиям индукции и проводу?
см, если направление перемещения перпендикулярно линиям индукции и проводу?
235.Напряженность H магнитного поля в центре кругового витка равна 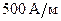 . Магнитный момент витка
. Магнитный момент витка 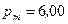 А·м2. Вычислить силу тока I в витке и радиус R витка.
А·м2. Вычислить силу тока I в витке и радиус R витка.
236.Короткая катушка площадью поперечного сечения 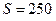 см2, содержащая
см2, содержащая 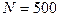 витков провода, по которому течет ток силой
витков провода, по которому течет ток силой 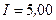 А, помещена в однородное магнитное поле напряженностью
А, помещена в однородное магнитное поле напряженностью 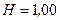 кА/м. Найти: 1) магнитный момент
кА/м. Найти: 1) магнитный момент 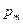 катушки; 2) вращающий момент M, действующий на катушку, если ось катушки составляет угол
катушки; 2) вращающий момент M, действующий на катушку, если ось катушки составляет угол 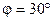 с линиями поля.
с линиями поля.
237.Виток диаметром 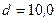 см должен вращаться около вертикальной оси, совпадающей с одним из диаметров витка. Виток установили в плоскости магнитного меридиана и пустили по нему ток силой
см должен вращаться около вертикальной оси, совпадающей с одним из диаметров витка. Виток установили в плоскости магнитного меридиана и пустили по нему ток силой 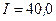 А. Какой вращающий момент M нужно приложить к витку, чтобы удержать его в начальном положении? Горизонтальную составляющую индукции магнитного поля Земли принять равной
А. Какой вращающий момент M нужно приложить к витку, чтобы удержать его в начальном положении? Горизонтальную составляющую индукции магнитного поля Земли принять равной 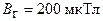 .
.
238.Виток радиусом 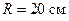 , по которому течет ток силой
, по которому течет ток силой 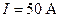 , свободно установился в однородном магнитном поле напряженностью
, свободно установился в однородном магнитном поле напряженностью 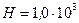 А/м. Виток повернули относительно диаметра на угол
А/м. Виток повернули относительно диаметра на угол 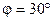 . Определить совершенную работу A.
. Определить совершенную работу A.
239.На оси контура с током, магнитный момент которого 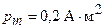 , находится другой такой же контур. Магнитный момент второго контура перпендикулярен оси. Вычислить механический момент M, действующий на второй контур. Расстояние между контурами
, находится другой такой же контур. Магнитный момент второго контура перпендикулярен оси. Вычислить механический момент M, действующий на второй контур. Расстояние между контурами 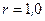 м. Размеры контуров малы по сравнению с расстоянием между ними.
м. Размеры контуров малы по сравнению с расстоянием между ними.
240.По витку радиусом 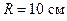 течет ток силой
течет ток силой 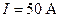 . Виток помещен в однородное магнитное поле индукцией
. Виток помещен в однородное магнитное поле индукцией 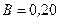 Тл. Определить момент силы M, действующей на виток, если плоскость витка составляет угол
Тл. Определить момент силы M, действующей на виток, если плоскость витка составляет угол 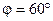 с линиями индукции.
с линиями индукции.
241.Электрон движется по окружности в однородном магнитном поле с напряженностью 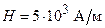 . Определить частоту обращения n электрона.
. Определить частоту обращения n электрона.
242.Электрон движется в магнитном поле с индукцией 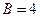 Тл по окружности радиусом
Тл по окружности радиусом  . Какова кинетическая энергия T электрона?
. Какова кинетическая энергия T электрона?
243.Протон влетел в однородное магнитное поле под углом 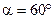 к направлению линий поля и движется по спирали, радиус которой
к направлению линий поля и движется по спирали, радиус которой 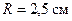 . Индукция магнитного поля
. Индукция магнитного поля 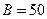 мТл. Найти кинетическую энергию T протона.
мТл. Найти кинетическую энергию T протона.
244.Протон и a-частица, ускоренные одинаковой разностью потенциалов, влетают в однородное магнитное поле. Во сколько раз радиус 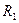 кривизны траектории протона больше радиуса
кривизны траектории протона больше радиуса  кривизны траектории a-частицы?
кривизны траектории a-частицы?
245.Два иона с одинаковыми зарядами, пройдя одну и ту же ускоряющую разность потенциалов, влетели в однородное магнитное поле перпендикулярно линиям индукции. Один ион, масса которого  а.е.м. (атомная единица массы), описал дугу окружности радиусом
а.е.м. (атомная единица массы), описал дугу окружности радиусом 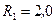 см. Определить массу
см. Определить массу 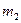 (в а.е.м.) другого иона, который описал дугу окружности радиусом
(в а.е.м.) другого иона, который описал дугу окружности радиусом 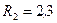 см.
см.
246.Протон движется по окружности в однородном магнитном поле с индукцией 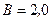 Тл. Определить силу I эквивалентного кругового тока, создаваемого движением протона.
Тл. Определить силу I эквивалентного кругового тока, создаваемого движением протона.
247.Электрон движется в однородном магнитном поле с индукцией 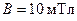 по винтовой линии, радиус которой
по винтовой линии, радиус которой 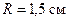 и шаг
и шаг 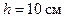 . Определить период T обращения электрона и его скорость v.
. Определить период T обращения электрона и его скорость v.
248.В однородном магнитном поле с индукцией 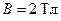 движется a-частица. Траектория ее движения представляет собой винтовую линию радиусом
движется a-частица. Траектория ее движения представляет собой винтовую линию радиусом 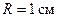 и шагом
и шагом 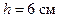 . Определить кинетическую энергию T протона.
. Определить кинетическую энергию T протона.
249.Перпендикулярно магнитному полю напряженностью 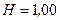 кА/м возбуждено электрическое поле напряженностью
кА/м возбуждено электрическое поле напряженностью 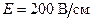 . Перпендикулярно обоим полям движется, не отклоняясь от прямолинейной траектории, заряженная частица. Определить скорость v частицы.
. Перпендикулярно обоим полям движется, не отклоняясь от прямолинейной траектории, заряженная частица. Определить скорость v частицы.
250.Заряженная частица прошла ускоряющую разность потенциалов и влетела в скрещенные под прямым углом электрическое ( 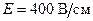 ) и магнитное (
) и магнитное ( 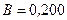 Тл) поля. Определить ускоряющую разность потенциалов U, если, двигаясь перпендикулярно обоим полям, частица не испытывает отклонений от прямолинейной траектории. Отношение заряда к массе частицы
Тл) поля. Определить ускоряющую разность потенциалов U, если, двигаясь перпендикулярно обоим полям, частица не испытывает отклонений от прямолинейной траектории. Отношение заряда к массе частицы 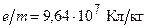 .
.
251.Плоский контур площадью  см2 находится в однородном магнитном поле с индукцией
см2 находится в однородном магнитном поле с индукцией  мТл. Определить магнитный поток
мТл. Определить магнитный поток 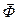 , пронизывающий контур, если плоскость его составляет угол
, пронизывающий контур, если плоскость его составляет угол 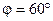 с направлением линий индукции.
с направлением линий индукции.
252.Магнитный поток Ф через сечение соленоида равен 50 мкВб. Длина соленоида 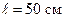 . Найти магнитный момент
. Найти магнитный момент 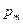 соленоида, если его витки плотно прилегают друг к другу.
соленоида, если его витки плотно прилегают друг к другу.
253.В средней части соленоида, содержащего 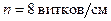 , помещен круговой виток диаметром
, помещен круговой виток диаметром  . Плоскость витка расположена под углом
. Плоскость витка расположена под углом 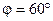 к оси соленоида. Определить магнитный поток Ф, пронизывающий виток, если по обмотке соленоида течет ток силой
к оси соленоида. Определить магнитный поток Ф, пронизывающий виток, если по обмотке соленоида течет ток силой 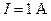 .
.
254.На длинный картонный каркас диаметром 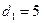 см уложена однослойная обмотка (виток к витку) из проволоки диаметром
см уложена однослойная обмотка (виток к витку) из проволоки диаметром 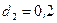 см. Определить магнитный поток Ф, создаваемый таким соленоидом при силе тока
см. Определить магнитный поток Ф, создаваемый таким соленоидом при силе тока  .
.
255.Квадратный контур со стороной 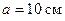 , в котором течет ток силой
, в котором течет ток силой  А, находится в магнитном поле с индукцией
А, находится в магнитном поле с индукцией 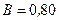 Тл под углом
Тл под углом  к линиям индукции. Какую работу A нужно совершить, чтобы при неизменной силе тока в контуре изменить его форму с квадрата на окружность?
к линиям индукции. Какую работу A нужно совершить, чтобы при неизменной силе тока в контуре изменить его форму с квадрата на окружность?
256.Плоский контур с током силой 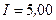 А свободно установился в однородном магнитном поле с индукцией
А свободно установился в однородном магнитном поле с индукцией  Тл. Площадь контура
Тл. Площадь контура 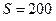 см2. Поддерживая ток в контуре неизменным, его повернули относительно оси, лежащей в плоскости контура, на угол
см2. Поддерживая ток в контуре неизменным, его повернули относительно оси, лежащей в плоскости контура, на угол 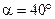 . Определить совершенную при этом работу A.
. Определить совершенную при этом работу A.
257.Виток, в котором поддерживается постоянная сила тока 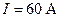 , свободно установился в однородном магнитном поле (
, свободно установился в однородном магнитном поле ( 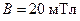 ). Диаметр витка
). Диаметр витка 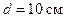 . Какую работу A нужно совершить для того, чтобы повернуть виток относительно оси, совпадающей с диаметром, на угол
. Какую работу A нужно совершить для того, чтобы повернуть виток относительно оси, совпадающей с диаметром, на угол 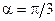 ?
?
258.В однородном магнитном поле перпендикулярно линиям индукции расположен плоский контур площадью 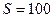 см2. Поддерживая в контуре постоянную силу тока
см2. Поддерживая в контуре постоянную силу тока 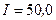 А, его переместили из поля в область пространства, где поле отсутствует. Определить индукцию B магнитного поля, если при перемещении контура была совершена работа
А, его переместили из поля в область пространства, где поле отсутствует. Определить индукцию B магнитного поля, если при перемещении контура была совершена работа  Дж.
Дж.
259.В однородном магнитном поле напряженностью 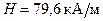 помещена квадратная рамка, плоскость которой составляет с направлением магнитного поля угол
помещена квадратная рамка, плоскость которой составляет с направлением магнитного поля угол 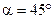 . Сторона рамки
. Сторона рамки 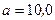 см. Найти магнитный поток Ф, пронизывающий рамку.
см. Найти магнитный поток Ф, пронизывающий рамку.
260.В магнитном поле, индукция которого 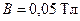 , вращается стержень длиной
, вращается стержень длиной 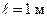 . Ось вращения, проходящая через один из концов стержня, параллельна направлению магнитного поля. Найти магнитный поток Ф, пересекаемый стержнем при каждом обороте.
. Ось вращения, проходящая через один из концов стержня, параллельна направлению магнитного поля. Найти магнитный поток Ф, пересекаемый стержнем при каждом обороте.
261.Проводник длиной 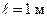 движется со скоростью
движется со скоростью 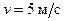 перпендикулярно линиям индукции однородного магнитного поля. Определить магнитную индукцию B, если на концах проводника возникает разность потенциалов
перпендикулярно линиям индукции однородного магнитного поля. Определить магнитную индукцию B, если на концах проводника возникает разность потенциалов 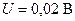 .
.
262.Рамка площадью 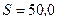 см2, содержащая
см2, содержащая 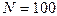 витков, равномерно вращается в однородном магнитном поле (
витков, равномерно вращается в однородном магнитном поле ( 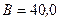 мТл). Определить максимальную ЭДС индукции
мТл). Определить максимальную ЭДС индукции 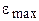 , если ось вращения лежит в плоскости рамки и перпендикулярна линиям индукции, а рамка вращается с частотой
, если ось вращения лежит в плоскости рамки и перпендикулярна линиям индукции, а рамка вращается с частотой 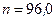 об/мин.
об/мин.
263.Кольцо из проволоки сопротивлением 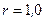 МОм находится в однородном магнитном поле (
МОм находится в однородном магнитном поле ( 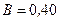 Тл). Плоскость кольца составляет угол
Тл). Плоскость кольца составляет угол 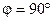 с линиями индукции. Определить заряд Q, который протечет по кольцу, если его выдернуть из поля. Площадь кольца
с линиями индукции. Определить заряд Q, который протечет по кольцу, если его выдернуть из поля. Площадь кольца 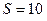 см2.
см2.
264.В магнитном поле, индукция которого 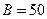 мТл, вращается стержень длиной
мТл, вращается стержень длиной 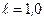 м с угловой скоростью
м с угловой скоростью 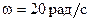 . Ось вращения проходит через конец стержня и параллельна магнитному полю. Найти ЭДС индукции e, возникающую на концах стержня.
. Ось вращения проходит через конец стержня и параллельна магнитному полю. Найти ЭДС индукции e, возникающую на концах стержня.
265.Катушка диаметром 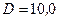 см, состоящая из
см, состоящая из 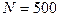 витков проволоки, находится в магнитном поле. Найти среднюю ЭДС индукции
витков проволоки, находится в магнитном поле. Найти среднюю ЭДС индукции 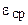 , возникающую в этой катушке, если индукция магнитного поля B увеличивается в течение времени
, возникающую в этой катушке, если индукция магнитного поля B увеличивается в течение времени 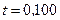 с от 0,00 до 2,00 Тл.
с от 0,00 до 2,00 Тл.
266.На соленоид длиной  м и площадью поперечного сечения
м и площадью поперечного сечения 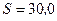 см2 надет проволочный виток. Обмотка соленоида имеет
см2 надет проволочный виток. Обмотка соленоида имеет 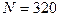 витков и по нему идет ток
витков и по нему идет ток 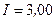 А. Какая средняя ЭДС
А. Какая средняя ЭДС 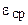 индуцируется в надетом на соленоид витке, когда ток в соленоиде выключается в течение времени
индуцируется в надетом на соленоид витке, когда ток в соленоиде выключается в течение времени 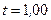 мс?
мс?
267.Какая средняя ЭДС 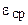 индуцируется в витке, если соленоид, рассмотренный в предыдущей задаче, имеет железный сердечник?
индуцируется в витке, если соленоид, рассмотренный в предыдущей задаче, имеет железный сердечник?
268.На соленоид длиной 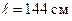 и диаметром
и диаметром 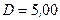 см надет проволочный виток. Обмотка соленоида имеет
см надет проволочный виток. Обмотка соленоида имеет 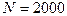 витков, и по ней течет ток
витков, и по ней течет ток 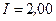 А. Соленоид имеет железный сердечник. Какая средняя ЭДС
А. Соленоид имеет железный сердечник. Какая средняя ЭДС 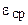 индуцируется в надетом на соленоид витке, когда ток в соленоиде выключается в течение времени
индуцируется в надетом на соленоид витке, когда ток в соленоиде выключается в течение времени 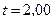 мс?
мс?
269.В однородном магнитном поле, индукция которого 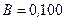 Тл, вращается катушка, состоящая из
Тл, вращается катушка, состоящая из 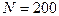 витков. Ось вращения катушки перпендикулярна к ее оси и к направлению магнитного поля. Период обращения катушки
витков. Ось вращения катушки перпендикулярна к ее оси и к направлению магнитного поля. Период обращения катушки 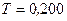 с; площадь поперечного сечения
с; площадь поперечного сечения 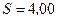 см2. Найти максимальную ЭДС индукции
см2. Найти максимальную ЭДС индукции 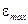 во вращающейся катушке.
во вращающейся катушке.
270.Рамка, содержащая  витков площадью
витков площадью 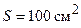 , равномерно вращается с частотой
, равномерно вращается с частотой 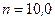 с-1 в магнитном поле напряженностью
с-1 в магнитном поле напряженностью 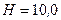 кА/м. Ось вращения лежит в плоскости рамки и перпендикулярна линиям напряженности. Определить максимальную ЭДС индукции
кА/м. Ось вращения лежит в плоскости рамки и перпендикулярна линиям напряженности. Определить максимальную ЭДС индукции 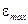 , возникающую в рамке.
, возникающую в рамке.
271.Соленоид содержит 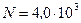 витков провода, по которому течет ток силой
витков провода, по которому течет ток силой 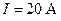 . Определить магнитный поток Ф и потокосцепление Y, если индуктивность
. Определить магнитный поток Ф и потокосцепление Y, если индуктивность 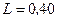 Гн.
Гн.
272.На картонный каркас длиной 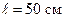 и площадью сечения
и площадью сечения 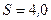 см2 намотан в один слой провод диаметром
см2 намотан в один слой провод диаметром 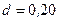 мм так, что витки плотно прилегают друг к другу (тол-щиной изоляции пренебречь). Определить индуктивность L получившегося соленоида.
мм так, что витки плотно прилегают друг к другу (тол-щиной изоляции пренебречь). Определить индуктивность L получившегося соленоида.
273.Определить силу тока в цепи через  с после ее размыкания. Сопротивление цепи
с после ее размыкания. Сопротивление цепи 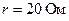 и индуктивность
и индуктивность 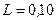 Гн. Сила тока до размыкания цепи
Гн. Сила тока до размыкания цепи 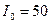 А.
А.
274.По обмотке соленоида индуктивностью  Гн течет ток силой
Гн течет ток силой  . Определить энергию W магнитного поля соленоида.
. Определить энергию W магнитного поля соленоида.
275.В электрической цепи, содержащей сопротивление 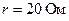 и индуктивность
и индуктивность 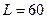 мГн, течет ток силой
мГн, течет ток силой 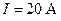 . Определить силу тока в цепи через
. Определить силу тока в цепи через 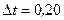 мс после ее размыкания.
мс после ее размыкания.
276.По замкнутой цепи с сопротивлением 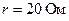 течет ток. По истечении времени
течет ток. По истечении времени 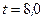 мс после размыкания цепи сила тока в ней уменьшилась в 20 раз. Определить индуктивность цепи.
мс после размыкания цепи сила тока в ней уменьшилась в 20 раз. Определить индуктивность цепи.
277.По проводнику, изогнутому в виде кольца радиусом 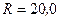 см, содержащему
см, содержащему 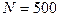 витков, течет ток силой
витков, течет ток силой 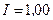 А. Определить объемную плотность w энергии магнитного поля в центре кольца.
А. Определить объемную плотность w энергии магнитного поля в центре кольца.
278.При какой силе тока I в прямолинейном проводе бесконечной длины на расстоянии 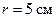 от него объемная плотность энергии магнитного поля будет
от него объемная плотность энергии магнитного поля будет 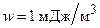 ?
?
279.Обмотка тороида имеет 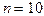 витков на каждый сантиметр длины (по средней линии тороида). Вычислить объемную плотность энергии w магнитного поля при силе тока
витков на каждый сантиметр длины (по средней линии тороида). Вычислить объемную плотность энергии w магнитного поля при силе тока  . Сердечник выполнен из немагнитного материала и магнитное поле во всем объеме однородно.
. Сердечник выполнен из немагнитного материала и магнитное поле во всем объеме однородно.
280.Обмотка соленоида содержит 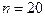 витков на каждый сантиметр длины. При какой силе тока I объемная плотность энергии магнитного поля будет
витков на каждый сантиметр длины. При какой силе тока I объемная плотность энергии магнитного поля будет 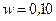 Дж/м3? Сердечник выполнен из немагнитного материала, и магнитное поле в всем объеме однородно.
Дж/м3? Сердечник выполнен из немагнитного материала, и магнитное поле в всем объеме однородно.
| <== предыдущая страница | | | следующая страница ==> |
| Решение. 1.Находим высоту монтажного горизонта | | | РАЗДЕЛ 4. СТРАТИГРАФИЯ И ПЛАТФОРМЕННЫЙ МАГМАТИЗМ ВЕРХНЕГО ПРОТЕРОЗОЯ |
Дата добавления: 2014-10-10; просмотров: 1890; Нарушение авторских прав

Мы поможем в написании ваших работ!