Взаимосвязь направляющих углов вектора Пойнтинга на границе раздела диэлектрических сред

Пусть однородная плоская (парциальная) волна падает на плоскую поверхность раздела изотропных однородных диэлектриков, диэлектрические и магнитные проницаемости которых соответственно равны и 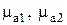. Падающая волна на границе раздела в общем случае частично отражается в первую среду, частично проходит во вторую. Углы, образуемые положительными направлениями осей координат 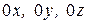с векторами Пойнтинга падающей, отраженной и прошедшей волн обозначаем соответственно: 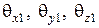; ; 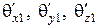. Выражения для векторных комплексных амплитуд напряженностей электрического и магнитного поля падающей, отраженной и прошедшей волн будут иметь вид:

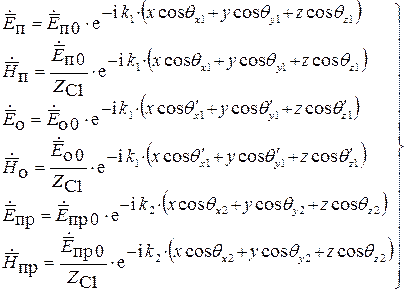, (6.44)

где 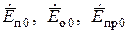– комплексные векторные амплитуды напряженности электрического поля падающей, отраженной и прошедшей волн на границе раздела при условии, что 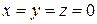соответственно,

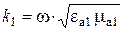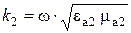, – фазовые постоянные,

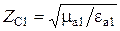, – характеристические сопротивления волн в первой и второй средах без потерь соответственно.

Для определения соотношений, связывающих пространственные углы, воспользуемся любым из граничных условий, например, условием непрерывности касательной составляющей вектора 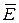полного поля на поверхности раздела .

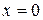При этом с учетом (6.44) получаем

. (6.45)

Равенство (6.45) должно выполняться при любых значениях 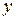и 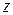, в том числе, и при условии 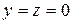, когда

. (6.46)

Учитывая (6.45) и (6.46), записываем условия их выполнения:

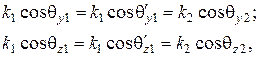(6.47)

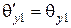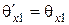откуда следует, что , и, следовательно, , а также

. (6.48)

Поскольку сумма квадратов направляющих косинусов любого радиус-вектора равна единице, поэтому

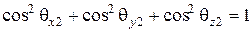, (6.49)

и с учетом (6.48)

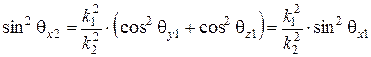, (6.50)

то есть

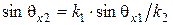. (6.51)

Угол 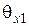, образуемый вектором Пойнтинга падающей волны и нормалью к поверхности раздела сред (осью 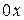) называется углом падения. Угол между этой же нормалью и направлением распространения отраженной волны – угол отражения и, наконец, угол 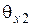между вектором Пойнтинга прошедшей волны и нормалью называется углом преломления. Таким образом, соотношение между углом падения волны и углом преломления подчиняется закону синусов (закон Снеллиуса) (выражение 6.51), а соотношения между парой других углов, характеризующих направления распространения падающей и преломленной волн, подчиняются закону косинусов (6.48).

Косинус угла преломления можно определить из (6.51)

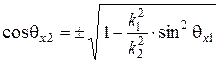. (6.52)

Полное внутреннее отражение волны возможно при неравенстве , как это следует из (6.51). При критическом угле падения 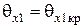угол преломления равен , то есть , поэтому в соответствии с (6.51), имеем

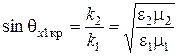, (6.53)

где 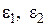– относительные диэлектрические проницаемости,

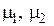– относительные магнитные проницаемости.

При 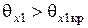, то есть при наличии полного внутреннего отражения, что имеет место при волноводном распространении волны, угол преломления становится комплексным, а косинус этого угла – мнимой величиной

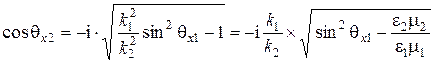. (6.54)

Как видно из выражения (6.48) косинусы других углов: 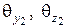остаются вещественными.

При подстановке (6.48) и (6.54) в (6.44) для комплексной амплитуды преломленной волны получаем выражение

, (6.55)

где .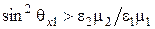

Из (6.55) следует, что напряженность поля в направлении оси 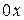, то есть в направлении, перпендикулярном плоскости раздела, во второй среде экспоненциально убывает; волновой характер поля в этом направлении отсутствует. В других направлениях вне волновода, волновой характер поля сохраняется. Если бы в выражении (6.54) перед квадратным корнем был выбран знак “+”, то при увеличении расстояния 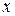от плоскости раздела во второй среде амплитуда поля неограниченно бы возрастала, что лишено физического смысла.

Дата добавления: 2014-10-10; просмотров: 545; Нарушение авторских прав

Мы поможем в написании ваших работ!