Преобразование поляризации парциальных волн в диэлектрическом волноводе

Рассмотрим падение плоской линейно поляризованной волны на стенки волновода ( и 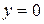), ограниченного со всех сторон диэлектрической средой с относительной диэлектрической проницаемостью, равной 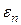. Относительную диэлектрическую проницаемость материала волновода обозначим . Векторы Пойнтинга парциальных волн, проекции которых на плоскость 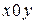изображены на рисунке 6.3, характеризуются следующими направляющими углами:

; ;

; .

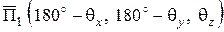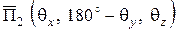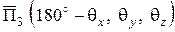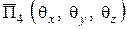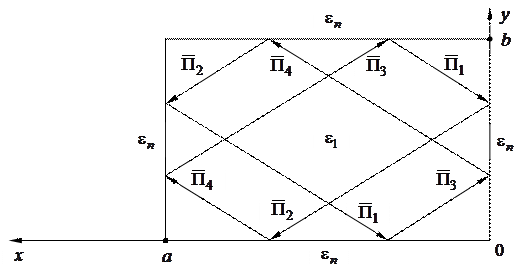Рисунок 6.3 – Схематическое изображение поперечного сечения волновода и

проекций векторов Пойнтинга парциальных волн на поперечную плоскость

Пусть на границу раздела сред 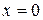падает плоская нормально поляризованная волна

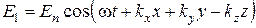. (6.56)

Вектор напряженности электрического поля 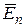этой волны перпендикулярен плоскости, проходящей через направление распространения 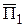волны и ось 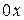, и имеет две проекции: на ось 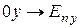и на ось 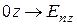; проекция на ось 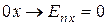. При выполнении условия полного внутреннего отражения напряженность 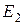электрического поля отраженной волны в направлении определяется выражением

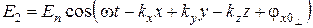, (6.57)

где , , , ,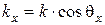

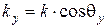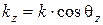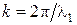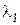– длина волны в диэлектрике с относительной диэлектрической проницаемостью, равной ,

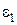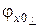– фаза коэффициента отражения нормально поляризованной волны, равная

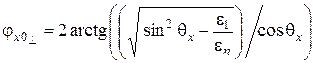. (6.58)

Рассматриваемая волна 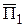падает также и на границу раздела сред 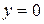, для которой плоскость падения проходит через вектор 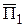и ось 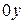. Относительно этой плоскости падения вектор 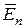имеет две составляющие: лежащую в плоскости и перпендикулярную к ней. При выполнении условия полного внутреннего отражения параллельно поляризованная составляющая волны и перпендикулярно поляризованная будут отличаться не только по амплитуде 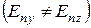, но и по фазе. Фаза коэффициента отражения параллельно поляризованной волны описывается выражением

, (6.59)

а фаза коэффициента отражения нормально поляризованной волны

. (6.60)

Вследствие этого суммарная отраженная волна в направлении 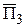будет иметь эллиптическую поляризацию. Проведенный анализ показывает, что амплитуды напряженностей электрического поля равны:

· параллельно поляризованной волны –

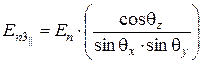; (6.61)

· нормально поляризованной –

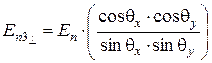. (6.62)

Таким образом, после отражения линейно поляризованной волны 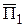от границы раздела сред 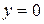на грань 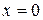будут падать уже две линейно поляризованные волны, у которых:

; (6.63)

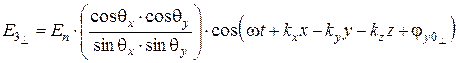. (6.64)

Каждая из этих волн состоит из двух составляющих, одна из них перпендикулярно поляризована к плоскости падения на грань 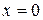, другая 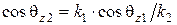параллельно. Отраженная от этой границы суммарная волна в направлении 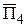будет состоять из четырех линейно поляризованных волн, напряженности электрического поля которых определяются выражениями:

; (6.65)

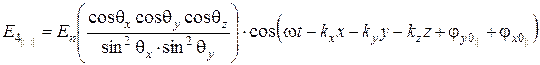; (6.66)

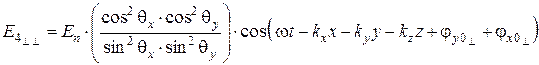; (6.67)

; (6.68)

где 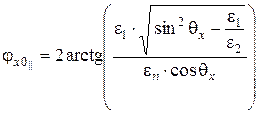. (6.69)

Суммарная волна, отраженная от грани 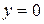в направлении 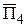, также состоит из четырех линейно поляризованных волн, выражения для напряженностей электрического поля которых имеют вид:

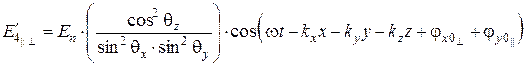; (6.70)

; (6.71)

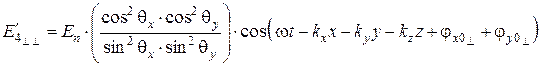; (6.72)

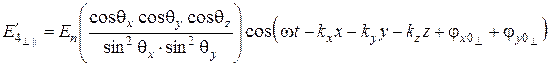, (6.73)

Из сопоставления (6.65) и (6.70), (6.66) и (6.71), (6.67) и (6.72), (6.68) и (6.73) видно, что

, , , .

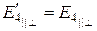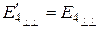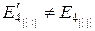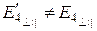Таким образом, при падении линейно поляризованной волны на границы раздела 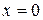и 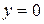, причем для границы 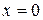она является нормально поляризованной, возникает одиннадцать отраженных линейно поляризованных волн. Шесть из них, включая падающую, являются нормально поляризованными относительно грани 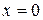, другие шесть – параллельно поляризованными. Напряженности электрических полей этих волн определяются выражениями:

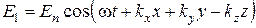; (6.74)

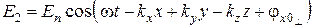; (6.75)

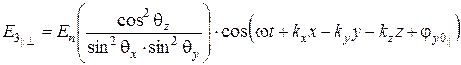; (6.76)

; (6.77)

; (6.78)

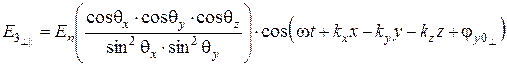; (6.79)

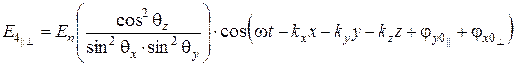; (6.80)

; (6.81)

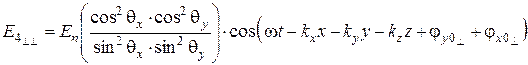; (6.82)

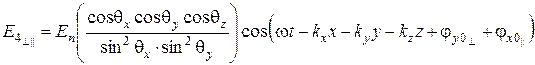; (6.83)

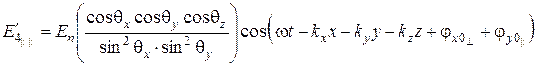; (6.84)

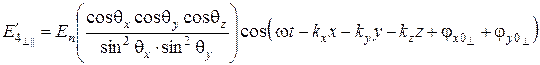. (6.85)

Дата добавления: 2014-10-10; просмотров: 349; Нарушение авторских прав

Мы поможем в написании ваших работ!