Интерпретация собственных полей прямоугольного волновода и его модификаций

В волноводах прямоугольного сечения: полых металлических, металлодиэлектрических, диэлектрических распространение плоской волны вдоль оси волновода невозможно. Это связано с двумя обстоятельствами: во-первых, с замкнутостью магнитных силовых линий и, во-вторых, эти линии должны охватывать либо ток проводимости, либо ток смещения.

Допустим, плоская волна распространяется в волноводе вдоль оси 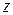(рисунок 6.1).

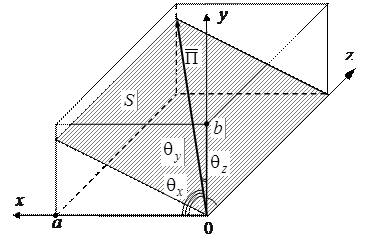Рисунок 6.1 – Прямоугольный волновод и система координат

В этом случае векторы напряженностей электрического и магнитного полей должны лежать в поперечной плоскости, например, . Но вследствие замкнутости линий магнитного поля должна существовать еще его продольная составляющая . В результате этого вектор направления распространения плоской волны составит с осью угол 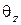. Если же линия магнитного поля лежит в поперечной плоскости, то она должна охватывать ток смещения. Следовательно, вектор 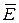будет иметь продольную составляющую. И опять плоская волна обязана распространяться под углом к оси волновода.

В общем случае вектор Пойнтинга плоской волны, распространяющейся в волноводе, образует с осями координат 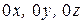углы, соответственно равные: (см. рисунок 6.1). Направляющие косинусы этих углов связаны между собой известным соотношением

. (6.1)

Структуру электромагнитного поля в волноводах можно рассматривать как результат сложения плоских однородных волн, называемых парциальными, многократно отраженных от его граничных поверхностей, то есть, допустима лучевая трактовка явлений в волноводах [12]. Такой подход обеспечивает физическую наглядность и простоту понимания пространственной картины поля на всех этапах решения задачи, приводя к конечным выражениям для составляющих векторов поля, полностью совпадающим с решением уравнений Максвелла.

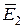Как показано в первой части пособия, любая однородная плоская волна линейной, круговой или эллиптической поляризации может быть представлена суммой двух линейно поляризованных плоских волн, имеющих взаимно перпендикулярные векторы и (и , ). Разложение на две ортогональные линейно поляризованные волны может быть произведено по двум произвольным взаимно перпендикулярным ортам, лежащим в поперечной по отношению к направлению распространения плоскости и называемым поляризационным базисом.

Векторы 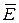и плоской волны перпендикулярны направлению распространения 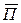(рисунок 6.1), вследствие векторного соотношения 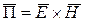, кроме того, они взаимно перпендикулярны. Разложим вектор 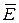на две ортогональные составляющие и 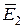. Для упрощения математической записи проекций векторов поля на оси координат плоскость поляризационного базиса ориентируем перпендикулярно плоскости , проходящей через вектор и одну из координатных осей. 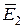Один из векторов, например , пусть будет перпендикулярен плоскости , тогда другой вектор – будет лежать в этой плоскости. Волну, вектор которой перпендикулярен плоскости , будем называть нормально поляризованной. Другую волну с вектором 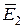назовем параллельно поляризованной.

Возможны три варианта расположения упомянутой плоскости :

1. Плоскость проходит через вектор и ось (рисунок 6.1). Вектор , перпендикулярный плоскости, будет иметь две составляющие и , проекция вектора на ось будет равна нулю, то есть . Вектор перпендикулярен вектору и лежит в плоскости . Он имеет три проекции , , . У параллельно поляризованной волны вектор 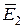лежит в плоскости . Он имеет все три проекции на координатные оси 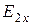, , 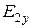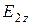. 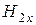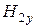Вектор этой волны перпендикулярен плоскости, поэтому имеет только две проекции и , а 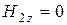. Сравнивая собственные поля 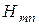и 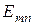в металлическом прямоугольном волноводе с ортогональными линейно поляризованными плоскими волнами, видим, что одна из них – нормально поляризованная имеет те же проекции векторов, как и 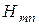, другая – параллельно поляризованная волна соответствует .

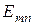Таким образом, для анализа электромагнитного поля в прямоугольном металлическом волноводе выбирается первый вариант расположения плоскости , проходящей через вектор и ось .

2. Плоскость проходит через вектор и ось 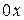. Этот вариант расположения плоскости изображен на рисунке 6.2.

Рисунок 6.2 – Плоскость проходит через вектор и ось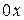

Вектор нормально поляризованной волны в этом случае имеет составляющие , , , а : , , 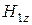. Вектор 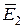параллелен плоскости , поэтому имеет все три проекции: 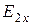, , 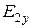, 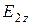а вектор перпендикулярен плоскости и оси 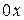имеет только две проекции 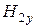, , при этом .

Данный вариант ориентации поляризационного базиса используется при анализе диэлектрического и металлодиэлектрических волноводов прямоугольного сечения. Нормально поляризованная волна соответствует собственному полю , а параллельно поляризованная - .

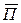3. Плоскость проходит через вектор и ось 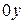. Векторы и нормально поляризованной волны имеют составляющие , , , , , , 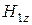а векторы 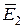и параллельно поляризованной волны - , , , , , .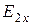

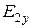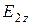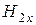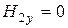Результирующая плоская волна с векторам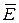и и в общем случае имеет все шесть составляющих:

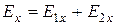; (6.2)

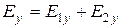; (6.3)

; (6.4)

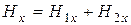; (6.5)

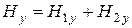; (6.6)

. (6.7)

Все варианты поляризационных базисов равноценны. В этом можно убедиться, если сравнить составляющие векторов 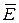и , найденные в результате анализа поля в прямоугольном металлическом волноводе по всем трем вариантам.

Как показано ниже, любая составляющая векторов 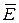и может быть представлена выражением

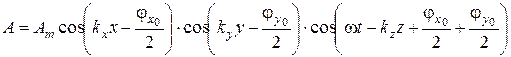, (6.8)

где 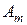– амплитуда составляющей, независимая от пространственных координат и времени; , , – проекции волнового вектора 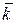на оси координат; 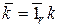– волновой вектор, равный по величине коэффициенту распространения волны в данной среде 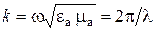, и совпадающий по направлению с вектором Пойнтинга ; 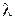– длина волны в среде с параметрами 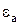, ; , – фазы коэффициентов отражения составляющих векторов поля от границы и соответственно.

Для металлического волновода и могут принимать значения, равные 0 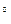или 180 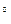. В диэлектрическом волноводе они являются сложными функциями, зависящими от диэлектрической и магнитной проницаемостей волновода и подложки, длины волны, размеров волновода и могут варьироваться в пределах 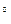0 …180 .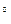

Амплитуды составляющих векторов 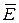и зависят от направляющих косинусов этих векторов.

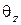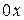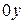Зная направляющие углы вектора Пойнтинга : , , и ориентацию векторов и нормально и параллельно поляризованных волн относительно выбранной плоскости , можно определить их направляющие косинусы относительно осей координат: , , . Для этого целесообразно ввести новую систему координат: , , 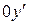, оси которой совпадают с направлением векторов , , .

Положение новой координатной системы относительно старой может быть полностью охарактеризовано тремя углами, введенными Л. Эйлером: углом нутации, углом прецессии и углом чистого вращения. С помощью этих углов можно определить направляющие косинусы векторов , и , .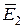

В соответствии с тремя вариантами расположения поляризационных базисов будут иметь место и три варианта направляющих косинусов.

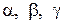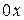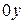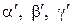Обозначим через – углы между вектором и осями координат , , ; – углы между вектором и теми же осями.

1. Плоскость S проходит через вектор и ось 0z.

Векторы и нормально поляризованной волны имеют следующие направляющие косинусы:

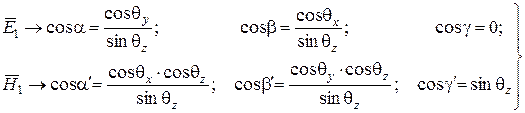. (6.9)

Направляющие косинусы векторов 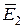и параллельно поляризованной волны определяются следующими выражениями:

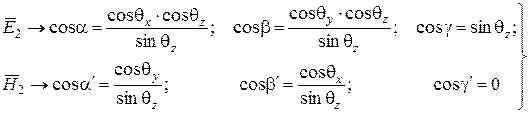. (6.10)

2. Плоскость проходит через вектор и ось .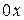

Для векторов , нормально поляризованной волны направляющие косинусы определяются выражениями:

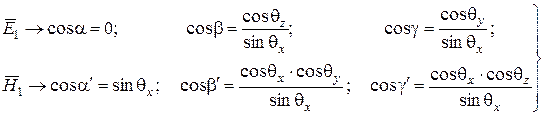. (6.11)

Для параллельно поляризованной волны:

. (6.12)

3. Плоскость проходит через вектор и ось .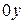

Для нормально поляризованной волны:

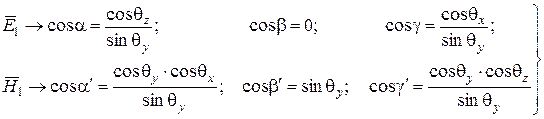. (6.13)

Для параллельно поляризованной волны:

. (6.14)

Направление вектора Пойнтинга определяется значениями углов , , 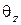с положительными направлениями осей координат.

Амплитуды составляющих векторов 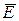и связаны с их амплитудными значениями соотношениями:

. (6.15)

Все эти амплитуды можно выразить через одну из них, например 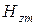, как это сделано при анализе магнитных волн 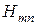в металлическом прямоугольном волноводе.

В этом случае

, (6.16)

где – волновое сопротивление среды, заполняющей волновод.

Подставляя 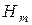и 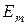из (6.16) в (6.15), получаем значения амплитуд всех составляющих, выраженные через . Направляющие косинусы при этом определяются выражениями (6.9):

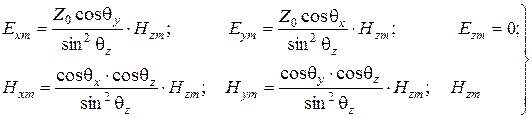. (6.17)

При анализе электрических волн 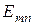амплитуды всех составляющих выражаются через , а направляющие косинусы определяются выражениями (6.10).

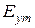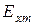В диэлектрическом и металлодиэлектрическом волноводах амплитуды составляющих волн типа связаны с и косинусами (6.11), а типа – с и косинусами (6.12).

В металлическом полом волноводе касательные составляющие вектора 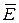и нормальные составляющие вектора равны нулю (считаем стенки идеально проводящими). Следовательно, фазы их коэффициентов отражения , равны 180 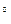. Нормальные составляющие вектора 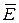и касательные составляющие вектора максимальны у граничных поверхностей, для них фазы коэффициентов отражения , равны нулю.

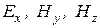На поверхности для составляющих имеем 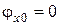, а для составляющих – .

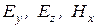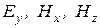На поверхности для составляющих имеем 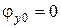, а для составляющих – .

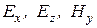Любая составляющая векторов 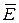и определяется выражением (6.8). Подставляя в него значения амплитуды (6.17) и учитывая значения фаз на поверхностях и , запишем выражения для составляющих векторов собственного поля :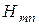

. (6.18)

Аналогичным образом можно найти составляющие векторов 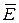и собственного поля :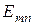

. (6.19)

В соответствие с выражением (6.8) распределение амплитуды любой составляющей вдоль оси 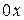описывается функцией

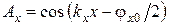. (6.20)

Тогда, при имеем 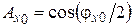, а при - . Но в то же время, при имеем , где – фаза коэффициента отражения на границе .

Равенство функций будет достигаться при следующем соотношении аргументов: . Откуда следует . Учитывая, что 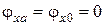, получаем

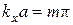. (6.21)

Из условия следует равенство функций , откуда также можно получить 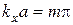, где

Из (6.21) следует, что . Учитывая соотношение 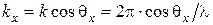, имеем

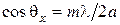. (6.22)

Аналогичным образом определяем

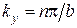, (6.23)

и направляющий косинус

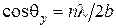, (6.24)

где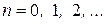

Из выражения (6.1) вытекает соотношение

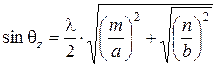. (6.25)

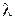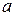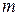Как видно из (6.22), (6.24), (6.25) направление вектора Пойнтинга зависит от длины волны , размеров волновода и , и от типа волны, который определяется индексами и 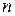, представляющими собой количество полуволн, укладывающихся на размерах 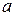и .

При увеличении длины волны 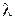, 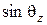увеличивается. А при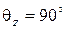 , и распространение электромагнитной волны вдоль волновода прекращается. Длина волны, при которой угол 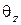достигает , соответствует критической длине волны.

Из (6.25)

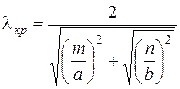, (6.26)

и , а 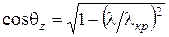. (6.27)

Выражения для амплитуд составляющих векторов 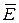и (6.18), (6.19) можно видоизменить, если умножить числитель и знаменатель на 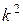, и учесть, что , , , , а также , , .

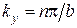Составляющие векторов поля типа :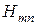

. (6.28)

Составляющие векторов поля типа :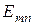

, (6.29)

где 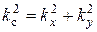– поперечное волновое число, – коэффициент распространения, – длина волны в волноводе.

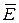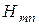Полученные выражения для составляющих векторов и собственных полей и 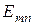на основе лучевых представлений полностью совпадают с выражениями, найденными путем анализа уравнений Максвелла. Указанное соответствие подтверждает правильность предположения о том, что собственные поля представляют собой ортогональные линейно поляризованные плоские волны, распространяющиеся в волноводе под определенными углами 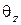к его оси.

Запишем выражения для составляющих векторов поля, когда поляризационный базис лежит в плоскости перпендикулярной плоскости , проходящей через вектор и ось 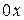(второй вариант). Для нормально поляризованной волны ( ) амплитуды составляющих выразим через 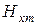. Учитывая выражения (6.15) и (6.11), получаем:

. (6.30)

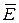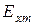Амплитуды составляющих векторов и параллельно поляризованной волны выражаем через , пользуясь (6.15) и (6.12):

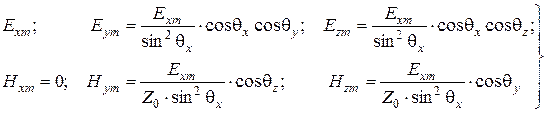. (6.31)

Пространственное распределение составляющих векторов поля и зависимости их от времени остаются такими же, как и в (6.28), (6.29). Видоизменяя (6.30) и (6.31) как и в предыдущем случае, запишем выражения для составляющих векторов 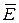и собственных полей и .

Так для 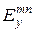получаем:

; (6.32)

; (6.33)

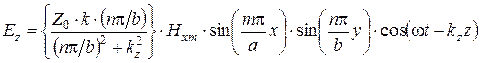; (6.34)

; (6.35)

; (6.36)

. (6.37)

Аналогично для :

; (6.38)

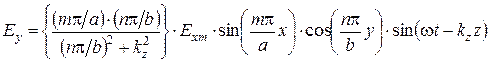; (6.39)

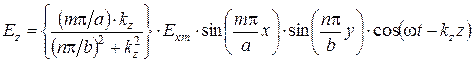; (6.40)

; (6.41)

; (6.42)

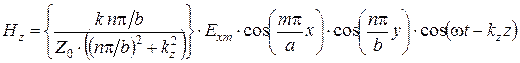. (6.43)

Простейший тип волны , как и волны , имеет три составляющие: Волне соответствует волна , у нее также три составляющие: Можно найти соответствие и другим типам волн.

Таким образом, подтверждается тезис о равноценности выбора варианта ориентации поляризационного базиса.

Дата добавления: 2014-10-10; просмотров: 536; Нарушение авторских прав

Мы поможем в написании ваших работ!