
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
Передаточные функции четырёхполюсников
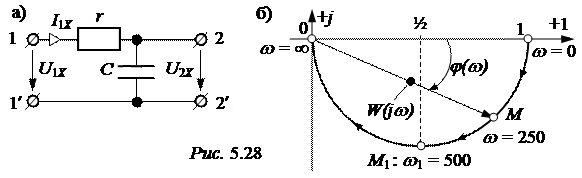
ЗАДАЧА 5.37. Для Г-схемы четырёхполюсника (рис. 5.28,а) рассчитать и построить частотные характеристики передаточной функции по напряжению в режиме холостого хода, если r = 50 Ом, С = 40 мкФ.
Решение
Искомую передаточную функцию можно рассчитать с помощью основных уравнений с коэффициентами любой формы, с помощью основных уравнений с характеристическими параметрами. Однако для простых схем четырёхполюсников эту работу проще выполнить с помощью законов
Кирхгофа, записав в комплексной форме выражения тока I1X и напряжения U2X в функции w : U2X = I1X · 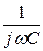 , а I1X =
, а I1X = 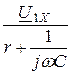 , тогда
, тогда
W(jw) = 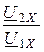 =
= 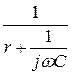 ·
· 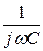 =
= 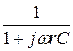 =
= 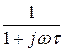 ,
,
 |
где t = rC = 50·40·10 -6 = 2·10 -3 c – называется постоянной времени рассматриваемого звена (четырёхполюсника) (см. раздел «Переходные процессы в линейных электрических цепях»), а передаточная функция приведённого вида W(jw) =
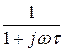 является передаточной функцией одного из типовых звеньев систем автоматического управления (САУ) – апериодического звена.
является передаточной функцией одного из типовых звеньев систем автоматического управления (САУ) – апериодического звена.
Диаграмма Найквиста этой передаточной функции приведена на рис. 5.28,б и представляет собой полуокружность радиуса R = ½. Изображающая точка М определяет положение конца вектора W(jw) на комплексной плоскости при фиксированных частотах:
при частоте w = 0 координатами точки М являются (1, 0);
при частоте w = 0,5·t -1 = 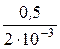 = 250
= 250 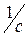
W(jw) = 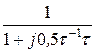 =
= 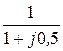 = 0,8 - j0,4,
= 0,8 - j0,4,
W(w) = 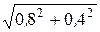 = 0,894, j(w) = arctg
= 0,894, j(w) = arctg 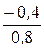 = -26,56°,
= -26,56°,
эта точка М указана на рис. 5.28,б.
Положение точки М1 соответствует частоте w = t -1 = 500 c -1, а при w = ¥ W(w) = 0, j(w) = -90° = -½p точка М оказывается в начале координат.
Заметим, что при изменении частоты w(0 … ¥) изображающая точка перемещается по часовой стрелке и фазовый угол для схемы с одним накопителем изменяется на 90°. Это является общим свойством диаграмм Найквиста, только фазовый угол при этом будет изменяться до (-n·½p), где n – число разнородных накопителей.
Амплитудная частотная характеристика W(w) = 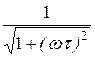 – чётная функция частоты, фазовая частотная характеристика j(w) = -arctg(wt) – нечётная функция, при этом размерность j(w) – радианы.
– чётная функция частоты, фазовая частотная характеристика j(w) = -arctg(wt) – нечётная функция, при этом размерность j(w) – радианы.
Вещественная и мнимая частотная характеристики рассчитываются по
W(jw) = 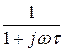 ·
· 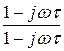 =
= 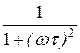 – j
– j 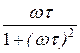 ,
,
где B(w) = 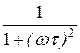 – вещественная частотная характеристика, чётная функция частоты,
– вещественная частотная характеристика, чётная функция частоты,
M(w) = - 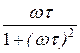 – мнимая частотная характеристика, нечётная функция частоты.
– мнимая частотная характеристика, нечётная функция частоты.
Заметим, что фазовую частотную характеристику можно также рассчитать как j(w) = arctg 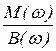 .
.
Логарифмическая амплитудная частотная характеристика
L(w) = 20lgW(w) = -20lg 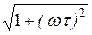 = -10lg
= -10lg 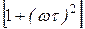 .
.
Результаты расчёта характеристик передаточной функции сведём в табл. 5.1.
Таблица 5.1
| w, c -1 | wt | 1+(wt)2 | W(w) | j(w), рад | L(w), дБ | lg(w) | B(w) | -M(w) |
| -¥ | ||||||||
| ¼t -1=125 | 0,25 | 1,063 | 0,97 | -0,245 | -0,264 | 2,09 | 0,94 | 0,235 |
| ½t -1=250 | 0,5 | 1,25 | 0,894 | -0,464 | -0,973 | 2,4 | 0,8 | 0,4 |
| 1t -1=500 | 0,707 | -0,785 | -3,01 | 2,7 | 0,5 | 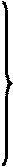 0,5 0,5
| ||
| 1,5t -1=750 | 1,5 | 3,25 | 0,555 | -0,983 | -5,12 | 2,88 | 0,31 | 0,462 |
| 2t -1=100 | 0,447 | -1,11 | -6,99 | 0,2 | 0,4 | |||
| 3t -1=1500 | 0,316 | -1,25 | -10 | 3,18 | 0,1 | 0,3 | ||
| 4t -1=2000 | 0,243 | -1,33 | -12,3 | 3,3 | 0,06 | 0,235 | ||
| 5t -1=2500 | 0,196 | -1,37 | -14,1 | 3,4 | 0,04 | 0,192 | ||
| 10t -1=5000 | 0,01 | -1,47 | -20,04 | 3,7 | 0,01 | 0,09 |
В табл. 5.1 фигурной скобкой отмечен диапазон частот, соответству-ющий декаде, у которой отличие частот w составляет в 10 раз, а отличие lg(w) – на единицу.
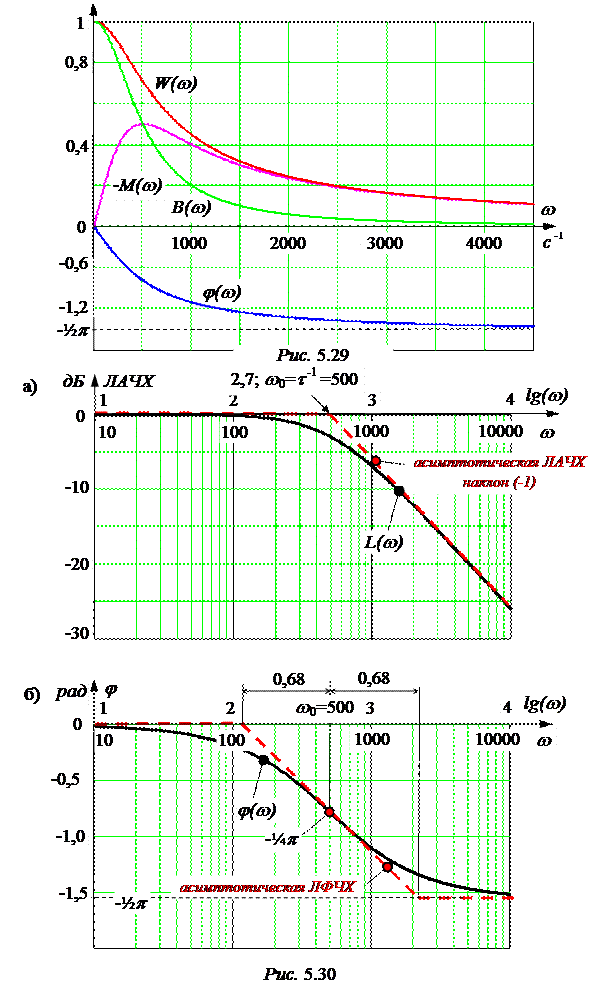
Характеристики W(w), B(w), -M(w), j(w) приведены на рис. 5.29.
Логарифмические амплитудные частотные характеристики приведены на рис. 5.30,а (сплошные линии), а их асимптотические характеристики вы-полнены отрезками прямых (штриховые линии). Частота сопряжения прямых линий w0 = t -1; максимальное отклонение асимптотических ЛАЧХ от факти-ческих составляет 3,01 дБ, угол наклона прямой составляет 20 дБ/декаду, что обычно обозначается как (-1) (соответственно, при 40 дБ/декаду будет (-2), при 60 дБ/декаду – (-3) и т.д.). ЛФЧХ приведена на рис. 5.30,б.
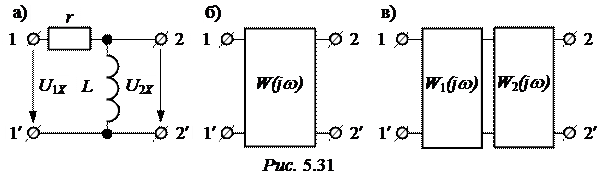 |
ЗАДАЧА 5.38. Для Г-схемы четырёхполюсника (рис. 5.31,а) при r = =50 Ом, l = 0,5 Гн. рассчитать частотные характеристики передаточной функции по напряжению в режиме холостого хода. Построить асимптотические логарифмические амплитудную (ЛАЧХ) и фазовую (ЛФЧХ) частотные характеристики.
Ответ: W(jw) = 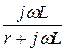 =
= 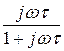 , где постоянная времени звена t =
, где постоянная времени звена t = 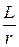 , структурная схема передачи сигнала приведена на рис. 5.31,б.
, структурная схема передачи сигнала приведена на рис. 5.31,б.
Передаточную функцию W(jw) можно представить как произведение двух передаточных функций W(jw) = W1(jw)·W2(jw). Этому произведению соответствует каскадное соединение двух четырёхполюсников (рис. 5.31,в), для которого W1(jw) = jwt – передаточная функция идеального дифферен-цирующего звена, а W2(jw) = 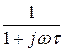 – передаточная функция апериодиче-ского звена, характеристики которого построены при решении задачи 5.37.
– передаточная функция апериодиче-ского звена, характеристики которого построены при решении задачи 5.37.
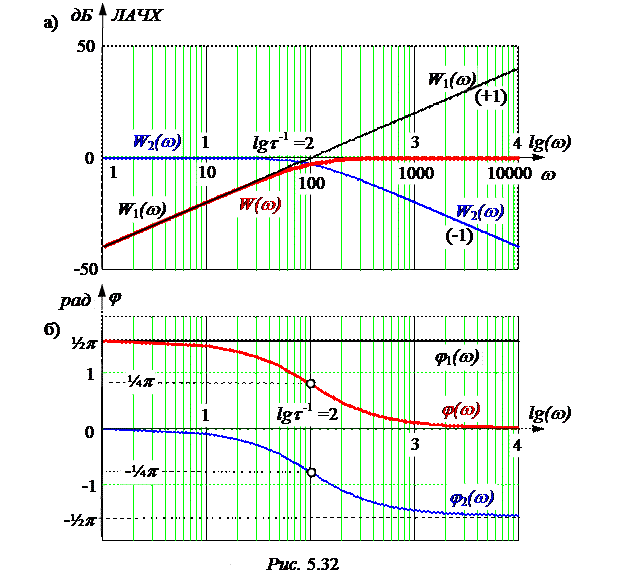
На рис. 5.32,а приведено построение ЛАЧХ функций W1(w), W2(w) и результирующей W(w), на рис. 5.32,б приведено построение логарифмиче-ской фазовой частотной характеристики.
ЗАДАЧА 5.39. Для Г-образного четырёхполюсника, нагруженного активным сопротивлением rН = 150 Ом (рис. 5.33), рассчитать передаточ-ную функцию по напряжению, если r = 50 Ом, С = 40 мкФ.
Ответ: W(jw) = 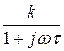 , где k =
, где k = 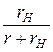 , t =
, t = 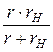 C.
C.

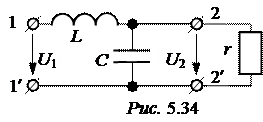 ЗАДАЧА 5.40. Для Г-образного четы-рёхполюсника, нагруженного активным сопротивлением r = 50 Ом (рис. 5.34), рассчитать передаточную функцию по напряжению, если L = 0,5 Гн, С = 40 мкФ.
ЗАДАЧА 5.40. Для Г-образного четы-рёхполюсника, нагруженного активным сопротивлением r = 50 Ом (рис. 5.34), рассчитать передаточную функцию по напряжению, если L = 0,5 Гн, С = 40 мкФ.
Построить асимптотические лога-рифмические частотные характеристики передаточной функции по напряжению.
Указание. При построении ЛАЧХ и ЛФЧХ представить четырёхполюсник исходной схемы в виде каскадного соединения двух апериодических звеньев с передаточными функциями W1(jw) = 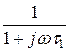 и W2(jw) =
и W2(jw) = 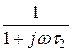 .
.
Ответ: W(jw) = 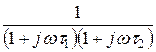 , где t1,2 =
, где t1,2 = 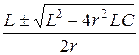 .
.
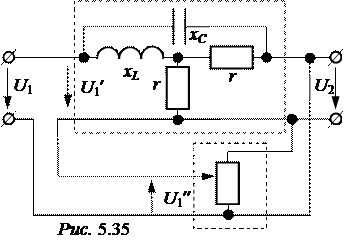 ЗАДАЧА 5.41. Задан четы-рёхполюсник с обратной связью (рис. 5.35): хL = 80 Ом, хС = 40 Ом, r = 40 Ом, U1 = 100 В,коэффи-циент обратной связи КОС = 0,2. Четырёхполюсник нагружен на сопротивлением Z2 = 20 Ом.
ЗАДАЧА 5.41. Задан четы-рёхполюсник с обратной связью (рис. 5.35): хL = 80 Ом, хС = 40 Ом, r = 40 Ом, U1 = 100 В,коэффи-циент обратной связи КОС = 0,2. Четырёхполюсник нагружен на сопротивлением Z2 = 20 Ом.
Определить выходное напряжение четырёхполюсника с обратной связью и без неё.
Пояснения к решению:для характеристики условий передачи сигналов с учётом произвольной нагрузки пользуются так называемыми рабочими параметрами, к которым относятся вносимое затухание аВН и коэффициенты передачи по напряжению KU и по току KI, которые ещё называют передаточными функциями четырёхполюсника H(jω).
Коэффициенты передачи четырёхполюсника по напряжению без обратной связи KU¢ и при наличии обратной связи KU¢¢ на основании основных уравнений четырёхполюсника определяются выражениями:
KU¢ = 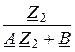 , KU¢¢ =
, KU¢¢ = 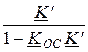 .
.
А-коэффициенты четырёхполюсника:
А = 1,2 – j0,6, В = 4 – j52 Ом, С = 0,01 – j0,005 См, D = 0,7 – j0,1.
Для четырёхполюсника без обратной связи при напряжении U1 = 100 В находим коэффициент передачи по напряжению и выходное напряжение:
KU¢ = 0,286 е j68,37°, U2 = KU¢·U1 = 28,6 е j68,37° В.
Коэффициент передачи четырёхполюсника при наличии обратной свя-зи:
KU¢¢ = 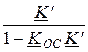 = 0,292е j71,48°.
= 0,292е j71,48°.
Напряжение на выходе: U2 = KU¢¢∙U1 = 29,2 е j71,48° В.
В связи с развитием вычислительной техники использование передаточных функций и характеристик для расчёта реакции цепи по известному воздействию произвольной формы становится актуальным. В задачах 5.42 и 5.43 на примере простейшего четырёхполюсника сделана попытка проиллюстрировать применение передаточных функций. При расчётах интенсивно использовалась математическая система MathCAD. К сожалению, имеются некоторые отличия в обозначении величин, функций и чисел в системе MathCAD от общепринятых математических обозначений. Так, комплексные величины не подчёркиваются, иначе представляются степени числа 10 в ответах, использование индексации символизирует числовой массив. Поэтому при решении задач приведены формулы как в общепринятом виде, так и фрагменты MathCAD-программы. На наш взгляд, отличия непринципиальные и на понимании решения не сказываются. В данном параграфе рассмотрены вопросы получения передаточных характе-ристик и их использования при гармоническом воздействии. Использование характеристик в случае других типов воздействий будет рассмотрено в по-следующих разделах «Цепи несинусоидального тока (при негармонических воздействиях)» и «Переходные процессы в линейных электрических цепях».
Различные величины в обобщённой цепи четырёхполюсника, подклю-ченного к источнику с ЭДС Е и внутренним сопротивлением Z1 и нагружен-ного сопротивлением Z2, могут быть вычислены через А-параметры:
- входное напряжение U1 = Е(А11Z2+ А12)/НA;
- входной ток I1 = Е(А21Z2+ А22)/НA;
- выходное напряжение U2 = Е·А12/НA;
- выходной ток I2 = -Е/НA.
Здесь НA = А11·Z2 + А22·Z1 + А12 + А21·Z1·Z2– вспомогательная частотная характеристика, выраженная через А-параметры четырёхполюсника. Отметим, что последовательно соединённые Е-Z1 могут быть заменены параллельно соединёнными J-Z1, то есть воздействие может быть как в виде напряжения Е, так и в виде тока J = Е/Z1. В этом случае приведенные формулы корректируются соответствующим образом.
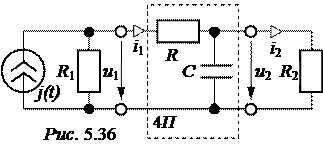
ЗАДАЧА 5.42. Источник, представленный схемой замещения j(t)-r1, питает нагрузку r2 через Г-образный безындукционный фильтр низкой частоты, являющийся пассивным четырёхполюсником (рис. 5.36). Числовые значения:
r1 = 5000 Ом, r2 = 2000 Ом, r = 1000 Ом, С = 10 мкФ.
Вычислить: 1) коэффициенты формы А четырёхполюсника; 2) опреде-лить комплексное передаточное сопротивление канала связи; 3) построить АЧХ и ФЧХ; 4) нарисовать диаграмму Найквиста; 5) пользуясь комплексным передаточным сопротивлением, определить выходное напряжение u2 для следующих случаев –
j(t) = 0,05 А, j(t) = 0,05·sin(100t + 45°) А,
j(t) = 0,05·sin(1000t – 100°) А, j(t) = 0,05·sin(10000t + 100°) А.
Решение
1. Обозначим сопротивления ветвей анализируемого четырёхполюсни-
ка как Z1 = r и Z2 = 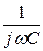 . Коэффициенты А-формы определяем по известным
. Коэффициенты А-формы определяем по известным
формулам Г-образного четырёхполюсника:
А11 = 1 + 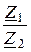 ; А12 = Z1; А21 =
; А12 = Z1; А21 = 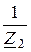 ; А22 = 1.
; А22 = 1.
Коэффициенты представим в функции частоты:
Z1(jw) := r Z2(jw) := 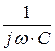
А11(jw) := 1+ 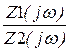 А11(jw)
А11(jw) 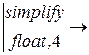 1.+.1000е-1·jw
1.+.1000е-1·jw
А12(jw) :=Z1(jw) А12(jw) 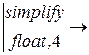 1000
1000
А21(jw) := 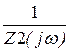 А21(jw)
А21(jw) 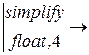 .1000е-4·jw
.1000е-4·jw
А22(jw) := 1 А22(jw) 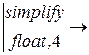 1
1
Проверка: А11(jw)·А22(jw) – А12(jw)·А21(jw) 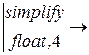 1.
1.
Таким образом, значения коэффициентов следующие:
А11 = 1 + 0,01·jw ; А12 = 1000 Ом; А21 = 10 -5·jw См; А22 = 1.
2. Входной величиной (воздействием) в данной задаче выступает j(t), выходной (реакцией) – напряжение на нагрузке u2(t). Поэтому комплексная передаточная функция (КПФ) Н(jw) = ХВЫХ(jw)/ХВХ(jw) здесь является комплексным передаточным сопротивлением, которое обозначим как
Z(jw) = U2(jw)/J(jw).
Вычислим Z(jw) двумя способами. В первом способе используются полученные коэффициенты формы А. Сначала вычисляем вспомогательную частотную функцию
НА(jw) := А11(jw)·r2 + А22(jw)·r1 + А12(jw) + А21(jw)·r1·r2
НА(jw) 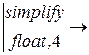 8000. + 120.·jw,
8000. + 120.·jw,
Искомое сопротивление
Z(jw) := 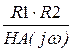 Z(jw)
Z(jw) 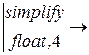
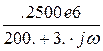 .
.
Выполним проверочный расчёт вторым способом, задавшись выход-ным напряжением u2 = 1 и определив входной ток J, используя законы Ома и Кирхгофа:
I1(jw) := 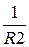 + jw ·C U1(jw) := 1 + r·I1(jw) J(jw) := I1(jw) +
+ jw ·C U1(jw) := 1 + r·I1(jw) J(jw) := I1(jw) + 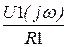
Z(jw) := 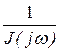 Z(jw)
Z(jw) 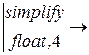
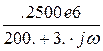 .
.
Таким образом, ответ для комплексного передаточного сопротивления следующий: Z(jw) = 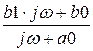 =
= 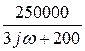 =
= 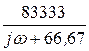 Ом.
Ом.
Значения коэффициентов в данной задаче:
b1 = 0, b0 = 83333, a0 = 66,67.
3. АЧХ и ФЧХ канала связи строятся в соответствии со следующими формулами:
Z(w) = |Z(jw)| = 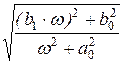 =
= 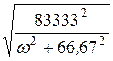 ;
;
j(w) = arg(Z(jw)) = arctg 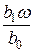 – arctg
– arctg 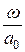 = arctg
= arctg 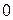 – arctg
– arctg 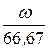 .
.
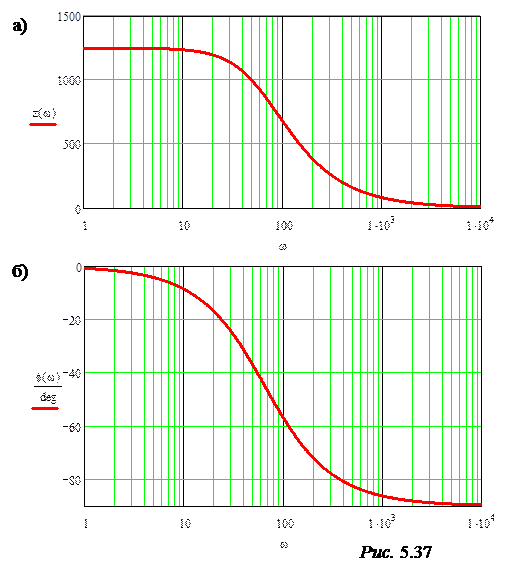
Графики АЧХ и ФЧХ приведены на рис. 5.37,а и б.
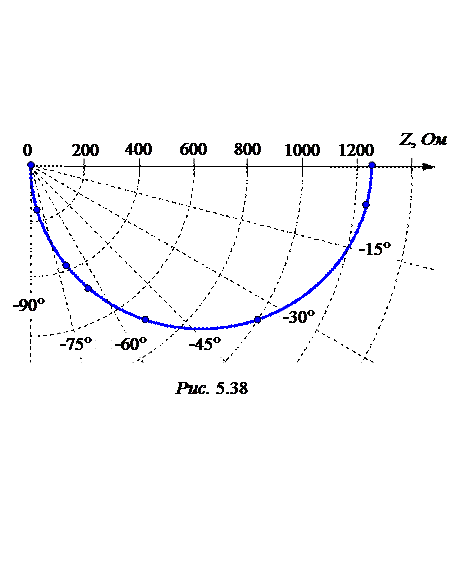
4. Диаграмма Найквиста представляет собой график зависимости Z(w) = f(j(w)) в полярной системе координат. Расчёты по построению графи-ка сведём в табл. 5.2. Сама диаграмма представлена на рис. 5.38.
Таблица 5.2
| w, с -1 | ¥ | ||||||||
| j, град | -8,5 | -36,9 | -56,3 | -66,0 | -71,6 | -82,4 | -86,2 | -90 | |
| Z, Ом | 507,7 | 165,2 | 83,1 |
 |
5. Значения комплексного передаточного сопротивления на заданных в условии задачи частотах следующие:
Z(0) = 1250 Ом, Z(j100) = 693,4·е –j56,31° Ом,
Z(j1000) = 83,15·е –j86,19° Ом, Z(j10000) = 8,33·е –j89,62° Ом.
Комплексные амплитуды воздействия J(jw)
и реакции U2(jw) = Z(jw)·J(jw) на этих же частотах:
J(0) = 0,05 А, J(j100) = 0,05·е j45° А,
J(j1000) = 0,05·е –j100° А, J(j10000) = 0,05·е j100° А,
U2(0) = 62,5 В, U2(j100) = 34,7·е –j11,31° В,
U2(j1000) = 4,16·е j173,81° В, U2(j10000) = 0,42·е j10,38° В.
 Мгновенные значения выходного напряжения:
Мгновенные значения выходного напряжения:
u2(t) = 62,5 В, u2(t) = 34,7·sin(100t – 11,31°) В,
u2(t) = 4,16·sin(1000t + 173,81°) В, u2(t) = 0,42·sin(10000t + 10,38°) В.
Обращаем внимание на то, как стремительно убывают амплитуды напряжения u2 с ростом частоты при том, что амплитуда воздействия сохраняется неизменной 0,05 А. Здесь проявляются фильтрующие свойства рассматриваемого четырёхполюсника.
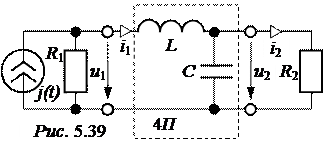
ЗАДАЧА 5.43. Решить задачу 5.42 после замены резистора r ин-дуктивностью L = 10 Гн (рис. 5.39). Значение ёмкости взять равным С = 1 мкФ.
Решение
Порядок решения задачи 5.43 тот же, что и задачи 5.42. Поэтому приведём ответы.
1. Z1(jw) := jw ·L Z2(jw) := 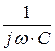
А11(jw) := 1+ 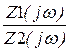 А11(jw)
А11(jw) 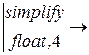 1.+.1000е-4·(jw)2
1.+.1000е-4·(jw)2
А12(jw) :=Z1(jw) А12(jw) 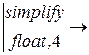 10.·jw
10.·jw
А21(jw) := 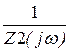 А21(jw)
А21(jw) 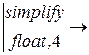 .1000е-5·jw
.1000е-5·jw
А22(jw) := 1 А22(jw) 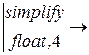 1
1
Проверка: А11(jw)·А22(jw) – А12(jw)·А21(jw) 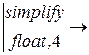 1.
1.
Таким образом, значения коэффициентов следующие:
А11 = 1 + 10 -5·(jw)2; А12 = 10jw Ом; А21 = 10 -6·jw См; А22 = 1.
2. Первый способ вычисления Z(jw).
НА(jw) := А11(jw)·r2 + А22(jw)·r1 + А12(jw) + А21(jw)·r1·r2
НА(jw) 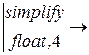 7000. + .2000е-1·(jw)2 + 20.·jw,
7000. + .2000е-1·(jw)2 + 20.·jw,
Z(jw) := 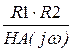 Z(jw)
Z(jw) 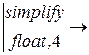
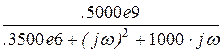 .
.
Второй способ вычисления Z(jw).
I1(jw) := 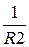 + jw ·C U1(jw) := 1 + Z1(jw)·I1(jw) J(jw) := I1(jw) +
+ jw ·C U1(jw) := 1 + Z1(jw)·I1(jw) J(jw) := I1(jw) + 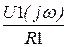
Z(jw) := 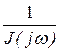 Z(jw)
Z(jw) 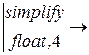
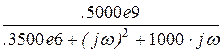 .
.
Таким образом, ответ для комплексного передаточного сопротивления следующий: Z(jw) = 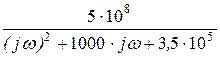 Ом.
Ом.
3. АЧХ и ФЧХ канала связи строятся в соответствии со следующими формулами:
Z(w) := 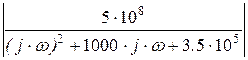 ;
;
j(w) := arg 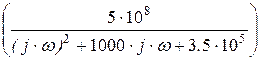 .
.
Графики АЧХ и ФЧХ приведены на рис. 5.40,а и б.
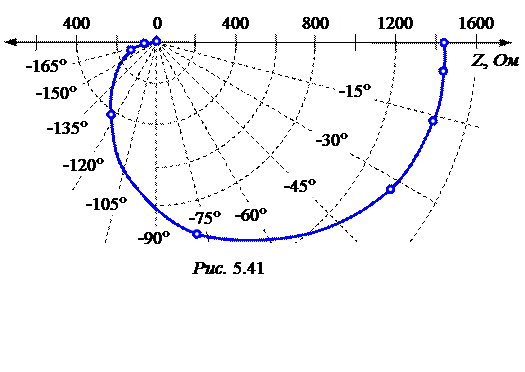
4. Расчёты по построению диаграммы Найквиста сведём в табл. 5.3. Сама диаграмма представлена на рис. 5.41.
Таблица 5.3
| w, с -1 | ¥ | ||||||||
| j, град | -8,19 | -16,39 | -32,83 | -78,69 | -123,0 | -151,3 | -168,5 | -180 | |
| Z, Ом | 19,9 |
 |
5. Значения комплексного передаточного сопротивления на заданных в условии задачи частотах следующие:
Z(0) = 1429 Ом, Z(j100) = 1411·е –j16,39° Ом,
Z(j1000) = 419,2·е –j123,02° Ом, Z(j10000) = 4,99·е –j174,27° Ом.
Комплексные амплитуды воздействия J(jw)
и реакции U2(jw) = Z(jw)·J(jw) на этих же частотах:
J(0) = 0,05 А, J(j100) = 0,05·е j45° А,
J(j1000) = 0,05·е –j100° А, J(j10000) = 0,05·е j100° А,
U2(0) = 71,43 В, U2(j100) = 70,54·е j28,61° В,
U2(j1000) = 20,96·е j136,98° В, U2(j10000) = 0,25·е -j74,27° В.
Мгновенные значения выходного напряжения:
u2(t) = 71,43 В, u2(t) = 70,54·sin(100t + 28,61°) В,
u2(t) = 20,96·sin(1000t + 136,98°) В, u2(t) = 0,25·sin(10000t – 74,27°) В.
Обращаем внимание на то, как стремительно убывают амплитуды напряжения u2 с ростом частоты, начиная с 500 рад/с. Здесь проявляются фильтрующие свойства рассматриваемого четырёхполюсника.
[1] Здесь и далее в скобках приведены встречающиеся в литературе альтернативные обозначения и названия.
| <== предыдущая страница | | | следующая страница ==> |
| Соединения четырёхполюсников | | | Интерпретация собственных полей прямоугольного волновода и его модификаций |
Дата добавления: 2014-10-10; просмотров: 525; Нарушение авторских прав

Мы поможем в написании ваших работ!