Длина отрезка прямой и углы наклона прямой к плоскостям проекции. Способ прямоугольного треугольника

Отрезок прямой, параллельной какой-либо плоскости проекции, проецируется на данную плоскость без искажения (в натуральную величину) (рис. 4.6, а и 4.6, б).

Так, отрезок АВ параллелен плоскости П₁(рис. 4.6, а),следовательно, длина отрезка равна его горизонтальной проекции A₁B₁. Угол βмежду осью хи горизонтальной проекцией отрезка определяет угол наклона отрезка АВ к плоскости П₂.

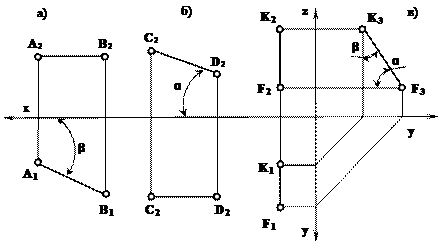Рис. 4.6

Отрезок CD параллелен плоскости П₂(рис. 4.6, б),следовательно, длина отрезка равна длине его фронтальной проекции C₂D₂.Угол αопреде­ляет угол наклона отрезка CD к плоскости П₁.

Отрезок KFпараллелен плоскости П₃(рис. 4.6, в), следовательно, длина отрезка равна длине его профильной проекции K₃F₃.Углы наклона отрезка к плоскостям П₁и П₂ определяют соответственно углы αи β.

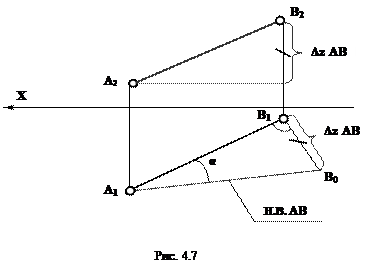
Если отрезок не параллелен плоскостям проекций, то для определения его натуральной величины и угла наклона к плоскостям проекций необходимо выполнить дополнительные построения: построить вспомогательный прямоугольный треугольник, один катет которого равен проекции отрезка на плоскость П₁или П₂, а другой - разности координат концов отрезка с другой проекции.

Так на рис. 4.7 один катет вспомогательного треугольника равен горизонтальной проекции отрезка A₁B₁а другой – В₁B₀ - разности координат z концов отрезка (точек А и В) В₂В₁. Гипотенуза А₁В₀определяет действительную длину отрезка АВ. Угол α при вершине A₁ определяет угол наклона отрезка АВ к плоскости П₁.

Дата добавления: 2014-04-19; просмотров: 894; Нарушение авторских прав

Мы поможем в написании ваших работ!