Студопедия

Главная страница Случайная лекция


Мы поможем в написании ваших работ!

Порталы:

БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика



Мы поможем в написании ваших работ!




Лекция № 14 Числовая последовательность. Сходящиеся и расходящиеся последовательности. Основные теоремы о пределе последовательности

Читайте также:
  1. I. ОПРЕДЕЛЕНИЕ БИОТЕХНОЛОГИИ КАК НАУКИ И ЕЕ ПРЕДМЕТА ИЗУЧЕНИЯ.
  2. I. Основные принципы и идеи философии эпохи Просвещения.
  3. IFRS 13 «Оценка по справедливой стоимости»: сфера применения стандарта, методы определения справедливой стоимости.
  4. II. ОСНОВНЫЕ ФАКТОРЫ РАДИАЦИОННОЙ ОПАСНОСТИ И МЕДИЦИНСКИЕ ПОСЛЕДСТВИЯ ОТ ИХ ВОЗДЕЙСТВИЯ НА ОРГАНИЗМ.
  5. II. Основы определения страхового тарифа.
  6. II. РАСПРЕДЕЛЕНИЕ ЛЕКАРСТВЕННЫХ СРЕДСТВ В ОРГАНИЗМЕ. БИОЛОГИЧЕСКИЕ БАРЬЕРЫ. ДЕПОНИРОВАНИЕ
  7. III. Основные политические идеологии современности.
  8. IV. Распределение часов курса по темам и видам работ
  9. IV.5. Основные тенденции развития позднефеодальной ренты (вторая половина XVII—XVIII в.)
  10. V. АКУСТИЧЕСКИЕ СВОЙСТВА ГОРНЫХ ПОРОД И МАССИВОВ. ОСНОВНЫЕ ФАКТОРЫ, ВЛИЯЮЩИЕ НА АКУСТИЧЕСКИЕ СВОЙСТВА ГОРНЫХ ПОРОД

Числовую функцию 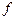, областью определения которой является множество натуральных чисел , называют функцией натурального аргумента или числовой последовательностью. В общем виде числовую последовательность (или просто последовательность) обозначают символом или .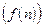

Для последовательностей важны два способа задания :

1. Аналитический, т.е. с помощью формулы 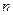-го члена вида .

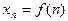2. Рекуррентный: задают один или несколько первых членов последовательности и формулу, позволяющую определить любой член последовательности по известным предыдущим членам.

Числовые последовательности как функции могут быть ограниченными сверху (снизу), неограниченными, монотонными и немонотонными. Но не имеет смысла ставить вопрос о четности или нечетности последовательности, так как множество 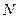не является симметричным.

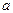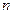
Числовую последовательность называют сходящейся к числу , если для любого числа > 0 найдется номер N такой что при всех выполняется неравенств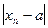о < . Число 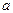при этом называют пределом последовательности (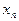) и обозначают символом 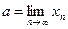. В символах математической логики определение того, что 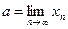запишется так: .

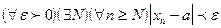Последовательность называется расходящейся к плюс (минус) бесконечности, если для любого числа Е найдется такой номер N, что при всех 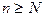выполняется неравенство . Обозначение : .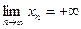

К основным теоремам о пределе последовательности относят следующие теоремы.

Теорема 1. Если последовательность имеет предел, то он единственный.

Теорема 2. Всякая сходящаяся последовательность ограничена.

Теорема 3. Всякая монотонная ограниченная последовательность имеет предел.

Теорема 4. Если последовательность сходится к числу 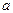, а

последовательность 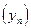сходится к числу 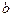и при этом ,

то .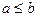

Теорема 5. Пусть даны три последовательност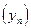и ,итакие, что

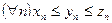. Если , то .

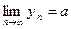Последовательность 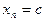, где некоторое число, называют постоянной. Все ее члены равны 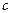. Очевидно, что такая последовательность является ограниченной и сходящейся. Ее пределом является число : .

 

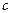<== предыдущая страница | следующая страница ==>
Лекция № 13 Основные элементарные функции: постоянная, степенная, показательная, логарифмическая, тригонометрические, обратные тригонометрические функции | Лекция № 15 Бесконечно малые и бесконечно большие последовательности и их свойства. Неопределенности. Число е

Дата добавления: 2014-03-19; просмотров: 673; Нарушение авторских прав



Мы поможем в написании ваших работ!
lektsiopedia.org - Лекциопедия - 2013 год. | Страница сгенерирована за: 0.003 сек.