
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
Лекция № 15 Бесконечно малые и бесконечно большие последовательности и их свойства. Неопределенности. Число е
Определение 1. Последовательность 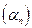 называют бесконечно малой,
называют бесконечно малой,
если 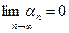
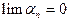 (т.е. если
(т.е. если 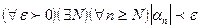
Теорема 1. Чтобы последовательность  сходилась к числу
сходилась к числу 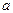 , необходимо и
, необходимо и
достаточно чтобы последовательность 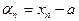 была бесконечно
была бесконечно
малой.
Теорема 2. Сумма двух бесконечно малых последовательностей является
бесконечно малой последовательностью.
Замечание. Легко заметить, что эту теорему можно обобщить на любое конечное число слагаемых. Например, для доказательства, что сумма трех бесконечно малых последовательностей является бесконечно малой последовательностью, достаточно дважды применить теорему 2.
Теорема 3. Если 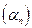 является бесконечно малой последовательностью, а
является бесконечно малой последовательностью, а  -
-
ограниченная последовательность, то 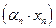 есть бесконечно малая
есть бесконечно малая
последовательность.
Следствие 1. Если 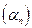 - бесконечно малая последовательность, а
- бесконечно малая последовательность, а 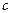 - некоторое
- некоторое
действительное число, то 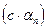 является бесконечно малой
является бесконечно малой
последовательностью.
Следствие 2. Произведение конечного числа бесконечно малых
последовательностей является бесконечно малой
последовательностью.
Следствие 3. Если  -
- 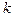 бесконечно малых последовательностей, а
бесконечно малых последовательностей, а
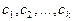 - действительные числа, то последовательность
- действительные числа, то последовательность
 является бесконечно малой.
является бесконечно малой.
Определение 2. Последовательность  называют бесконечно большой,
называют бесконечно большой,
если 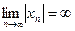 , т.е. если
, т.е. если 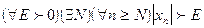
Теорема 4. Чтобы последовательность  была бесконечно большой,
была бесконечно большой,
необходимо и достаточно чтобы последовательность 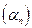 , где
, где
 , была бесконечно малой.
, была бесконечно малой.
Теорема 5. Если последовательности  и
и 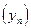 сходятся к числам
сходятся к числам 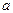 и
и 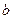
соответственно, то
1) последовательность 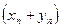 сходится к числу
сходится к числу  ;
;
2) последовательность 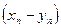 сходится к числу
сходится к числу  ;
;
3) последовательность 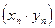 сходится к числу
сходится к числу 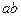 .
.
Теорема 6. Если последовательность  сходится к числу
сходится к числу 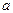 ;
;
последовательность 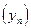 сходится к числу
сходится к числу 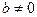 , то
, то
последовательность  сходится к числу
сходится к числу 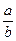 .
.
Неопределенностями называют пределы некоторых последовательностей, которые в зависимости от конструкции последовательностей могут принимать различные значения или не существовать. К неопределенностям относят  , если
, если 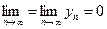 (неопределенность типа
(неопределенность типа  );
);  , если
, если 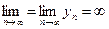 (неопределенность типа
(неопределенность типа 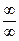 );
);  , если
, если  (неопределенность типа
(неопределенность типа  );
); 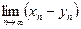 , если
, если 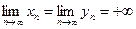 или
или 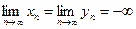 (неопределенность типа
(неопределенность типа 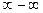 );
); 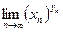 , где
, где 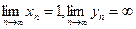 (неопределенность типа
(неопределенность типа  );
); 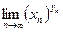 , где
, где 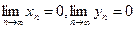 (неопределенность типа
(неопределенность типа  );
); 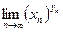 , где
, где 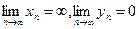 (неопределенность типа
(неопределенность типа  )
)
Последовательность 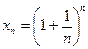 ограничена сверху и монотонно возрастает, а, следовательно, сходится. Предел этой последовательности принято обозначать буквой
ограничена сверху и монотонно возрастает, а, следовательно, сходится. Предел этой последовательности принято обозначать буквой 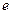 .
.

Число 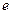 - иррациональное; его можно представить в виде бесконечной непериодической десятичной дроби:
- иррациональное; его можно представить в виде бесконечной непериодической десятичной дроби: 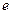 = 2,718281828459045...
= 2,718281828459045...
Это число часто принимают за основание степени, а показательную функцию 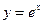 называют экспонентой. Логарифм числа
называют экспонентой. Логарифм числа 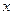 по основанию
по основанию 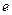 называют натуральным логарифмом и обозначают
называют натуральным логарифмом и обозначают 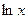 .
.
Дата добавления: 2014-03-19; просмотров: 560; Нарушение авторских прав

Мы поможем в написании ваших работ!