Коррелированные и зависимые случайные величины

Две случайные величины Х и У называются коррелированными если корреляционный момент или коэффициент корреляции отличен от нуля и Х,У - некоррелированные если и корреляционный момент равен нулю. Две коррелированные величины так же являются зависимыми величинами, обратное предположение не всегда имеет место, т.е. если две величины зависимы они могут быть как коррелированные так и некоррелированные. Другими словами, корреляционный момент двух зависимых величин может быть как равным нулю, так и не равным нулю. Итак, из корреляции двух случайных величин следует их зависимость, но из зависимости не следует их коррелированность . из независимости следует некоррелированность, но из некоррелированности не следует независимость.

Нормальным законом распределения называют распределение вероятностей двух случайных величин Х, У, если плотность распределения имеет вид

(**)

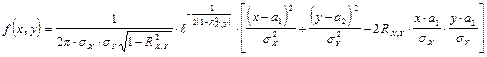Очевидно, что нормальный закон на плоскости определяется параметрами 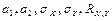. Можно убедится в том, что если составлять двумерное нормальное распределение случайной величины некоррелированное, то они независимы. Если составлять нормальное распределение случайной величины некоррелированное. То плотность совместного распределения системы равна произведению плотности распределенного состояния

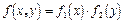
Отсюда следует независимость состава. Справедливо и обратное утверждение. Итак, для нормального распределения составляют двумерную случайную величину понятия независимость и некоррелированность равносильны.

Дата добавления: 2014-02-26; просмотров: 1144; Нарушение авторских прав

Мы поможем в написании ваших работ!