
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
Ковариация
Лекция 13. Корреляция и регрессия.
В предыдущем параграфе были рассмотрены условие распределение случайных величин, если условный закон распределения одной величины изменяется в зависимости от значений принимаемой другой случайной величиной, такую взаимосвязь называют стохастической или вероятностной. Одной из характеристик стохастической взаимосвязи двух случайных величин называют ковариационной случайной величиной.
Определение: ковариационной случайной величиной 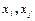 или корреляционным моментом называют число
или корреляционным моментом называют число 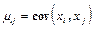 , равное математическому ожиданию произведения отношения случайной величины (
, равное математическому ожиданию произведения отношения случайной величины (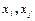 ) от своих математических ожиданий.
) от своих математических ожиданий.
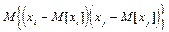 ( * )
( * )
Ковариацию называют так же вторым смешанным центральным моментом случайной величины 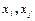 .
.
Кроме (*) ковариацию можно вычислить так же:
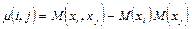
Из свойств математического ожидания следует, что:
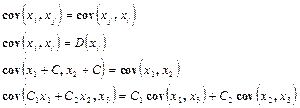
Ковариационная матрица случайного вектора 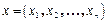 называется матрица элементов которой является
называется матрица элементов которой является 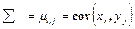
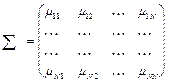
Из свойств ковариации следует, что ковариационная матрица является симметричной 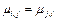 . Диагональные элементы равны дисперсии случайной величины, т.е.
. Диагональные элементы равны дисперсии случайной величины, т.е. 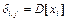 . Детерминированной
. Детерминированной 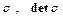 называется дисперсия которую можно использовать как меру рассеивания n- мерной случайной величины.
называется дисперсия которую можно использовать как меру рассеивания n- мерной случайной величины.
Ковариационная матрица и вектор средних 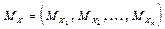 , являются основными числовыми характеристиками случайного вектора х. Если случайная величина
, являются основными числовыми характеристиками случайного вектора х. Если случайная величина 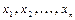 независимы, то вне диагонали элементы равны нулю
независимы, то вне диагонали элементы равны нулю
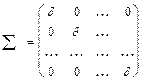
В качестве количественной характеристики зависимости случайно величины 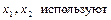 коэффициент корреляции
коэффициент корреляции 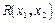 . Равный ковариационный момент случайной величины
. Равный ковариационный момент случайной величины
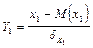
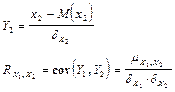
Корреляционная матрица случайного вектора х равна (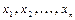 ) называется матрицей R элементами которой являются коэффициенты корреляции,
) называется матрицей R элементами которой являются коэффициенты корреляции, 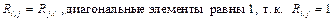
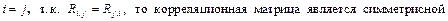
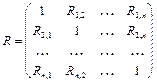
| <== предыдущая страница | | | следующая страница ==> |
| Свойства | | | Коррелированные и зависимые случайные величины |
Дата добавления: 2014-02-26; просмотров: 641; Нарушение авторских прав

Мы поможем в написании ваших работ!