Линейная регрессия. Прямые линии среднеквадратичной регрессии

Рассмотрим двумерную случайную величину (Х,У), где Х,У зависимые случайные величины, представим одну из величин как функцию другой. Ограничимся приближенным представлением величины У в виде линейной функцией от Х

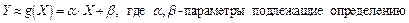
Это можно сделать различными способами ( метод наименьших квадратов ).

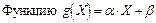называют наилучшим приближением У в смысле метода наименьших квадратов, если 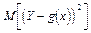принимает наименьшее возможное значение. Функция g(X) называется среднеквадратичной регрессией У на Х. Имеет место следующая теорема: линейная среднеквадратичная регрессия У на Х имеет вид

,

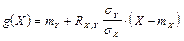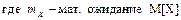
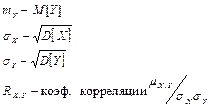
Можно убедиться, что коэффициент 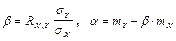. При этих значениях коэффициентов значение функции наименьшее. Прямая 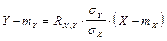(1) - прямая среднеквадратичной регрессии У на Х, а коэффициент 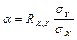-коэффициент регрессии У на Х. Прямая среднеквадратичной регрессии Х на У имеет вид:

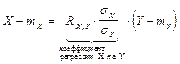(2)

При 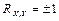обе прямые регрессии совпадают. Из (1) и (2) следует, что обе прямые регрессии проходят через точку 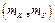которую называют центром совместного распределения.

Лекция 14. Корреляционный анализ.

Дата добавления: 2014-02-26; просмотров: 699; Нарушение авторских прав

Мы поможем в написании ваших работ!