Линейная и нормальная корреляция

Рассмотрим двумерную случайную величину (Х,Y), если обе функции регрессии YХ и ХY связанны линейной корреляционной зависимостью. Графики линейных функций регрессии–прямые линии, причем можно доказать, что они совпадают с прямыми среднеквадратичной регрессии.

Теорема. Если двумерная случайная величина (Х,Y) распределена нормально, то Х и Y связаны линейной корреляционной зависимостью.

Доказательство: двумерная плотность вероятности 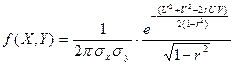, (1)

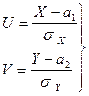где (2)

Плотность вероятности составляющей Х: 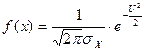. (3)

Найдем функцию регрессии 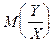, для чего найдем сначала условный закон распределения величины Y, при Х=х.

.

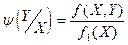Подставив соотношения (1) и (3) в правую часть этой формулы и упростим это выражение, имеем: 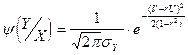. Заменив U и V по формулам (2), окончательно получим:

.

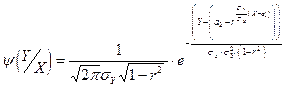Полученное условное распределение нормально с мат. ожиданием (функцией регрессии): 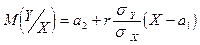и дисперсией .

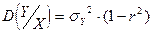Аналогично можно получить функцию регрессии :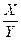

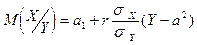
Так как обе функции линейны, то корреляция между величинами х и y– линейная, что и требовалось доказать. Отсюда делаем вывод, что уравнение прямых регрессии:

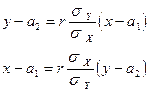
совпадают с кривыми среднеквадратичных.

Дата добавления: 2014-02-26; просмотров: 696; Нарушение авторских прав

Мы поможем в написании ваших работ!