Оценка корреляции и регрессионной характеристики по выборке

Для случайного вектора (X,Y) выборка, объема n дает n пар значений признака:

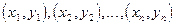. В этом случае говорят о связной выборке, в противоположность независимым выборкам, где совершенно независимо друг от друга наблюдается 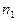значений х и 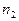значений y.

Для прямых регрессии могут быть даны оценки. Другими словами: теоретически характеристики регрессии могут быть оценены по выборке.

По функциям выборки получаются следующие характеристики (оценки).

Для ковариации (корреляционного момента) получают в качестве оценки эмпирическую ковариацию. .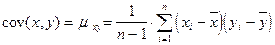

Отсюда получают оценки для теоретической корреляции и регрессионных характеристик. Например, эмпирический коэффициент корреляции имеет вид: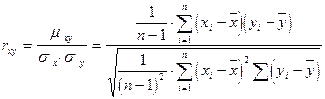

Аналогично получим эмпирические коэффициенты регрессии:

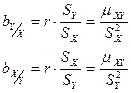
Эмпирические прямые регрессии будут иметь вид:

.

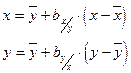При приблизительно коррелированных Х и Y можно сделать наилучшие предсказания для у при данном значении х или наилучшее предсказание для х при данном значении у.

Вопрос о том, имеется ли приблизительно линейная корреляция между х и у, только в редких случаях может быть решен теоретически. Это удается, если известно, что х и у распределены нормально, тогда линии регрессии являются прямыми, т.е. имеется точная линейная корреляция.

Дата добавления: 2014-02-26; просмотров: 619; Нарушение авторских прав

Мы поможем в написании ваших работ!