
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
Анализ автокорреляции остатков
Выше приведен пример определения взаимосвязи между показателями 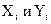 , составляющих два динамических ряда:
, составляющих два динамических ряда:
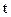
| |||||||
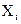
| 2,2 | 2,8 | 3,2 | 3,6 | 4,1 | 4,8 | 5,2 |
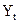
| 4,8 | 5,6 | 6,2 | 6,6 | 7,3 | 8,1 | 8,8 |
Каждый из показателей имеет высокий коэффициент автокорреляции 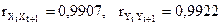 .
.
Это можно было также наблюдать и визуально.
После устранения трендов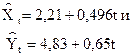
с помощью метода наименьших квадратов были получены остатки 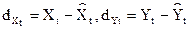 .
.
В соответствии с предпосылками метода наименьших квадратов их сумма и среднее значение равно нулю. Тогда для определения величины автокорреляции остатков наряду с непосредственным определением коэффициента автокорреляции можно использовать критерий Дарбина-Уотсона:
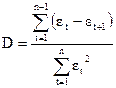 ,
,
где 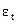 - остатки,
- остатки,
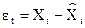 (
(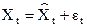 )
)
Коэффициент D связан с коэффициентом автокорреляции следующим образом, коэффициент автокорреляции можно записать в виде:
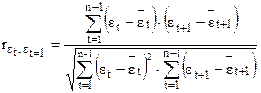 ,
,
где 
Так как, исходя из предпосылок метода наименьших квадратов, сумма и среднее значение остатков равны нулю, т. е.
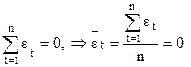 , то можно считать, что и
, то можно считать, что и 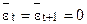 . Предположим также, что
. Предположим также, что 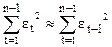 .
.
Тогда формула для расчета автокорреляции остатков преобразуется следующим образом:
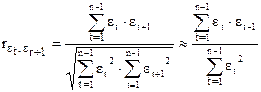 .
.
Теперь преобразуем формулу для расчета D:
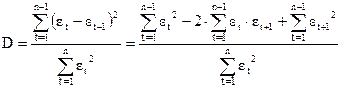 .
.
С учетом того, что 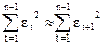 получим
получим
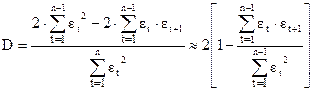
(где считаем, что 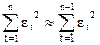 ввиду малости и большого числа остатков).
ввиду малости и большого числа остатков).
Следовательно, 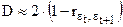 , тогда:
, тогда:
§ Если в остатках существует полная положительная автокорреляция и 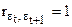 , то
, то 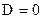 ;
;
§ Если в остатках полная отрицательная автокорреляция и 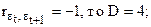
§ Если автокорреляция отсутствует, т.е. 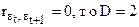 .
.
Следовательно, 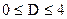 .
.
Поэтому автокорреляция остатков на основе критерия Дарбина-Уотсона выявляется следующим образом:
1. Выдвигается гипотеза 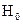 , об отсутствии автокорреляции остатков. Альтернативные гипотезы
, об отсутствии автокорреляции остатков. Альтернативные гипотезы  состоят в наличии положительной или отрицательной автокорреляции остатков.
состоят в наличии положительной или отрицательной автокорреляции остатков.
2. Вычисляется величина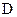 .
.
3. По специальным таблицам определяются критические значения критерия 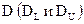 для заданного числа наблюдений
для заданного числа наблюдений  , числа независимых переменных модели
, числа независимых переменных модели 
K и уровня значимости 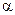 . По этим значениям числовой промежуток от 0 до 4 разбивается на 5 отрезков. Принятие или отклонение каждой из гипотез с вероятностью (
. По этим значениям числовой промежуток от 0 до 4 разбивается на 5 отрезков. Принятие или отклонение каждой из гипотез с вероятностью (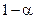 ) рассматривается на рисунке:
) рассматривается на рисунке:
|
На практике попадание в зону неопределенности трактуется как наличие автокорреляции и является основой для отклонения гипотезы 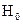 .
.
Рассмотрим в качестве примера остатки 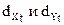 (см. пример).
(см. пример).
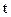
| Сумма | |||||||
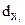
| -0,01 | 0,09 | -0,003 | -0,10 | -0,096 | 0,11 | 0,011 | 0,00002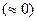
|
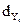
| -0,03 | 0,12 | 0,075 | -0,17 | -0,12 | 0,03 | 0,09 | 0,00001
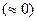
|
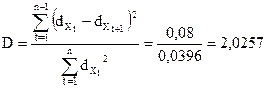 ,
, 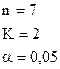
где
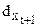
| 0,09 | -0,003 | -0,10 | -0,096 | 0,11 | 0,011 |
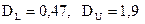
Таким образом справедлива гипотеза 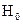 , т. е. автокорреляция остатков отсутствует.
, т. е. автокорреляция остатков отсутствует.
 |
Действительно, 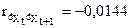 - небольшая отрицательная корреляция.
- небольшая отрицательная корреляция.
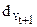
| 0,12 | 0,075 | -0,17 | -0,12 | 0,03 | 0,09 |
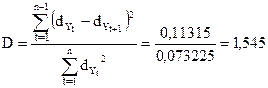 ,
, 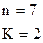
 |
Т. е. следует скорее принять гипотезу 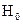 , т. е. попали в зону неопределенности. В действительности
, т. е. попали в зону неопределенности. В действительности 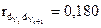 - положительная корреляция.
- положительная корреляция.
Отсюда видно, что критерий Дарбина-Уотсона очень чувствителен к величине автокорреляции.
При изучении взаимосвязи показателей по временным рядам остатки всегда проверяются на наличие автокорреляции, так как если эту автокорреляцию не учитывать, оценки уравнения регрессии могут быть неэффективными (хотя на свойства состоятельности и несмещенности автокорреляции остатков не влияет).
| <== предыдущая страница | | | следующая страница ==> |
| Временные ряды с детерминированными зависимостями | | | Иллюстрирующий проблему автокорреляции |
Дата добавления: 2014-03-19; просмотров: 915; Нарушение авторских прав

Мы поможем в написании ваших работ!
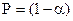 ,принимается
,принимается 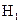
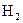
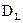
 2
2 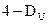
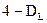 4
4