
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
Лекция 8. Связность, линейная связность, компактность и отделимость топологических пространств
Из теоремы Польке – Шварца следует, что изображением тетраэдра при параллельном проектировании может служить произвольный четырехугольник (в частности и не выпуклый).
Изображением параллелепипеда, в том числе прямоугольного и куба, является фигура, состоящая из трех пар параллелепипедов, полученных друг из друга параллельным переносом.
 |
При этом строится вначале изображение тетраэдра ABDA¢. И силу теоремы Польке – Шварца оно представляет собой четырехугольник A1B1D1A1¢ плоскости изображения a. Затем этот четырехугольник достраивается до трех пар указанных параллелограммов.
Построение изображения призмы. Изображением n – угольной призмы служит фигура, состоящая из двух равных n – угольников – изображений оснований призмы, и n параллелограммов – изображений ее боковых граней. При этом построение изображений оснований подчиняется правилу построения изображения n – угольника.
Построение пирамиды. Основание n – угольной пирамиды изображается n - угольником, построение которого подчиняется правилу построения изображения n – угольника. Вершина пирамиды изображается точкой, а боковые грани – треугольниками.
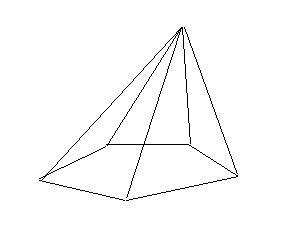
При этом из теоремы Польке – Шварца следует, что в качестве изображения вершины пирамиды и трех вершин основания можно взять произвольный четырехугольник на плоскости.
Лекция 8. Связность, линейная связность, компактность и отделимость топологических пространств.
Литература: [2] § 4, 5.
Определение 1. Пространство 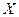 называется несвязным, если его можно представить в виде объединения двух непустых непересекающихся открытых множеств. В противном случае пространство
называется несвязным, если его можно представить в виде объединения двух непустых непересекающихся открытых множеств. В противном случае пространство 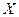 называется связным.
называется связным.
Пример 1. Пространство с дискретной топологией несвязно, а пространство с антидискретной топологией связно.
Пример 2. Пространство с топологией Зариского связно, поскольку любые два непустые открытые в нем множества имеют непустое пересечение (§1, пример 3).
Пример 3. Рассмотрим пространство  с топологией, порожденной метрикой (§1, пример 8) и докажем, что отрезок
с топологией, порожденной метрикой (§1, пример 8) и докажем, что отрезок  является его связным подпространством. Предположим, что пространство
является его связным подпространством. Предположим, что пространство 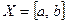 , топология которого индуцируется из
, топология которого индуцируется из  , является несвязным. Тогда найдутся такие непустые открытые в
, является несвязным. Тогда найдутся такие непустые открытые в 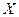 множества
множества 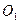 и
и 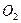 , что
, что 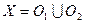 и
и 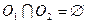 . Пусть
. Пусть 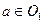 . Рассмотрим множество
. Рассмотрим множество  . Окрестность
. Окрестность 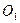 точки
точки 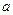 содержит ее
содержит ее 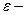 окрестность, которая в индуцированной топологии имеет вид
окрестность, которая в индуцированной топологии имеет вид  , при условии, что
, при условии, что 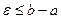 , поэтому
, поэтому 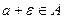 . Отсюда следует, что множество
. Отсюда следует, что множество 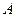 непустое. Это множество ограничено сверху точками
непустое. Это множество ограничено сверху точками 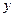 , для которых
, для которых 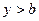 . Таким образом, множество
. Таким образом, множество 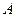 имеет точную верхнюю грань
имеет точную верхнюю грань 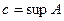 , причем
, причем 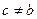 . Поскольку
. Поскольку 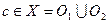 , одно из множеств
, одно из множеств 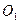 или
или 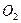 является окрестностью точки
является окрестностью точки 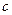 , а значит содержит ее
, а значит содержит ее 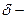 окрестность, которая имеет вид
окрестность, которая имеет вид 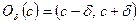 , при условии, что
, при условии, что 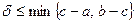 . Если
. Если 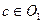 , то
, то 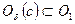 , следовательно
, следовательно  , что противоречит определению точки
, что противоречит определению точки 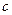 . Если
. Если 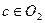 , то
, то 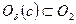 , следовательно на промежутке
, следовательно на промежутке 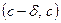 нет точек множества
нет точек множества 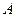 и число
и число 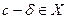 , которое меньше
, которое меньше 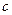 , ограничивает множество
, ограничивает множество 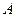 сверху, что вновь определению точки
сверху, что вновь определению точки 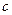 . Таким образом,
. Таким образом,  , чего не может быть. В итоге мы получили противоречие, которое показывает ложность предположения о несвязности отрезка
, чего не может быть. В итоге мы получили противоречие, которое показывает ложность предположения о несвязности отрезка 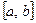 .
.
Теорема 1. Непрерывный образ связного топологического пространства является связным топологическим пространством.
Доказательство. Пусть задано непрерывное сюръективное отображение 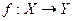 связного топологического пространства
связного топологического пространства 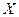 на некоторое топологическое пространство
на некоторое топологическое пространство 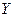 . Предположим, что пространство
. Предположим, что пространство 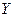 несвязно. Тогда найдутся такие непустые открытые в
несвязно. Тогда найдутся такие непустые открытые в 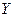 множества
множества 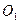 и
и 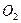 , что
, что 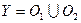 и
и 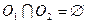 . Множества
. Множества 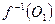 и
и 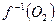 непустые, поскольку отображение
непустые, поскольку отображение 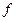 сюръективно, и открытые в
сюръективно, и открытые в 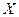 , поскольку отображение
, поскольку отображение 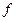 непрерывно. Кроме того,
непрерывно. Кроме того, 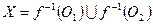 и
и 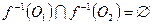 . Отсюда следует, что пространство
. Отсюда следует, что пространство 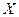 несвязно. Мы пришли к противоречию. Таким образом, пространство
несвязно. Мы пришли к противоречию. Таким образом, пространство 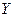 связно. Теорема доказана.
связно. Теорема доказана.
Из этой теоремы следует, что связность является топологическим свойством.
Пример 4. Пусть даны пространство 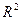 с топологией, порожденной метрикой, и окружность
с топологией, порожденной метрикой, и окружность 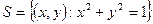 . Тогда пространство
. Тогда пространство 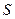 , топология которого индуцирована из
, топология которого индуцирована из 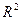 , является связным как образ отрезка
, является связным как образ отрезка 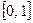 при непрерывном отображении, заданном формулами
при непрерывном отображении, заданном формулами 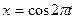 ,
,  ,
,  .
.
Теорема 2. Пространство 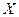 связно, если любые две его точки лежат в некотором связном подпространстве.
связно, если любые две его точки лежат в некотором связном подпространстве.
Доказательство. Предположим, что пространство 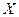 несвязно. Тогда найдутся такие непустые открытые в
несвязно. Тогда найдутся такие непустые открытые в 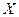 множества
множества 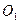 и
и 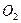 , что
, что 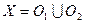 и
и 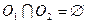 . Рассмотрим произвольно две точки
. Рассмотрим произвольно две точки 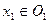 и
и 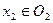 . По условию утверждения, эти точки принадлежат некоторому связному подпространству
. По условию утверждения, эти точки принадлежат некоторому связному подпространству 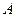 пространства
пространства 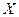 . Обозначим
. Обозначим 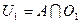 и
и  . Множества
. Множества 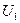 и
и 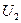 непустые и открытые в
непустые и открытые в 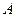 , причем
, причем 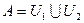 и
и 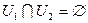 , что противоречит связности пространства
, что противоречит связности пространства 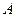 . Таким образом, пространство
. Таким образом, пространство 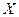 связно. Теорема доказана.
связно. Теорема доказана.
Пример 5. Пусть даны пространство 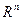 с топологией, порожденной метрикой (§1, пример 10), и выпуклое множество
с топологией, порожденной метрикой (§1, пример 10), и выпуклое множество 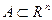 . Тогда пространство
. Тогда пространство 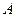 , топология которого индуцирована из
, топология которого индуцирована из 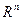 , является связным, поскольку вместе с любыми двумя своими точками выпуклое множество содержит весь отрезок с концами в этих точках.
, является связным, поскольку вместе с любыми двумя своими точками выпуклое множество содержит весь отрезок с концами в этих точках.
Определение 2. Топологическое пространство 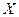 называется линейно связным, если для любых двух его точек
называется линейно связным, если для любых двух его точек 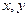 найдется такое непрерывное отображение
найдется такое непрерывное отображение 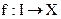 отрезка
отрезка 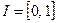 в пространство
в пространство 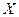 , что
, что 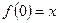 и
и 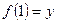 . В этом случае образ
. В этом случае образ 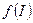 отрезка
отрезка 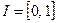 называется путем, соединяющим точки
называется путем, соединяющим точки 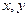 .
. 
Ясно, что путь 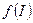 является связным подпространством пространства
является связным подпространством пространства 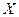 . Из теоремы 2 следует, что всякое линейно связное пространство обязательно связно. Обратное не верно, как показывает следующий пример.
. Из теоремы 2 следует, что всякое линейно связное пространство обязательно связно. Обратное не верно, как показывает следующий пример.
Пример 6. Пусть даны пространство 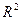 с топологией, порожденной метрикой, и множества
с топологией, порожденной метрикой, и множества 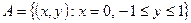 ,
, 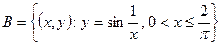 ,
, 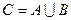 . Тогда пространство
. Тогда пространство 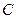 , топология которого индуцирована из
, топология которого индуцирована из 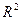 , связно, но не линейно связно, поскольку точку множества
, связно, но не линейно связно, поскольку точку множества 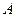 нельзя соединить путем с точкой множества
нельзя соединить путем с точкой множества 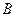 .
.
| <== предыдущая страница | | | следующая страница ==> |
| Изображение пространственных фигур при параллельном проектировании | | | Компоненты связности |
Дата добавления: 2014-08-04; просмотров: 1084; Нарушение авторских прав

Мы поможем в написании ваших работ!