
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
Компоненты связности
Если топологическое пространство не является связным, то его можно разложить на связные куски, которые и называются компонентами связности.
Теорема 3. Пусть в пространстве  для некоторого нумерующего множества
для некоторого нумерующего множества 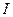 дано семейство
дано семейство 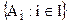 связных подпространств, пересечение которых не пусто. Тогда подпространство
связных подпространств, пересечение которых не пусто. Тогда подпространство 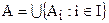 связно.
связно.
Доказательство. Предположим, что подпространство  несвязно. Тогда существуют такие непустые открытые в
несвязно. Тогда существуют такие непустые открытые в  множества
множества 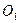 и
и 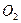 , что
, что 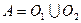 и
и 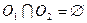 . По условию, найдется хоть одна точка
. По условию, найдется хоть одна точка 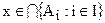 . Пусть
. Пусть 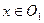 . Рассмотрим произвольно точку
. Рассмотрим произвольно точку 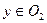 . Поскольку
. Поскольку 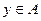 , найдется номер
, найдется номер 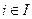 со свойством
со свойством 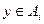 . Множества
. Множества 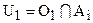 и
и 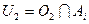 непустые и открытые в
непустые и открытые в 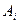 , причем
, причем 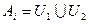 и
и 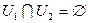 . Мы пришли к противоречию со связностью пространства
. Мы пришли к противоречию со связностью пространства 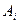 . Таким образом само пространство
. Таким образом само пространство  связно. Теорема доказана.
связно. Теорема доказана.
Пример 7. Рассмотрим пространство  с топологией, порожденной метрикой (§1, пример 8). Тогда полуинтервал
с топологией, порожденной метрикой (§1, пример 8). Тогда полуинтервал 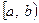 , интервал
, интервал 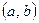 , замкнутый луч
, замкнутый луч 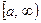 и открытый луч
и открытый луч 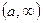 являются его связными подпространствами. Проверим, например, первое утверждение. Для каждого
являются его связными подпространствами. Проверим, например, первое утверждение. Для каждого 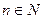 отрезок
отрезок 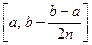 является связным подпространством, содержим точку
является связным подпространством, содержим точку 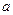 . Объединение таких отрезков по всем
. Объединение таких отрезков по всем 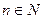 даст полуинтервал
даст полуинтервал 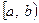 и в силу теоремы 3 этот полуинтервал связен. Аналогично можно доказать связность замкнутого луча. Далее, интервал можно представить в виде объединения двух полуинтервалов, а открытый луч – в виде объединения полуинтервала и замкнутого луча, имеющих общий конец, откуда следует их связность.
и в силу теоремы 3 этот полуинтервал связен. Аналогично можно доказать связность замкнутого луча. Далее, интервал можно представить в виде объединения двух полуинтервалов, а открытый луч – в виде объединения полуинтервала и замкнутого луча, имеющих общий конец, откуда следует их связность.
Теорема 4. Замыкание связного подпространства связно.
Доказательство. Пусть в пространстве  дано связное подпространство
дано связное подпространство  . Предположим, что замыкание
. Предположим, что замыкание 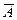 несвязно. Тогда существуют такие непустые открытые в
несвязно. Тогда существуют такие непустые открытые в 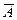 множества
множества 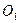 и
и 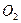 , что
, что 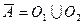 и
и 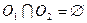 . Рассмотрим произвольно точки
. Рассмотрим произвольно точки 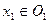 и
и 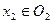 . По определению индуцированной топологии, найдутся окрестности
. По определению индуцированной топологии, найдутся окрестности 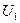 и
и 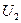 точек
точек 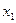 и
и 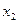 в пространстве
в пространстве  со свойством
со свойством 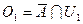 и
и 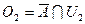 . Поскольку
. Поскольку 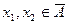 , то эти точки являются точками прикосновения множества
, то эти точки являются точками прикосновения множества  , следовательно любые их окрестности имеют со множеством
, следовательно любые их окрестности имеют со множеством  непустое пересечение. Таким образом, множества
непустое пересечение. Таким образом, множества 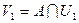 и
и 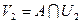 непустые и открытые в
непустые и открытые в  , причем
, причем 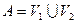 и
и 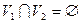 . Мы пришли к противоречию со связностью пространства
. Мы пришли к противоречию со связностью пространства  . Значит само пространство
. Значит само пространство 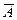 связно. Теорема доказана.
связно. Теорема доказана.
Определение 3. Для каждой точки 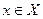 объединение
объединение 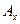 всех связных подпространств пространства
всех связных подпространств пространства  , содержащих точку
, содержащих точку 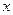 , называется компонентой связности этой точки.
, называется компонентой связности этой точки.
Из теоремы 3 следует, что подпространство 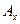 связно, а в силу теоремы 4 замыкание
связно, а в силу теоремы 4 замыкание 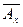 также связно. По определению компоненты связности имеем
также связно. По определению компоненты связности имеем 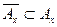 , откуда
, откуда 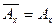 , значит множество
, значит множество 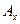 замкнуто в
замкнуто в  . Пусть
. Пусть 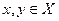 и
и 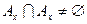 . Тогда подпространство
. Тогда подпространство 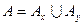 связно, поэтому
связно, поэтому 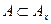 и
и 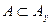 . Таким образом,
. Таким образом, 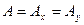 . Обратно, если
. Обратно, если 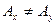 , то
, то 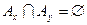 . Доказана следующая теорема:
. Доказана следующая теорема:
Теорема 5. Всякое топологическое пространство можно представить в виде объединения компонент связности замкнутых и не пересекающихся.
Можно доказать, что свойство пространств состоять из определенного числа компонент связности, понимаемого в общем случае как мощность множества, является топологическим. В случае конечного числа компонент связности, каждая из них является одновременно открытым и замкнутым множеством.
Пример 8. Рассмотрим пространство  действительных чисел с топологией, порожденной метрикой (§1, пример 8) и докажем, что в его подпространстве
действительных чисел с топологией, порожденной метрикой (§1, пример 8) и докажем, что в его подпространстве 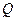 рациональных чисел компоненты связности являются одноточечными множествами. Предположим, что в пространстве
рациональных чисел компоненты связности являются одноточечными множествами. Предположим, что в пространстве 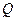 , топология которого индуцирована из
, топология которого индуцирована из  , найдется связное подпространство
, найдется связное подпространство  и две различные точки
и две различные точки 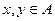 , причем
, причем 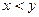 . Фиксируем такое иррациональное число
. Фиксируем такое иррациональное число 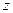 , что
, что 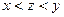 и рассмотрим два открытых луча
и рассмотрим два открытых луча 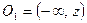 и
и 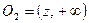 . Множества
. Множества 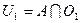 и
и  непустые и открытые в
непустые и открытые в  , причем
, причем 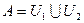 и
и 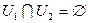 . Мы пришли к противоречию со связностью пространства
. Мы пришли к противоречию со связностью пространства  . Таким образом, пространство
. Таким образом, пространство 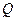 представимо виде объединения счетного числа одноточечных компонент связности, каждая из которых является замкнутым, но не открытым множеством.
представимо виде объединения счетного числа одноточечных компонент связности, каждая из которых является замкнутым, но не открытым множеством.
Хорошо известно, что многие фундаментальные факты математического анализа основаны на одном замечательном свойстве отрезка, известном под названием леммы Гейне – Бореля – Лебега и заключающемся в том, что из любого покрытия отрезка открытыми интервалами можно выбрать конечное подпокрытие. По этой причине оказалось естественным выделить класс топологических пространств, обладающих аналогичным свойством, что и привело к одному из основных понятий топологии – понятию компактного пространства.
Пусть дано топологическое пространство 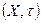 .
.
1. Понятие компактного топологического пространства.
Определение 1. Покрытием пространства  называется такое семейство
называется такое семейство  его подмножеств, объединение которого совпадает с
его подмножеств, объединение которого совпадает с  . Покрытие
. Покрытие  называется открытым, если оно состоит из открытых в
называется открытым, если оно состоит из открытых в  множеств. Подпокрытием покрытия
множеств. Подпокрытием покрытия  называется такое его подсемейство
называется такое его подсемейство 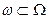 , которое само является покрытием пространства
, которое само является покрытием пространства  .
.
Определение 2. Пространство  называется компактным, если любое его открытое покрытие имеет конечное подпокрытие.
называется компактным, если любое его открытое покрытие имеет конечное подпокрытие.
Пример 1. Бесконечное множество с антидискретной топологией является ткомпакиным, а с дискретной – не является компактным пространством.
Пример 2. Бесконечное множество  , на котором задана топология Зариского (§1, пример 3) является компактным пространством. Действительно, рассмотрим произвольное открытое покрытие
, на котором задана топология Зариского (§1, пример 3) является компактным пространством. Действительно, рассмотрим произвольное открытое покрытие  пространства
пространства  и множество
и множество 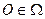 . Тогда множество
. Тогда множество 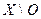 является конечным:
является конечным: 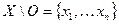 . Обозначим через
. Обозначим через 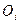 такой элемент покрытия
такой элемент покрытия  , что
, что 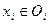 . Тогда
. Тогда 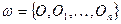 есть конечное подпокрытие покрытия
есть конечное подпокрытие покрытия  .
.
Пример 3. Рассмотрим пространство  с топологией, порожденной метрикой (§1, пример 8). Тогда полуинтервал
с топологией, порожденной метрикой (§1, пример 8). Тогда полуинтервал 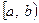 , интервал
, интервал 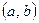 , замкнутый луч
, замкнутый луч 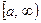 и открытый луч
и открытый луч 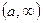 не являются, а отрезок
не являются, а отрезок 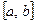 – является его компактными подпространствами. Действительно, открытое покрытие
– является его компактными подпространствами. Действительно, открытое покрытие 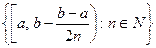 полуинтервала
полуинтервала 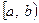 не имеет конечного подпокрытия. Аналогично можно рассуждать в случае интервала, открытого или замкнутого луча. Докажем, что пространство
не имеет конечного подпокрытия. Аналогично можно рассуждать в случае интервала, открытого или замкнутого луча. Докажем, что пространство 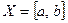 , топология которого индуцируется из
, топология которого индуцируется из  , является компактным. Рассмотрим произвольное открытое покрытие
, является компактным. Рассмотрим произвольное открытое покрытие  пространства
пространства  . Точку
. Точку 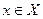 , отличную от точки
, отличную от точки 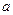 , назовем отмеченной, если отрезок
, назовем отмеченной, если отрезок 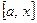 можно покрыть конечным числом множеств из
можно покрыть конечным числом множеств из  . То открытое множество из
. То открытое множество из  , которому принадлежит точка
, которому принадлежит точка 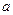 , содержит ее
, содержит ее 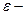 окрестность, имеющую в индуцированной топологии имеет вид
окрестность, имеющую в индуцированной топологии имеет вид  , при условии, что
, при условии, что 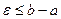 , поэтому.
, поэтому. 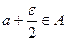 . Отсюда следует, что множество
. Отсюда следует, что множество  всех отмеченных точек непустое. Это множество ограничено сверху точками
всех отмеченных точек непустое. Это множество ограничено сверху точками 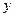 , для которых
, для которых 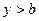 . Таким образом, множество
. Таким образом, множество  имеет точную верхнюю грань
имеет точную верхнюю грань 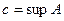 . Предположим, что
. Предположим, что 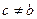 . Поскольку
. Поскольку 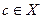 , то найдется такое множество
, то найдется такое множество 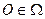 , что
, что 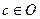 . Тогда окрестность
. Тогда окрестность 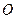 точки
точки 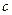 содержит ее
содержит ее 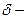 окрестность, которая имеет вид
окрестность, которая имеет вид 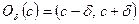 , при условии, что
, при условии, что 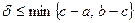 . По определению точной верхней грани
. По определению точной верхней грани 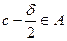 , следовательно отрезок
, следовательно отрезок 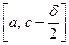 можно покрыть конечным числом элементов
можно покрыть конечным числом элементов 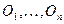 из
из  . Семейство
. Семейство 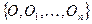 образует конечное покрытие отрезка
образует конечное покрытие отрезка 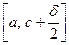 множествами из
множествами из  , так что
, так что 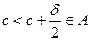 . Последнее соотношение противоречит определению точки
. Последнее соотношение противоречит определению точки 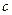 . Тем самым доказано, что
. Тем самым доказано, что 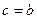 . Из определения отмеченной точки теперь вытекает существование конечного подпокрытия у покрытия
. Из определения отмеченной точки теперь вытекает существование конечного подпокрытия у покрытия  , а значит и компактность отрезка
, а значит и компактность отрезка 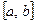 .
.
Теорема 1. Непрерывный образ компактного топологического пространства является компактным топологическим пространством.
Доказательство. Пусть задано непрерывное сюръективное отображение 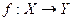 компактного топологического пространства
компактного топологического пространства  на некоторое топологическое пространство
на некоторое топологическое пространство 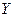 . Рассмотрим произвольное открытое покрытие
. Рассмотрим произвольное открытое покрытие  пространства
пространства 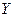 . Тогда семейство
. Тогда семейство 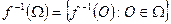 образует открытое покрытие пространства
образует открытое покрытие пространства  . Поскольку пространство
. Поскольку пространство  компактно, покрытие
компактно, покрытие 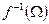 имеет конечное подпокрытие
имеет конечное подпокрытие 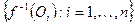 . Тогда семейство
. Тогда семейство 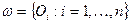 есть конечное подпокрытие покрытия
есть конечное подпокрытие покрытия  . Таким образом, пространство
. Таким образом, пространство 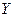 компактно. Теорема доказана.
компактно. Теорема доказана.
Из этой теоремы следует, что компактность является топологическим свойством.
Пример 4. Пусть даны пространство 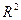 с топологией, порожденной метрикой, и окружность
с топологией, порожденной метрикой, и окружность 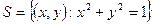 . Тогда пространство
. Тогда пространство 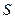 , топология которого индуцирована из
, топология которого индуцирована из 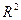 , является компактным как образ отрезка
, является компактным как образ отрезка 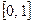 при непрерывном отображении, заданном формулами
при непрерывном отображении, заданном формулами 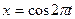 ,
,  ,
,  .
.
2. Свойства компактных топологических пространств.
Теорема 2. Всякое замкнутое множество  , лежащее в компактном топологическом пространстве
, лежащее в компактном топологическом пространстве  , есть компактное топологическое пространство.
, есть компактное топологическое пространство.
Доказательство. Рассмотрим произвольное открытое покрытие 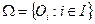 пространства
пространства  . Для любого номера
. Для любого номера  найдется такое открытое в
найдется такое открытое в  множество
множество 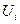 , что
, что 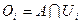 . Поскольку множество
. Поскольку множество  замкнуто, то множество
замкнуто, то множество 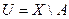 открыто в
открыто в  . Семейство
. Семейство 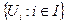 и множество
и множество 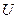 образуют открытое покрытие пространства
образуют открытое покрытие пространства  . В силу компактности пространства
. В силу компактности пространства  , это покрытие имеет конечное подпокрытие
, это покрытие имеет конечное подпокрытие 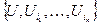 для некоторых номеров
для некоторых номеров 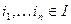 . Тогда семейство
. Тогда семейство 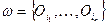 есть конечное подпокрытие покрытия
есть конечное подпокрытие покрытия  . Таким образом, пространство
. Таким образом, пространство  компактно. Теорема доказана.
компактно. Теорема доказана.
Теорема 4. Всякое бесконечное подмножество  компактного пространства
компактного пространства  имеет в
имеет в  хоть одну предельную точку.
хоть одну предельную точку.
Доказательство. Предположим противное, а именно, что производное множество 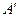 пусто. Тогда
пусто. Тогда 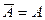 , следовательно множество
, следовательно множество  замкнуто, а множество
замкнуто, а множество 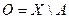 открыто в
открыто в  . Далее, для любой точки
. Далее, для любой точки 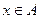 найдется в
найдется в  такая окрестность
такая окрестность 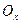 , что
, что 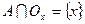 . Семейство
. Семейство 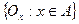 и множество
и множество 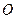 образуют открытое покрытие пространства
образуют открытое покрытие пространства  , которое не имеет конечного подпокрытия. Мы получили противоречие с компактностью пространства
, которое не имеет конечного подпокрытия. Мы получили противоречие с компактностью пространства  , которое и завершает доказательство теоремы.
, которое и завершает доказательство теоремы.
3. Компактность в метрическом пространстве.
Пусть на множестве  заданы метрика
заданы метрика 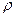 и порожденная этой метрикой топология
и порожденная этой метрикой топология 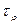 . Тогда можно рассматривать метрическое пространство
. Тогда можно рассматривать метрическое пространство 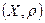 и топологическое пространство
и топологическое пространство 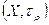 . Ниже мы получим признак компактности пространства
. Ниже мы получим признак компактности пространства  в терминах сходящихся последовательностей.
в терминах сходящихся последовательностей.
Определение 4. Метрическое пространство  называется секвенциально компактным, если каждая последовательность точек в
называется секвенциально компактным, если каждая последовательность точек в  имеет сходящуюся подпоследовательность.
имеет сходящуюся подпоследовательность.
Теорема 5. Пространство  является секвенциально компактным тогда и только тогда, когда каждое бесконечное подмножество множества
является секвенциально компактным тогда и только тогда, когда каждое бесконечное подмножество множества  имеет в
имеет в  предельную точку.
предельную точку.
Доказательство. Необходимость. Пусть пространство  является секвенциально компактным и дано бесконечное множество
является секвенциально компактным и дано бесконечное множество 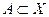 . Тогда множество
. Тогда множество  содержит счетное подмножество, элементы которого можно занумеровать в виде последовательности
содержит счетное подмножество, элементы которого можно занумеровать в виде последовательности 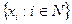 . Эта последовательность имеет подпоследовательность, сходящуюся к некоторой точке
. Эта последовательность имеет подпоследовательность, сходящуюся к некоторой точке 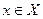 , которая и является предельной точкой множества
, которая и является предельной точкой множества  .
.
Достаточность. Пусть всякое бесконечное подмножество множества  имеет в
имеет в  предельную точку и дана последовательность
предельную точку и дана последовательность 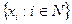 точек множества
точек множества  . Если лишь конечное множество этих точек являются попарно различными, то данная последовательность имеет сходящуюся подпоследовательность из совпадающих между собой точек. В противном случае подмножество
. Если лишь конечное множество этих точек являются попарно различными, то данная последовательность имеет сходящуюся подпоследовательность из совпадающих между собой точек. В противном случае подмножество 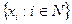 множества
множества  бесконечно, а значит имеет предельную точку
бесконечно, а значит имеет предельную точку 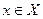 . В силу теоремы 3 из §2 эта точка является пределом некоторой подпоследовательности данной последовательности. Теорема доказана.
. В силу теоремы 3 из §2 эта точка является пределом некоторой подпоследовательности данной последовательности. Теорема доказана.
Определение 5. Число 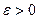 называется числом Лебега открытого покрытия
называется числом Лебега открытого покрытия  метрического пространства
метрического пространства  , если
, если 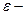 окрестность каждой точки этого пространства содержится в некотором множестве из
окрестность каждой точки этого пространства содержится в некотором множестве из  .
.
Теорема 6. Всякое открытое покрытие  секвенциально компактного пространства
секвенциально компактного пространства  имеет число Лебега.
имеет число Лебега.
Доказательство. Предположим, что покрытие  не имеет числа Лебега. Тогда для фиксированной последовательности
не имеет числа Лебега. Тогда для фиксированной последовательности 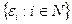 положительных действительных чисел, сходящейся к нулю, найдется такая последовательность
положительных действительных чисел, сходящейся к нулю, найдется такая последовательность 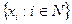 точек множества
точек множества  , что для всех
, что для всех 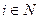 окрестность
окрестность 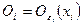 точки
точки 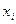 не содержится ни в одном множестве из
не содержится ни в одном множестве из  . В силу секвннциальной компактности пространства
. В силу секвннциальной компактности пространства  , можно выбрать подпоследовательность
, можно выбрать подпоследовательность 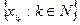 , сходящуюся к точке
, сходящуюся к точке 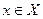 . Найдется множество
. Найдется множество 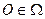 , содержащее эту точку, а значит для некоторого
, содержащее эту точку, а значит для некоторого 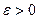 будет
будет 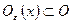 . Возьмем настолько большой номер
. Возьмем настолько большой номер 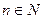 , что для всех номеров
, что для всех номеров 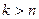 одновременно выполняются неравенства
одновременно выполняются неравенства 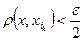 и
и 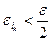 . Для любой точки
. Для любой точки 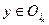 имеем
имеем 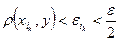 , откуда
, откуда 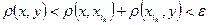 , следовательно,
, следовательно, 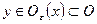 . Таким образом,
. Таким образом, 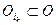 . Это включение противоречит тому, что множество
. Это включение противоречит тому, что множество 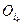 не содержится ни в одном множестве из
не содержится ни в одном множестве из  . Теорема доказана.
. Теорема доказана.
Для метрического пространства компактность и секвенциальная компактность равносильны, а именно справедлива теорема:
Теорема 7. Метрическое пространство  копактно тогда и только тогда, когда оно секвенциально компактно.
копактно тогда и только тогда, когда оно секвенциально компактно.
Доказательство. Необходимость следует из теорем 4 и 5.
Достаточность. Пусть пространство  секвенциально компактно, но существует его открытое покрытие
секвенциально компактно, но существует его открытое покрытие  , не имеющее конечного подпокрытия. Обозначим через
, не имеющее конечного подпокрытия. Обозначим через 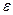 число Лебега этого покрытия и рассмотрим еще одно покрытие
число Лебега этого покрытия и рассмотрим еще одно покрытие 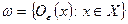 пространства
пространства  . Тогда каждое множество из
. Тогда каждое множество из  содержится в некотором множестве из
содержится в некотором множестве из  , следовательно покрытие
, следовательно покрытие  также не имеет конечного подпокрытия. Фиксируем точку
также не имеет конечного подпокрытия. Фиксируем точку 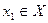 и для каждого номера
и для каждого номера 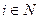 найдем точку
найдем точку 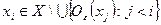 . Тем самым по индукции построена последовательность
. Тем самым по индукции построена последовательность 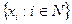 точек множества
точек множества  со свойством
со свойством 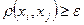 для любых
для любых 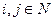 . В силу секвенциальной компактности пространства
. В силу секвенциальной компактности пространства  , можно выбрать подпоследовательность
, можно выбрать подпоследовательность 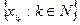 , сходящуюся к точке
, сходящуюся к точке 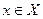 . Существует такой номер
. Существует такой номер 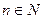 , что для всех номеров
, что для всех номеров 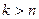 будет
будет 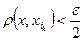 , следовательно
, следовательно 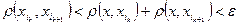 . Мы пришли к противоречию со свойством последовательности
. Мы пришли к противоречию со свойством последовательности 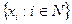 . Таким образом, всякое открытое покрытие пространства
. Таким образом, всякое открытое покрытие пространства  имеет конечное подпокрытие и само пространство
имеет конечное подпокрытие и само пространство  компактно. Теорема доказана.
компактно. Теорема доказана.
Из курса математического анализа известно, что всякое бесконечное ограниченное множество в пространстве 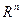 имеет хоть одну предельную точку, поэтому в качестве следствия из доказанных теорем получаем признак компактности в пространстве
имеет хоть одну предельную точку, поэтому в качестве следствия из доказанных теорем получаем признак компактности в пространстве 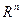 :
:
Теорема 8. Подпространство пространства 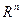 компактно тогда и только тогда, когда оно замкнуто и ограничено.
компактно тогда и только тогда, когда оно замкнуто и ограничено.
Заметим, что неограниченное подпространство не может быть компактным, поскольку из его покрытия семейством концентрических открытых шаров нельзя выделить конечного подпокрытия.
Хауздорфовость топологического пространства
Определение 3. Пространство  называется отделимым (или хаусдорфовым), если у любых двух его различных точек существуют непересекающиеся окрестности.
называется отделимым (или хаусдорфовым), если у любых двух его различных точек существуют непересекающиеся окрестности.
Пример 5. Пусть 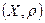 есть метрическое пространство. Тогда топологическое пространство
есть метрическое пространство. Тогда топологическое пространство 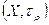 является отделимым. Действительно, если даны две различные точки
является отделимым. Действительно, если даны две различные точки 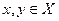 , то обозначив
, то обозначив 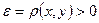 , получим, что
, получим, что 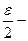 окрестности данных точек не пересекаются.
окрестности данных точек не пересекаются.
Пример 6. Пространство с дискретной топологией является, а с антидискретной – не является отделимым.
Пример 7. Пространство с топологией Зариского не является отделимым, поскольку любые два непустые открытые в нем множества имеют непустое пересечение (§1, пример 3).
Пример 8. Простое двоеточие является, а слипшееся и связное двоеточия не являются отделимыми пространствами. Пример 3 из §3 теперь показывает, что непрерывный образ отделимого пространства может не быть отделимым пространством.
Теорема 3. Пусть  есть компактное подпространство отделимого пространства
есть компактное подпространство отделимого пространства  . Тогда множество
. Тогда множество  замкнуто в
замкнуто в  .
.
Доказательство. Рассмотрим произвольно точку 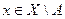 . Поскольку пространство
. Поскольку пространство  отделимо, для любой точки
отделимо, для любой точки 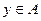 найдутся непересекающиеся окрестности
найдутся непересекающиеся окрестности 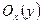 и
и 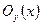 точек
точек 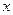 и
и 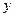 соответственно. Семейство
соответственно. Семейство 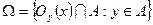 образует открытое покрытие пространства
образует открытое покрытие пространства  . В силу компактности пространства
. В силу компактности пространства  , это покрытие имеет конечное подпокрытие
, это покрытие имеет конечное подпокрытие 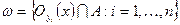 . Ясно, что множества
. Ясно, что множества 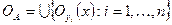 и
и 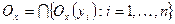 открыты в
открыты в  и не пересекаются. В частности, окрестность
и не пересекаются. В частности, окрестность 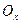 точки
точки 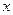 не пересекается с множеством
не пересекается с множеством  . Таким образом, множество
. Таким образом, множество  открыто, а само множество
открыто, а само множество  замкнуто в
замкнуто в  . Теорема доказана.
. Теорема доказана.
| <== предыдущая страница | | | следующая страница ==> |
| Лекция 8. Связность, линейная связность, компактность и отделимость топологических пространств | | | Гидравлические приводы |
Дата добавления: 2014-08-04; просмотров: 495; Нарушение авторских прав

Мы поможем в написании ваших работ!