
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
Изображение пространственных фигур при параллельном проектировании
Из теоремы Польке – Шварца следует, что изображением тетраэдра при параллельном проектировании может служить произвольный четырехугольник (в частности и не выпуклый).
Изображением параллелепипеда, в том числе прямоугольного и куба, является фигура, состоящая из трех пар параллелепипедов, полученных друг из друга параллельным переносом.
 |
При этом строится вначале изображение тетраэдра ABDA¢. И силу теоремы Польке – Шварца оно представляет собой четырехугольник A1B1D1A1¢ плоскости изображения a. Затем этот четырехугольник достраивается до трех пар указанных параллелограммов.
Построение изображения призмы. Изображением n – угольной призмы служит фигура, состоящая из двух равных n – угольников – изображений оснований призмы, и n параллелограммов – изображений ее боковых граней. При этом построение изображений оснований подчиняется правилу построения изображения n – угольника.
Построение пирамиды. Основание n – угольной пирамиды изображается n - угольником, построение которого подчиняется правилу построения изображения n – угольника. Вершина пирамиды изображается точкой, а боковые грани – треугольниками.
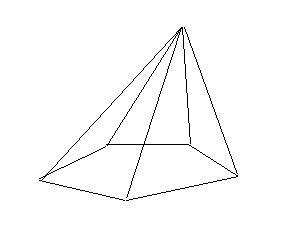
При этом из теоремы Польке – Шварца следует, что в качестве изображения вершины пирамиды и трех вершин основания можно взять произвольный четырехугольник на плоскости.
| <== предыдущая страница | | | следующая страница ==> |
| | | Лекция 8. Связность, линейная связность, компактность и отделимость топологических пространств |
Дата добавления: 2014-08-04; просмотров: 715; Нарушение авторских прав

Мы поможем в написании ваших работ!