Лекция № 3 «Касательные напряжения при изгибе. Формула Журавского. Закон распределения касательных напряжений по сечению»

Рассмотрим балку, нагруженную внешней силой Р. Возникают нормальные и касательные напряжения. При этом касательные напряжения в силу закона парности направлены от ребра к ребру.

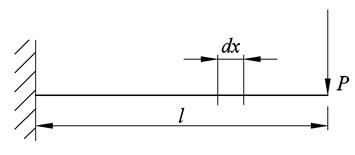
Выведем формулу для касательных напряжений. Для этого проведём через балку два вертикальных сечения на расстоянии dxдруг от друга. И ещё горизонтальное сечение на расстоянии yот нейтрального слоя.

Таким образом, из балки выделили элемент с размерами: dx, h/2-y, b.

Для составления уравнений равновесия спроецируем все действующие силы на наш элемент на ось ох.

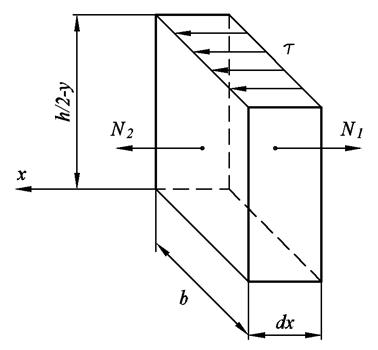
Получим, что разность нормальных усилий 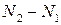уравновешивается действием касательного усилия dT.

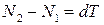
Элементарное касательное усилие dT, возникающее на площадке 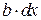будет равно:

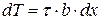
Нормальные напряжения, действующие на боковой бесконечно малой площадке dF, расположенной на уровне y от нейтральной оси, будут рассчитываться по известной формуле: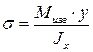

Усилие 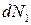, приходящееся на элементарную площадку, будет равно:

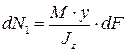
На всю боковую грань будет действовать сила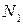

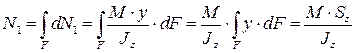
По аналогии на следующую боковую грань, выделенного элемента, действует сила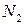

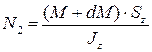
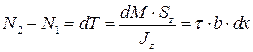
Выражая 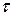, получим:

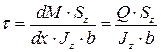- формула Журавского

Касательные напряжения, лежащие выше нейтрального слоя, прямо пропорциональны поперечной силе, статическому моменту площади фигуры, обратно пропорциональны осевому моменту инерции сечения и ширине сечения.

Выясним с помощью формулы Журавского, каким образом касательные напряжения распределяются по сечению.

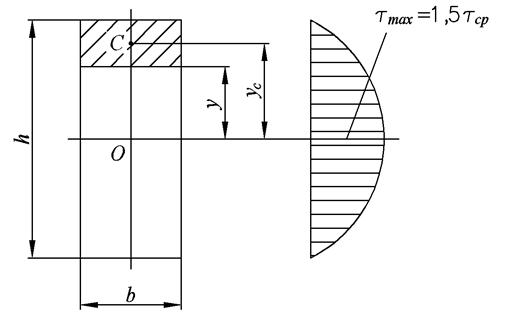
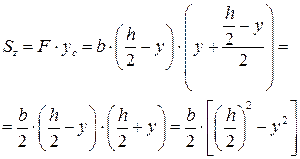
Подставим 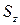в формулу Журавского, учитывая что осевой момент инерции для прямоугольного сечения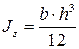

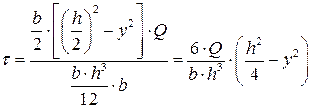
На нейтральной оси при y=0 касательные напряжения будут в полтора раза больше средних

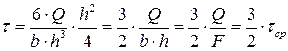
На нейтральном слое касательные напряжения принимают максимальное значение, нормальные напряжения на нейтральном слое равны нулю.

На поверхности балки касательных напряжений нет, только нормальные.

Наличие касательных напряжений несколько искажает принятую раньше схему деформации. Мы считали, что под действием изгибающих моментов поперечные сечения остаются плоскими и поворачиваются.

Под действием касательных напряжений элементы материала между двумя сечениями перекашиваются. Этот перекос в соответствии с изменением величины касательных напряжений возрастает от краев к нейтральной оси. Однако эти искривления мало отражаются на величине продольных деформациях волокон. Этот факт позволяет пользоваться формулой для нормальных напряжений

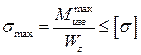
Дата добавления: 2014-03-13; просмотров: 2032; Нарушение авторских прав

Мы поможем в написании ваших работ!