Лекция № 4 «Приближённое дифференциальное уравнение упругой линии балки. Способы определения перемещений»

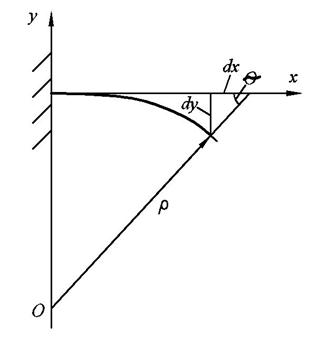
Нужно получить зависимость y – деформации от x – длины.

При получении зависимости пренебрегаем влиянием поперечной силы,

т. е. рассматриваем случай чистого изгиба.

Уже известен закон Гука при изгибе:

,

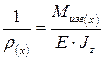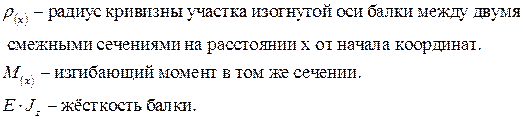
Влияние поперечной силы 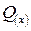на деформации невелико, поэтому ею пренебрегаем.

С другой стороны существует математическая зависимость между радиусом кривизны оси и координатами её точек х и y :

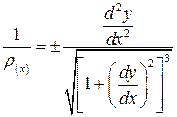
Слагаемое Очень малая величина, квадратом которой можно пренебречь. Тогда приравнивая правые части уравнений, получим:

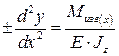
Это уравнение называется приближённым дифференциальным уравнением изогнутой оси балки.

Следует ставить знак « - » при направлении оси оy вниз,

И знак « + » при направлении оси вверх.

Условимся в дальнейшем всегда ось оy направлять вверх и дифференциальное уравнение можно переписать в следующем виде:

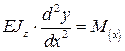
Дата добавления: 2014-03-13; просмотров: 504; Нарушение авторских прав

Мы поможем в написании ваших работ!