Лекция №2 «Нормальные напряжения при чистом изгибе. Закон Гука при изгибе. Условие прочности при изгибе»

Предисловие

Лекция № 6 «Продольный изгиб.

Лекция № 5 «Сложное напряженное состояние.

Лекция № 4 «Приближённое дифференциальное уравнение

СОДЕРЖАНИЕ

Конспект лекций. Часть 3

СОПРОТИВЛЕНИЕ МАТЕРИАЛОВ

Курзанова Е. В.

Северодвинск

УДК 539.3/8

Сопротивление материалов. Конспект лекций. Часть 3 ./Сост.

Е.В. Курзанова, Северодвинск: РИО СЕВМАШВТУЗА, 2011 г. – 56 с.

Конспект лекций часть 3 предназначен для студентов всех специальностей, изучающих курс «Сопротивление материалов».

В части 3 конспекта лекций по сопротивлению материалов содержатся основные теоретические положения и зависимости по следующим темам: «Изгиб. Основные понятия и определения», «Закон Гука при изгибе», «Касательные напряжения при изгибе. Формула Журавского», «Сложное напряжённое состояние», «Продольный изгиб», «Гипотезы прочности», «Изгиб с растяжением», «Косой пространственный изгиб», «Внецентренное сжатие», «Совместное действие изгиба и кручения».

Рецензенты:

К.т.н., доцент кафедры №3 Н.В. Лобанов,

Генеральный директор ООО «Универсал-Техно» М.В. Софрыгин.

Печатается по решению редакционно-издательского совета Севмашвтуза

© СЕВМАШВТУЗ, 2011г.

Предисловие…………………………………………………………………….4

1. Лекция № 1 «Изгиб. Основные понятия и определения»………………5

2. Лекция № 2 «Закон Гука при изгибе. Условие прочности» »..……….12

3. Лекция № 3 «Касательные напряжения при изгибе. Формула Журавского»…………………………………………………………………...16

упругой линии балки. Способы определения перемещений……………..19

Гипотезы прочности».......................................................................................31

Формула Эйлера»……………………………………………………………...36

7. Лекция №7 «Изгиб с растяжением. Косой пространственный изгиб»……………………………………………………………………………43

8. Лекция № 8 «Внецентренное сжатие»……………………………………47

9. Лекция № 9 «Совместное действие изгиба и кручения»........................49

10. Вопросы для проверки уровня знаний.....................................................53

11. Список литературы………………………………………………………..55

В части 3 конспекта лекций содержаться основные теоретические положения и расчётные формулы по следующим темам: «Изгиб. Основные понятия и определения», «Закон Гука при изгтбе», «Касательные напряжения при изгибе. Формула Журавского», «Сложное напряжённое состояние. Гипотезы прочности», «Продольный изгиб», «Изгиб с растяжением», «Косой изгиб», «Внецентренное сжатие», «Совместное действие изгиба и кручения»

Целью конспекта лекций является оказание помощи студентам при изучении предмета, при решении и защите расчетно-графических работ по сопротивлению материалов.

Конспект лекций предназначен для студентов всех специальностей, изучающих курс “Сопротивление материалов”.

Лекция №1 «Изгиб. Основные понятия и определения»

Деформация изгиба рассматривается на примере тела, имеющего простую форму. Например, брус. Брусом называется твёрдое тело, у которого длина значительно больше поперечных величин одного порядка. Ось бруса может быть кривой или прямой линией. Брусья с прямолинейной осью называются стержнями, балками, стойками, в зависимости от назначения.

Брусья с прямолинейной осью, положенные на опоры и изгибаемые приложенными к ним нагрузками (равномерно распределённая нагрузка, сосредоточенная сила, изгибающий момент) называются балками.

Балки служат для передачи действующих на них нагрузок на опоры, на которых они покоятся. Если балка имеет свешивающиеся концы, такую балку принято называть консольной, свешивающиеся концы – консолями. На опорах балки возникают реакции, с определения которых следует начинать решение всех задач, связанных с изгибом балок.

В зависимости от числа и устройства опор балки число реакций, подлежащих определению, бывает различно. Опоры балок по их устройству могут быть разделены на следующие три основных типа:

1) Шарнирно-неподвижная опора. Такая опора не даёт концу балки возможности передвигаться в каком-либо направлении, позволяя ему только поворачиваться относительно центра шарнира О. Неизвестную по величине и направлению реакцию R всегда можно заменить двумя составляющими: вертикальной R_у по оси Oy и горизонтальной R_x по оси Ox.

2) Шарнирно-подвижная опора. Такая опора отличается от шарнирно неподвижной тем, что у неё опорная подушка поставлена на катки, дающие возможность передвигаться концу балки вдоль оси по опорной плоскости. Направление опорной реакции всегда перпендикулярно к оси балки.

3) Жёстко защемляющая опора. Такая опора препятствует всякому перемещению конца балки в плоскости действия внешних нагрузок. И ещё препятствует вращению конца балки. Неизвестную реакцию R можно всегда заменить двумя составляющими: вертикальной R_у по оси Oy и горизонтальной R_х по оси Ox. И ещё неизвестный реактивный момент М_R, препятствующий повороту балки.

В практике при изгибе чаще всего силы действуют перпендикулярно к продольной оси балки. В этих случаях число неизвестных реакций, возникающих на опорах, уменьшается, так как реакция по оси Ox в шарнирно неподвижной опоре и жёстко защемляющей опоре становится равной 0.

Определение опорных реакций балок.

В случае действия на балку сил, лежащих в одной плоскости, статика даёт три уравнения равновесия:

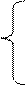
– сумма проекций всех сил, приложенных к балке, вместе с

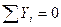реакциями опор на оси Ox и Oy равны 0.

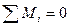– сумма моментов всех сил должная быть равна 0.

В случае действия сил перпендикулярно оси Ox уравнение обращается в тождество.

Поперечная сила и изгибающий момент.

Для определения численного значения и направления поперечной силы и изгибающего момента применяют метод сечений. Для этого нужно мысленно разрезать балку сечением перпендикулярным к горизонтальной оси, отстоящем на расстоянии x от конца балки. Отбросив ту часть балки, где действует больше нагрузок, рассматривают равновесие оставшейся части. Все внешние силы, действующие на оставшуюся часть балки, могут быть заменены парой сил и силой, действующей в сечении.

Момент М пары внутренних сил, действующий в сечении, численно равный алгебраической сумме моментов всех внешних сил, действующих на оставшуюся часть балки, называется изгибающим моментом в сечении. Всегда направлен в положительном направлении, т. е. изгибает оставшуюся часть балки выпуклостью вниз. Т. е. если часть балки левая, то 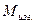вращает оставшуюся часть балки против часовой стрелки. Если часть балки правая, то 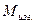вращает по часовой стрелке.

Сила Q – результирующая внутренних сил, действующая в сечении, численно равная алгебраической сумме всех внешних сил, приложенных к оставшейся части балки, называется поперечной или перерезывающей силой в сечении. Поперечную силу будем считать положительной для левой части, если она действует вниз. Для правой части считается положительной действие поперечной силы вверх.

Изгиб бруса, производимый двумя равными моментами, направленными в противоположные стороны, называется чистым изгибом. В поперечной сечении возникает только один внутренний силовой фактор – .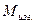

Волокна, расположенные вдоль по длине балки, растягиваются по одной стороне; по другой – сжимаются. Вследствие удлинения одних волокон на выпуклой стороне и укорочения других на вогнутой стороне, вызываемых в брусе изгибающими моментами, в поперечных сечениях бруса возникают нормальные напряжения растяжения и сжатия (направлены перпендикулярно сечению). На границе между растянутым и сжатым слоем – нейтральный слой, волокна которого не растягиваются и не сжимаются, проходящий через центр тяжести сечения.

Поперечным изгибом называется изгиб бруса, при котором в поперечном сечении возникает два внутренних силовых фактора: Q – поперечная или перерезывающая сила, 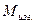– изгибающий момент. Поперечные силы вызывают касательные напряжения.

При чистом и при поперечном изгибе плоские поперечные сечения остаются плоскими и после деформации. Плоские сечения взаимно поворачиваются одно относительно другого.

В случае чистого изгиба строят эпюру изгибающего момента.

В сечении, где 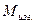имеет максимальное значение, вычисляют нормальное напряжение. Это значение напряжения сравнивают с допускаемым и делают вывод: прочность обеспечена или не обеспечена.

В случае поперечного изгиба строят эпюру изгибающего момента и перерезывающей силы. По максимальному изгибающему моменту рассчитывают нормальное напряжение.

По максимальной перерезывающей силе рассчитывают касательное напряжение. С помощью нормального и касательного напряжения находят эквивалентное нормальное по гипотезе прочности. Эквивалентное значение напряжения сравнивают с допускаемым. Делают вывод об обеспечении прочности.

Для наглядности изменения нагрузок по длине балки строят эпюры поперечной силы Q и изгибающего момента .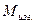

Правила построения эпюр:

Балку разбивают на участки. Проводят вниз вертикальные линии в точках приложения сосредоточенных сил и сосредоточенных моментов. Нумерация участков слева направо, если балка на двух и более опорах. Если балка со свободным концом (жесткая заделка – консоль), нумерацию следует выполнять со свободной стороны.

1. Ниже проводят две базовые нулевые линии для построения эпюры поперечной силы Q и изгибающего момента .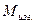

2. Положительные значения поперечной силы и изгибающего момента откладываются вверх от нулевой линии, отрицательные – вниз.

Для проверки правильности нахождения опорных реакций и определения внутренних силовых факторов Q и 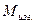, исходя из условия равновесия для оставшейся части балки, выполняют анализ эпюр.

Анализ правильности построения эпюр:

1. На участке, где нет равномерно-распределённой нагрузки, эпюра поперечной силы представляет собой прямую, параллельную нулевой оси. Эпюра изгибаюшего момента представляет собой наклонную прямую. В точке, где приложена сосредоточенная сила, на эпюре поперечной силы должен быть скачок, равный по величине сосредоточенной силе. На эпюре изгибающего момента изменяется угол наклона.

2. Если на участке есть равномерно-распределённая нагрузка, то эпюра поперечной силы представляет собой наклонную прямую. Эпюра изгибающего момента будет параболой. При действии равномерно-распределённой нагрузки вниз, значение поперечной силы на эпюре будет убывать. Эпюра изгибающего момента будет параболой выпуклостью вверх. В точке пересечении поперечной силой нулевой линии и смене знака с плюса на минус на эпюре изгибающего момента будет максимум. При действии равномерно-распределённой нагрузки вверх, значение поперечной силы на эпюре будет возрастать. Эпюра изгибающего момента будет параболой вогнутостью вниз. В точке пересечения нулевой линии и смене знака с минуса на плюс на эпюре изгибающего момента будет минимум.

3. В точке, где приложен сосредоточенный момент, на эпюре изгибающего момента должен быть скачок, равный по величине сосредоточенному моменту. На эпюре поперечной силы изменений нет.

4. При изгибе справедливы дифференциальные зависимости: 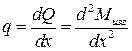- интенсивность равномерно-распределённой нагрузки рана первой производной от поперечной силы (тангенс угла наклона эпюры поперечной силы) 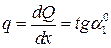и второй производной от изгибающего момента. Поперечная сила равна первой производной от изгибающего момента и равна тангенсу угла наклона касательной к кривой изгибающего момента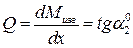

Примеры построения простейших эпюр.

Пример 1: Консоль нагружена сосредоточенным моментом, построить эпюры поперечной силы и изгибающего момента.

Эпюра поперечной силы представляет собой нулевую линию.

Эпюра изгибающего момента представляет собой линию, параллельную нулевой оси. Решение: Проведем сечение на расстоянии х от свободного, незакреплённого конца. Поперечная или перерезывающей силы 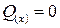так как по условию равновесия отсечённой части поперечная сила равна сумме внешних сил, действующих на отсечённую часть. Внешних сил, приложенных к конструкции нет.

Положительное направление изгибающего момента 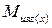, принадлежащего сечению считается направление по часовой. Изгибающий момент должен нижние волокна растягивать , верхние сжимать. В уравнении равновесия для отсечённой части он будет взят со знаком минус.

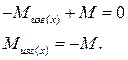
От нулевой линии откладываем вниз.

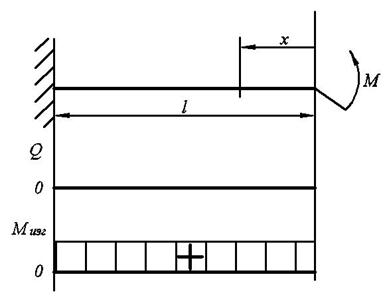
Пример 2: Консоль нагружена сосредоточенной силой, построить эпюры поперечной силы и изгибающего момента.Решение: Проведем сечение на расстоянии х от свободного, незакреплённого конца. Выберем положительное направление поперечной перерезывающей силы и изгибающего момента 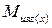. Положительным считается направление поперечной силы вверх. Так как она должна разворачивать отсечённую часть по часовой стрелке.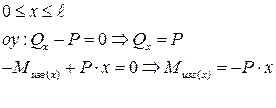Вычисляем значение изгибающего момента в граничных точках участка при х=0 и при х=l.

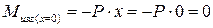
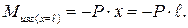
Строим эпюры поперечной силы и изгибающего момента.

Эпюра поперечной силы представляет собой линию, параллельную нулевой оси. Эпюра изгибающего момента представляет собой наклонную прямую.

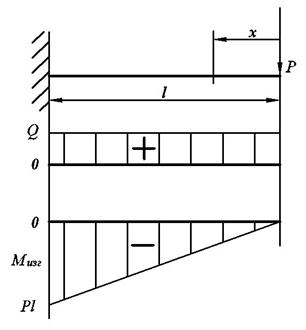
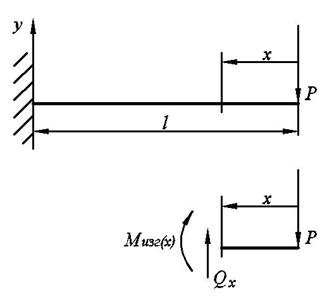
Положительное направление поперечной силы - вверх. Положительное направление изгибающего момента – по часовой стрелке. Составляем уравнение равновесия для отсечённой части в проекциях на ось ОУ для действующих сил:

Границы участка

Составляем уравнение равновесия для моментов, действующих на отсечённую часть:

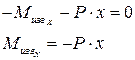
Вычисляем значение изгибающего момента в границах участка:

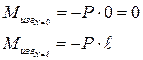
Пример 3: Балка, лежащая на двух опорах, нагружена сосредоточенной силой Р = 6Кн, построить эпюры поперечной силы и изгибающего момента.

Решение: Определяем опорные реакции в точках А и В.

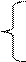SХ_i=0 – сумма проекций всех действующих сил на ось ОХ равна 0.

SМ_А=0 – сумма моментов всех сил относительно точки А равна 0 .

SМ_В=0 – сумма моментов всех сил относительно точки В равна 0 .

Проверочное уравнение:SY_i=0 – сумма проекций всех действующих сил на ось ОY равна 0.

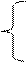SХ_i= Rвх =0

SМ_А=-2Р+6 R_ВУ =0

SМ_В=4Р - 6 R_АУ=0

R_ВУ=2 Кн

R_АУ=4 Кн

Проверка: SY_i= R_ВУ +R_АУ – Р= 2 + 4 – 6=0

Составляем уравнения для поперечной силы и изгибающего момента для каждого участка:

I участок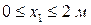

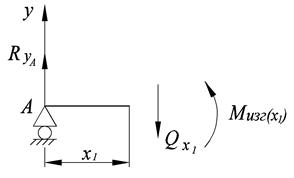
Выбираем положительное направление поперечной силы – вниз. Составляем уравнение равновесия в проекции на ось ОУ:

Выбираем положительное направление изгибающего момента – против часовой стрелки. Составляем уравнение равновесия для отсеченной части:

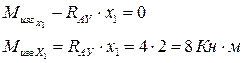
II участок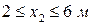

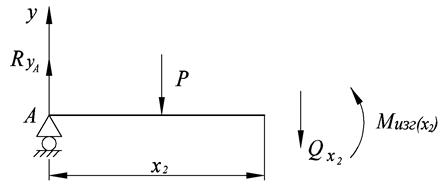
Составляем уравнение равновесия в проекции на ось ОУ для второго участка, рассматривая все силы, действующие на отсечённую часть:

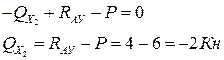
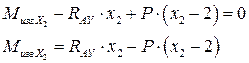
Вычисляем значение изгибающего момента в границах участка:

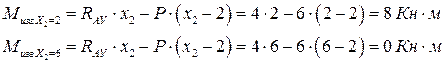
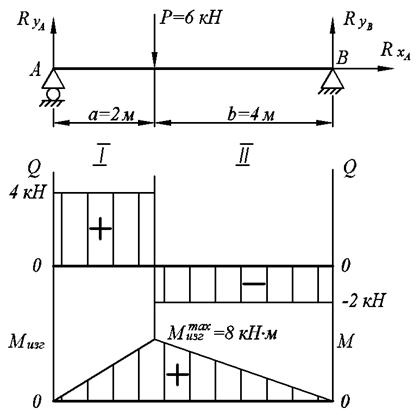
Проверка правильности построения эпюры. В точке, где приложена сосредоточенная сила, на эпюре поперечной силы должен быть скачок, равный сосредоточенной силе.

Основной метод для определения внутренних силовых факторов в сопротивлении материалов – метод сечений. Он дает возможность определить поперечную силу и изгибающий момент. Каким образом распределяются напряжения по сечению балки при изгибе? Эту задачу можно решить, рассматривая деформации. При рассмотрении деформации растяжения-сжатия было установлено, что все волокна материала получают в направлении действия сил одинаковые относительные деформации. Следовательно, нормальные напряжения при растяжении-сжатии распределяются равномерно. Установим, каким образом распределяются напряжения по сечению при чистом изгибе с помощью деформаций.

Возьмём часть балки, изгибаемую двумя равными и противоположно направленными моментами.

M N – нейтральный слой. Нейтральный слой не сжимается и не растягивается, он искривляется. Кривизной нейтрального слоя называется величина, обратная радиусу кривизны 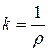, размерность 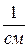,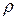- радиус кривизны.

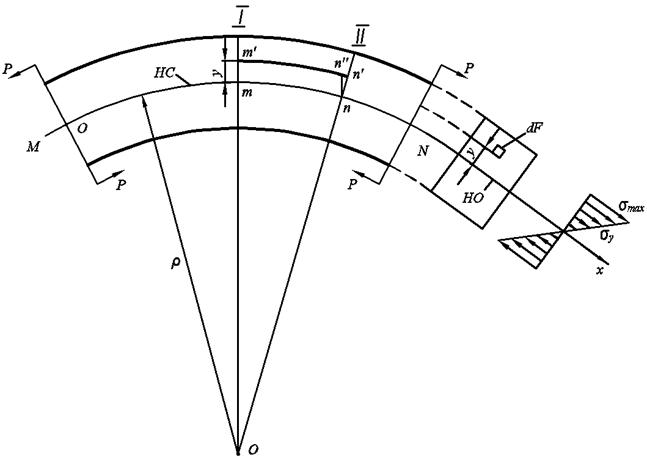
Точка О общий центр кривизны. Выделим элемент бруса между двумя сечениями (1 и 2).

Нейтральные волокна не изменили размера, а волокна на расстоянии у удлинились.

dS – длина нейтрального волокна

dS=m n=m^’ n^’’

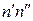- абсолютное удлинение растянутого слоя.

Из подобия треугольников и 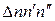можно записать следующее соотношение:

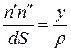
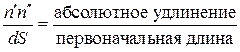-отношение абсолютного удлинения к первоначальной длине равно относительной деформации 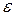, следовательно ,

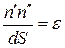это значит 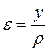- относительная деформация прямо пропорциональна расстоянию от нейтрального слоя и обратно пропорциональна радиусу кривизны.

Так как волокна бруса при изгибе испытывают только простое растяжение или сжатие, то для определения распределения напряжений по сечению можно применить закон Гука при растяжении-сжатии.

По этой формуле можно выяснить, что распределение напряжений по сечению зависит от y .

При y=0 (нейтральный слой) 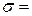0

Максимальные напряжения будут в точке, для которой расстояние y наибольшее, т. е. на поверхности балки.

При отрицательном значении y меняется знак нормальных напряжений. Нормальные напряжения будут отрицательные.

Рассчитать нормальные напряжения по формуле невозможно, так как неизвестен радиус кривизны 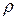. Значит нужно перейти к известным величинам, к изгибающему моменту .

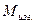dМ – элементарный момент – момент, действующий на элементарную площадку. Равный произведению элементарной нормальной силы dN на плечо y.

,

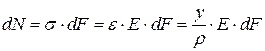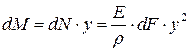
Просуммируем (проинтегрируем) все элементарные моменты dМ по всему сечению, получим 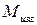, приложенный к сечению:

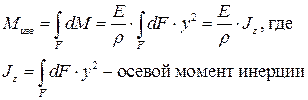
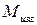- изгибающий момент, берётся максимальное значение с эпюры изгибающего момента.

Таким образом, можно определить неизвестную величину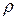

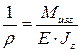- закон Гука при изгибе

Кривизна нейтрального слоя прямо пропорциональна изгибающему моменту и обратно пропорциональна произведению модуля Юнга на осевой момент инерции сечения 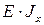- жёсткость сечения при изгибе.

Вычислим значение напряжения в любой точке сечения

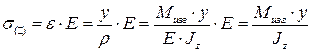
Нормальные напряжения в любой точке сечения прямо пропорциональны изгибающему моменту, расстоянию до нейтрального слоя и обратно пропорциональны осевому моменту инерции сечения.

Наибольшие нормальные напряжения на поверхности, при значении y=h/2

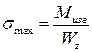
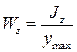- момент сопротивления изгибу.

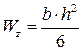- момент сопротивления изгибу для прямоугольного сечения, геометрическая характеристика балки.

Условие прочности при изгибе:

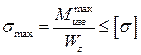
Максимальные напряжения меньше или равны допускаемым. Прочность обеспечена.

При изгибе нейтральный слой проходит через центр тяжести сечения.

Для этого рассмотрим продольную силу, действующую в любом сечении, которая по условию равновесия равна сумме внешних сил, действующих на отсечённую часть балки.

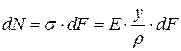
Так как все силы упругости, действующие в сечении, равны внешним, при этом сумма всех внешних сил в проекциях на ось оx равна нулю (два внешних момента, созданные из системы двух равных и противоположно направленных сил, равны и противоположно направлены).

Значит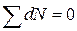

Заменим сумму на интеграл

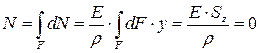
Из всех слагаемых, входящих в данную формулу только статический момент площади сечения 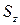может равняться нулю, когда нейтральная ось проходит через центр тяжести сечения.

Это означает, что нейтральная ось проходит через центр тяжести сечения.

Дата добавления: 2014-03-13; просмотров: 1225; Нарушение авторских прав

Мы поможем в написании ваших работ!