Интерполяционная формула для системы узких резонансов

Рассмотрим замедление в среде с поглотителем, имеющим резонансы при энергиях 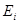. Если резонансы не перекрываются (изолированные), то вероятность поглощения нейтронов каждым из резонансов слабо зависит от наличия других резонансов, поэтому 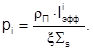. Тогда вероятность избежать резонансного поглощения при замедлении на всей совокупности резонансов

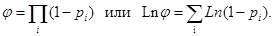
Считая 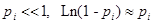, так что

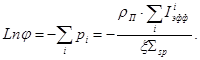(43)

Таким образом, в этом приближении эффективный резонансный интеграл 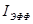оказывается аддитивной величиной и можно ввести суммарный эффективный резонансный интеграл

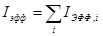(44)

причем

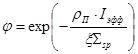. (45)

Разобьем все множество резонансов на две группы: сильные и слабые резонансы. Конечно, граница между группами достаточно неопределенна и зависит от концентрации поглотителя 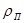. Пренебрегая этой зависимостью, получим простейшую аппроксимацию для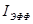

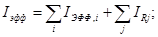(46)

где первая сумма берется по сильным резонансам ( 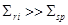), а вторая по слабым ( 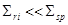). Подставляя в (46 ) выражения (26) и (40), получим

Каждая из сумм является ядерной константой для данного поглотителя, не зависящей от его концентрации резонансного поглотителя 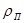. Обозначим их через b и a соответственно, тогда

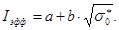
Константы a и b могут быть вычислены с помощью резонансных параметров или найдены путем обработки результатов измерений эффективного резонансного интеграла. Для ²³⁸U эта зависимость имеет вид

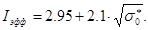
При максимальной концентрации ²³⁸U 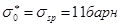, так что минимальная величина 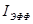=10 барн, тогда как I_R=280 барн. С разбавлением ²³⁸U замедлителем 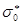и 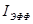растут, но при очень малых концентрациях ²³⁸U сильные резонансы становятся слабыми и полученная формула неприменима.

Дата добавления: 2014-08-09; просмотров: 474; Нарушение авторских прав

Мы поможем в написании ваших работ!