Определения и понятия, которые известны из школьного курса

Электронный образовательный ресурс

Учебно-методическое пособие к самостоятельному изучению

КУРС ЛЕКЦИЙ

«МАТЕМАТИКА (модуль 2)»

для студентов 1-го курса

отдельных разделов дисциплины «Математика»

(Для студентов всех форм обучения)

Авторы (составители):

к.т.н., доцент О.А. Алейникова

Рассмотрен и рекомендован

для использования в учебном процессе на 2012/2013 – 2017/2018 уч. г. на заседании Кафедры «Математика». Протокол № 1 от 03 09 2012 г.

Шахты 2012

1. Множество – совокупность некоторых объектов, объединённых по какому-нибудь признаку. Его объекты – элементы. Множество, не содержащее ни одного элемента, - пустое (обозначается Ø). Числовые множества:

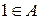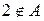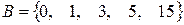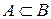, , . , , А - подмножество В.

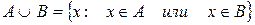- сложение.

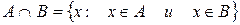- умножение.

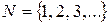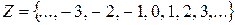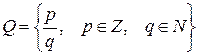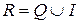, , , , I – множество иррациональных чисел, десятичных непериодических дробей.

2. Соответствие (правило) f, которое каждому элементу 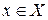сопоставляет один и только один элемент 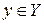, называется функцией, действующий из Х в У. 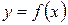. Или 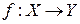. Х – область определения 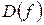. У – область значений 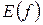. Есл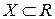и и 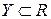, это числовая функция. х – аргумент. у – функция. Задать функцию - задать правило. Три способа: аналитический, графический и табличный.

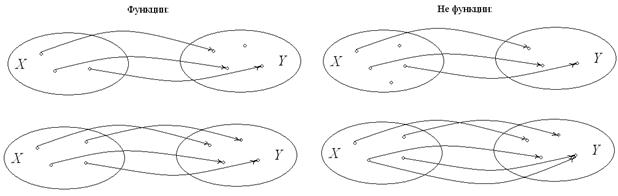
3. Если 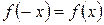- чётная. Если 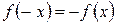- нечётная.

4. Если для любых 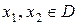из того, что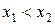

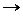
а) 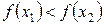, то 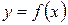- возрастающая на ;

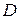б) 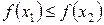, то 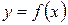- не убывающая на ;

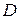в) 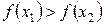, то 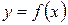- убывающая на ;

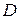г) 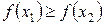, то 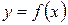- не возрастающая на ;

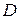Такие функции называются монотонными на 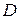. В случаях а) и в) – строго монотонными.

5. 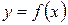называется ограниченной на 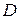, если существует число М >0, что для всех 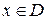выполняется 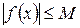. Т.е. график лежит между прямым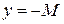и и .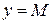

6. 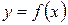называется периодической на 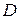, если существует число Т >0, что для всех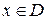 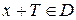и 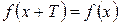. Т – период. Основной период – наименьший.

7. Если функция взаимнооднозначная, т.е. если каждому 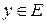соответствует единственный 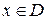, то определена 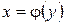с областью определения Е и множеством значений - 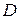. Такая функция называется обратной к . .

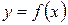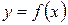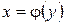и - взаимно обратные. Графики взаимно обратных функций симметричны относительно прямой .

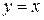Примеры.

8. Пусть 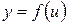определена н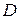а , а 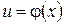, , 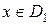причём, каждому 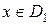соответствующее значение 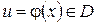. Тогда на 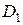определена функция 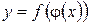, которая называется сложной функцией от 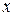( суперпозицией или функцией от функции). 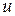- промежуточный аргумент. Сложная функция может иметь несколько промежуточных аргументов.

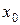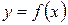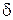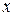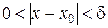
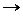
9. - точка максимума (минимума) функции , если найдётся для неё - окрестность: для любого : 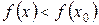(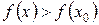). Это точки экстремума. Это не всегда наибольшее и наименьшее значения функции.

Основные элементарные функции.

1. Показательная: .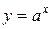

2. Степенная: (,,,,,).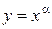

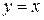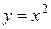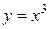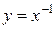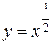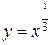3. Логарифмическая: .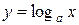

4. Тригонометрические: ,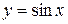

, , .

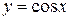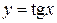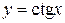5 Обратные тригонометрические: , , , .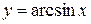

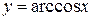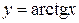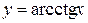Функция, задаваемая одной формулой, составленной из основных элементарных функций и постоянных, с помощью конечного числа арифметических действий и операций «функции от функции», называется элементарной функцией.

Теоремы о непрерывных функциях.

1. Всякая элементарная функция непрерывна в своей естественной области определения.

1). Многочлен 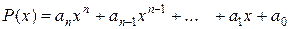непрерывен на .

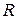2). Рациональная функция 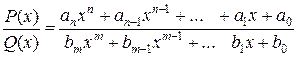непрерывна во всех точках 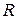кроме нулей .

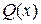3). Функции 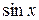, , 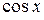, , 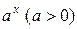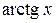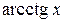непрерывны на .

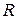4). Функция 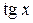непрерывна при .

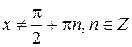5). Функция 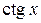непрерывна при .

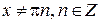6). Функции 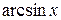, 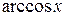непрерывны на .

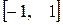7). Функции 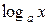, 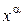непрерывны при .

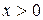Пример. Рассмотрим функцию 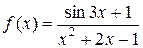. Она непрерывна в точке 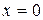, поэтому .

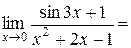
2. (Вейерштрасса) Если функция непрерывна на отрезке, то она достигает на этом отрезке своего наибольшего и наименьшего значений.

Следствие: Если функция непрерывна на отрезке, то она ограничена на нём.

3. (Больцано-Коши) Если функция непрерывна на отрезке и принимает на его концах неравные значения 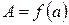и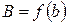, то на нём она принимает и все промежуточные значения между А и В.

Следствие: Если функция непрерывна на отрезке и принимает на его концах значения разных знаков, то внутри отрезка найдётся хотя бы одна точка, в которой данная функция обращается в нуль.

Определение. 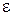– окрестностью (в дальнейшем просто окрестностью) точки 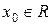называется интервал , .

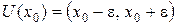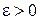Проколотая окрестность точки 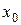– множество \.

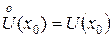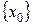Окрестность символа : .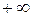

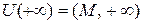Окрестность символа : .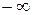

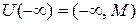Окрестность символа : .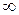

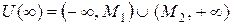Определение. Точка 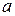(или бесконечный символ) называется точкой сгущения множества 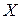, если любая окрестность точки 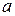содержит точки множества 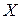, отличные от .

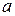Пусть функция 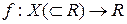и 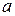– точка сгущения множества .

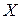Определение. Число (или бесконечный символ) А называется пределом функци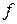и при 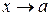, если для любой окрестности точки А найдётся проколотая окрестность 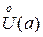точки 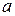такая, что 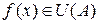для любого .

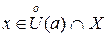Обозначение: .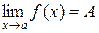

Если в определении предела функции в конечной точке а потребовать дополнительное условие 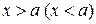, то получим определение предела справа (слева).

Обозначения: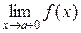, 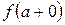– предел справа, 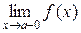, 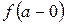– предел слева.

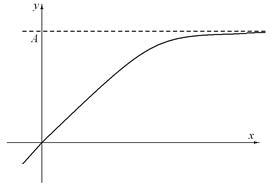
Графически 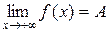можно изобразить, например, следующим образом:

Одним из примеров числовой функции может служить числовая последовательность ().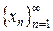

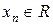Определение предела последовательности можно дать следующим образом:

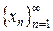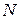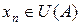Число (или бесконечный символ) А называется пределом числовой последовательности , если для любой окрестности найдётся такой номер , что для всех .

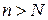Пример. Рассмотрим последовательность 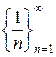и покажем, что 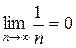. Возьмём произвольную окрестность 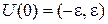точки 0 и номер 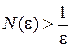. Тогда при всех 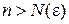будет справедливо неравенство , т.е. 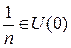при всех 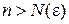. Таким образом, .

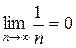Определение. Функция 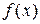называется бесконечно малой (б.м.) при 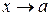, если .

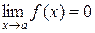Определение. Функция 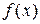называется бесконечно большой (б.б.) при 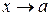, если функция 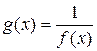является б.м. при .

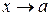Для бесконечно большой функции .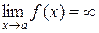

Пример. Функция 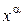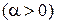при 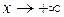является б. б., т.к. функция 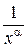– б.м. при .

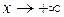Отметим некоторые основные свойства пределов функции.

1. Если существует предел функции в точке а, то он единственен.

2. Для того чтобы в точке а существовал предел функции 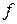, необходимо и достаточно, чтобы в этой точке у функции 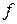существовали равные односторонние пределы справа и слева.

3. Если существуют конечные пределы 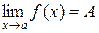, , 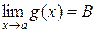то

а) ;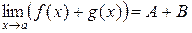

б) , ;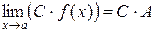

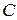
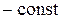в) ;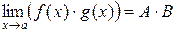

г) , .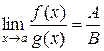

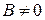4. Для того, чтобы функция 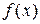имела конечный предел равный А при 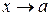, необходимо и достаточно, чтобы в некоторой проколотой окрестности точки а имело место представлени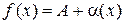е , где 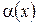– б.м. при .

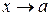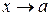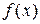5. Если – б.м. функция при , – ограниченная функция в некоторой проколотой окрестности точки а, то 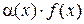– б.м. при .

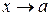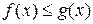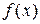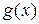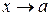6. Если в некоторой проколотой окрестности точки а выполнено неравенство и существуют пределы функций , при , то .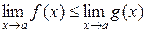

Пример. Пусть 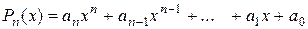– многочлен степени 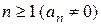. Найдем 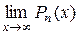. Имеем

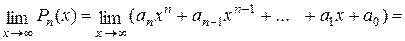
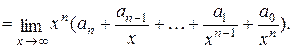
Так как 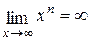и ,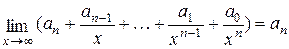

то 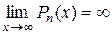. Следовательно, любой многочлен степени не ниже 1 является бесконечно большой функцией на бесконечности. Отсюда, в частности, следует, что .

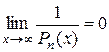Определение. Функция 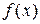называется непрерывной в точке 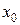, если .

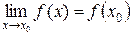Таким образом, чтобы найти предел непрерывной функции в точке 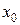, нужно вычислить значение функции в этой точке.

Если 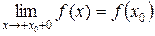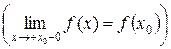, то функция 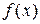называется непрерывной справа (слева) в точке .

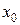Отметим некоторые свойства непрерывных функций.

1) Для того чтобы функция 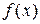была непрерывной в точке 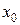, необходимо и достаточно, чтобы она была непрерывна справа и слева в этой точке.

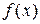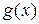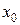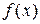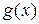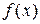
2) Если функции и непрерывны в точке , то функции +, , 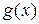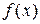/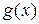(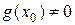) непрерывны в точке .

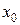3) Если функция 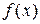непрерывна в точке 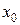, а функция 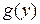непрерывна в точке 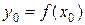, то сложная функция 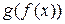непрерывна в точке .

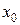Определение. Функция 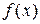называется непрерывной на множестве 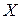, если она непрерывна в каждой точке этого множества.

Основные элементарные функции непрерывны в своей естественной области определения:

1). Многочлен 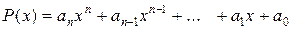непрерывен на .

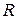2). Рациональная функция 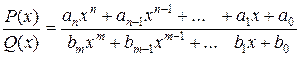непрерывна во всех точках 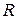кроме нулей .

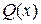3). Функции 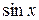, , 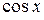, , 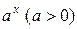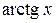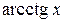непрерывны на .

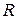4). Функция 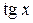непрерывна при .

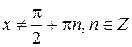5). Функция 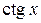непрерывна при .

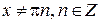6). Функции 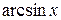, 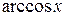непрерывны на отрезке .

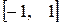7). Функции 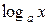, 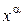непрерывны при .

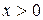Пример. Рассмотрим функцию 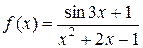. Она непрерывна в точке 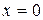, поэтому .

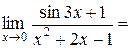
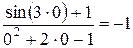Определение. Пусть функция 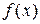определена в некоторой окрестности точки 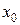, кроме, быть может, самой этой точки. Точка 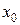называется точкой разрыва функции 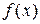, если функция 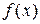не определена в точке 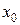или если она определена в этой точке, но не является в ней непрерывной.

Определение. Точка 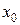называется точкой устранимого разрыва функции 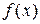, если в этой точке существует конечный предел 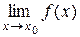, но в самой точке функция либо не определена, либо значение функции в точке 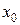не совпадает со значением предела.

Определение. Точка 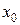называется точкой разрыва первого рода функции 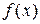, если в этой точке существуют конечные, не равные между собой односторонние пределы функции 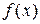. Разность 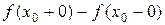называется скачком функции в точке .

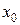Точка разрыва, не являющаяся точкой устранимого разрыва и точкой разрыва первого рода, называется точкой разрыва второго рода.

Рассмотрим некоторые пределы, которые наиболее часто используются в дальнейшем.

Определение. Предел 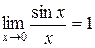называется первым замечательным пределом.

С помощью этого предела нетрудно получить некоторые следствия:

; ; .

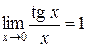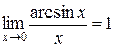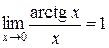Определение. Предел 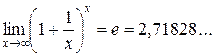называется вторым замечательным пределом.

Используя этот предел, можно получить следующие результаты:

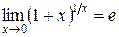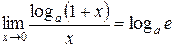; , в частности, ;

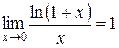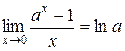, в частности, .

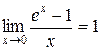При вычислении пределов часто используется эквивалентность б.м. функций.

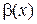Определение. Бесконечно малые функции и при 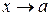называются эквивалентными, если .

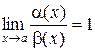Обозначение ~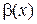при .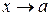

Используя первый и второй замечательные пределы и их следствия, можно составить таблицу эквивалентных бесконечно малых функций при .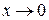

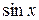~ х

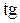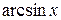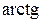х ~ х

~ х

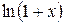х ~ х

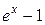~ х

~ х

Пусть и 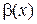эквивалентные б.м. функции при 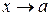и существует предел 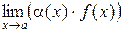. Тогда существует

=.

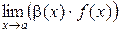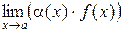Иными словами, при вычислении пределов можно заменять бесконечно малый множитель на эквивалентную ему функцию.

ПРАКТИЧЕСКАЯ ЧАСТЬ

Дата добавления: 2014-02-28; просмотров: 557; Нарушение авторских прав

Мы поможем в написании ваших работ!