Полугрупповая теория формирования базы знаний ЭС

Для конкретной компьютерной реализации учебного процесса в рамках ЭС, алгоритм обучения, представленный в табл. 4.1, следует выразить в версии подходящего языка программирования. Однако для создания интересующей ЭС этого недостаточно, т.к. входящие в модель (рис. 4.1) автоматы, по сути, являются определенными абстрактными алгебраическими конструкциями, которые для конкретного воплощения следует наполнить содержанием или, иными словами, для рассматриваемой ЭС должны быть сформированы необходимые базы знаний.

Необходимые базы знаний для ЭС, реализующей развивающее обучение в рамках рекурсии (4.1) по алгоритму табл.4.1, формируются, исходя из анализа конфигурации процесса обучения, представляющей киберсистему из двух автоматов А= (A;S;Z;f;g) иА' = (A';S';Z';f';g') с обратной связью (рис. 4.1), выраженной функциональными соотношениями (4.3), (4.4). Специфика взаимодействия автоматов такова, что Z=A'; A= Z' и S' 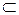S и, по сути, мы имеем дело с алгеброй (A;S;Z;f;g;f';g'), определенной на множествах A,S,Z посредством четырех бинарных операций f;g;f';g' в виде функций (4.3), (4.4). Таким образом, формирование базы знаний для интересующей ЭС связано с наполнением предметным содержанием данной алгебры и эта процедура представляется следующей.

Пусть в рамках указанной алгебры описывается предметное обучение от некоторого актуального уровня развития S' до уровня S, при котором происходит «освоение» зоны потенциального развития 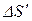обучаемого субъекта: S= 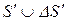. В этом случае освоение 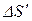осуществляется с помощью соответствующей системы вопросов и заданий, задаваемой обучаемому, которая представляет собой определенное конечное множество Z, формируемое на основе экспертных данных, так, что 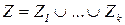, где Z_i – система вопросов i-го, i= 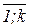эксперта. Формально Z_i – это некоторое частично упорядоченное множество в виде семантической сети, источники которой задают вопросы, инициирующие рассматриваемый процесс обучения, и, в целом, такие вопросы выделяются в отдельное подмножество 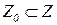. Тогда стоки – это вопросы, связанные с финальной стадией этого процесса. Аналогично, по экспертным данным, исходя из запросов множества Z, моделируется множество А ответов обучаемого субъекта, представляющее объединение экспертных оценок .

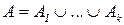Дальнейшими действиями, между множествами А и Z устанавливаются бинарные отношения 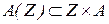и 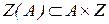, с помощью которых формируется реляционная база знаний, представляющая таблицы соответствий: между вопросами базы Z и ответами базы А, так, что с парой 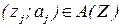связан определенный уровень знаний S 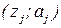, отвечающий условию 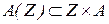: 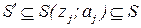, (4.5)

и, между ответом базы А и последующим вопросом базы Z так, что с парой 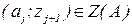связан определенный уровень знаний S 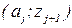, отвечающий условию 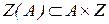: 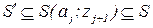. (4.6)

В результате выстраивается реляционная база знаний для множества состояний S=A(Z) 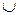Z(A), в рамках которой определяются функции f;g;f';g' и, таким образом, алгебра (A;S;Z;f;g;f';g') наполняется содержанием, реализуя ЭС для отработки методов развивающего обучения.

Процедура обучения в рамках описанной базы знаний алгебры (A;S;Z;f;g;f';g') формально выражается следующим образом. На множестве состояний S=A(Z) 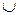Z(A), как на алфавите, задается конечная частично упорядоченная полугруппа, описывающая процедуру обучения в виде композиции: (z₀; a₀) (a₀; z₁) (z₁; a₁) … (a_e-1; z_e) (z_e; a_e), (4.7)

где z₀ 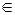Z₀, z₁; … ; z_e 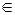Z, a₁; … ; a_e 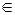A, e-ограниченный натуральный параметр, указывающий количество вопросов-ответов, содержащихся в некоторой экспертной стратегии ведения учебного процесса, связанного с освоением заданной зоны потенциального развития 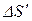. Поскольку количество композиций конечной длины вида (4.7) над конечным алфавитом S также конечно, то для каждой такой композиции можно определить рейтинг и, таким образом, сравнивать эффективности соответствующих стратегий обучения, что позволяет проводить оптимизацию учебного процесса в рамках рассматриваемой ЭС. Для введения таких рейтингов следует определить меру на множестве всех всевозможных стратегий вида (4.7). По аналогии с известным принципом наименьшего действия, можно, например, положить, что из двух стратегий (4.7) более предпочтительна та, для которой параметр e меньше, поскольку в этом случае требуется освоение меньшего количества информации (по А.Н. Колмогорову [8]). При этом стратегии, имеющие одинаковые значения параметра e, сводятся в классы эквивалентности и называются равносильными (или эквивалентными) стратегиями. Тогда, определив минимум параметра e на множестве стратегий (4.7), для данного учебного процесса определяется множество оптимальных стратегий со значением 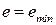и каждой такой стратегии присваивается рейтинг, например, 100%. Проводя далее ранжировку стратегий по возрастанию параметра e, с помощью величины 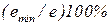определяются рейтинги стратегий (4.7).

Таким образом, можно говорить о разработке математической модели обучающей ЭС, реализующей учебный процесс в диалоге на основе концепции развивающего обучения Л.С. Выготского, которая включает:

1). Алгоритм развивающего обучения, представленного в структуре диалоговой модели в виде композиции алгебраических автоматов и операции обратной связи (п.4.2);

2). Процедуру формирования и пополнения соответствующих баз знаний ЭС и их представление в виде семантической сети или гипертекста;

3). Построение и отработку учебных стратегий развивающего обучения путем прокладки и оптимизации учебных траекторий по элементам баз знаний реализуемой ЭС.

В рамках данного математического описания в архитектуре предлагаемой ЭС легко предусматриваются всевозможные help-функции (режим подсказки), что позволяет проводить обучение (тренинг) на различных уровнях подачи изучаемого материала, адаптированного для каждого обучающегося. Например, при обучении на уровне приобретения знаний режим подсказки предоставляется на всем протяжении учебного процесса, после чего, переходя на уровень консультации, обучаемый запрашивает помощь только по отдельным моментам проведения данного учебного процесса и, наконец, на уровне контроля знаний (тестирования) режим подсказки исключается. Результаты контроля знаний позволяют формировать канал селекции и типизации трудностей изучаемого материала, который представляет важный элемент данного учебного процесса, реализуя канал обратной связи.

В целом, обучение в рамках данной ЭС следует рассматривать как некоторую организационную форму учебного процесса, проводимого с использованием вполне определенной информационной технологии в виде компьютерной программы, которая может запускаться как индивидуально (на отдельном компьютере или ноутбуке), так и в локальной сети (компьютерном классе) с ведущим компьютером (сервером) или в Интернете в случае дистанционного обучения. Таким образом, в рамках данной информационной технологии обучения легко организуются как самостоятельная, так и групповая работа учащихся.

Дата добавления: 2014-10-28; просмотров: 372; Нарушение авторских прав

Мы поможем в написании ваших работ!