
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
Формализация алгоритма обучения в диалоге
При формализованном описании процесса обучения в диалоге учитель-ученик используется модель в виде киберсистемы, состоящей из двух конечных автоматов Аи А' (п.1.3), в которой автомат А= (A;S;Z;f;g) представляет управляющую систему, моделирующую действия учителя, а автомат А' = (A';S';Z';f';g'), где S' 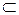 S – является управляемой системой, моделирующей поведение ученика в процессе диалога с учителем (рис.4.1).
S – является управляемой системой, моделирующей поведение ученика в процессе диалога с учителем (рис.4.1).
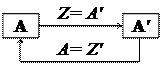
Рис. 4.1
Процесс обучения в данной модели описывается следующим образом. Выходная информация Z автомата А представляет множество вопросов, формирующих управляющее воздействие, которое задает входной массив информации A' для автомата А', так, что Z=A' и мы имеем функции переходов, соответственно,
f:S 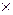 A
A 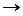 S; f':S
S; f':S 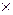 Z
Z 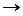 S, (4.3)
S, (4.3)
где A; S – соответственно, входная информация и множество состояний, содержащие изучаемый предметный материал, транспортируемый в процессе обучения от системы А к объекту А', обладающему подмножеством состояний S'=  в виде предметного материала, известного А' до начала процесса обучения.
в виде предметного материала, известного А' до начала процесса обучения.
Множество Z следует считать частично упорядоченным, поскольку задаваемые вопросы подчинены определенной логической стратегии, и, таким образом, выделяется класс Z0 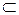 Z, содержащий минимальные элементы частично упорядоченного множества Z и, представляющий те вопросы, которыми инициируется моделируемый процесс обучения в диалоге. Если выбран исходный вопрос z0
Z, содержащий минимальные элементы частично упорядоченного множества Z и, представляющий те вопросы, которыми инициируется моделируемый процесс обучения в диалоге. Если выбран исходный вопрос z0 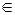 Z0 , который поставлен перед А', то, тем самым, формально происходит запуск этого процесса.
Z0 , который поставлен перед А', то, тем самым, формально происходит запуск этого процесса.
Дальнейший сценарий развивается следующим образом. Поступив на вход A' автомата А' вопрос z0 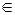 Z = A' «обдумывается» учеником, после чего принимается резолюция
Z = A' «обдумывается» учеником, после чего принимается резолюция 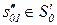 , которая позволяет перейти к состоянию с более высоким уровнем знаний
, которая позволяет перейти к состоянию с более высоким уровнем знаний 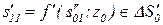 в зоне потенциального развития уровня
в зоне потенциального развития уровня 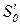 и сформулировать ответ
и сформулировать ответ 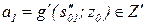 , который по каналу обратной связи (рис. 4.1) поступает на вход A управляющей системы А, так, что
, который по каналу обратной связи (рис. 4.1) поступает на вход A управляющей системы А, так, что 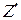 =A и мы имеем функции выходов, соответственно,
=A и мы имеем функции выходов, соответственно,
g: S 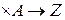 ;
; 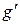 : S
: S 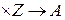 . (4.4)
. (4.4)
Поступив на вход А автомата А ответ 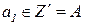 анализируется учителем, после чего принимается некоторая резолюция s11
анализируется учителем, после чего принимается некоторая резолюция s11 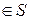 , которая переводит А в состояние s12=
, которая переводит А в состояние s12= 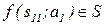 и формулирует следующий вопрос z1=
и формулирует следующий вопрос z1= 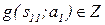 , после чего описанный процесс повторяется. Таким образом, автомат А последовательно реализует «обучение» А' с уровня
, после чего описанный процесс повторяется. Таким образом, автомат А последовательно реализует «обучение» А' с уровня 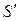 до уровня S по схеме (4.1), и затем отдается команда о прекращении данного процесса. Формальное описание этого процесса в виде алгоритма представлено в таблице 4.1, где ri – количество вопросов, которое задается учителем при
до уровня S по схеме (4.1), и затем отдается команда о прекращении данного процесса. Формальное описание этого процесса в виде алгоритма представлено в таблице 4.1, где ri – количество вопросов, которое задается учителем при
обучении на уровне 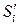 при активации зоны потенциального развития
при активации зоны потенциального развития 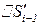 актуального уровня
актуального уровня 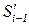 ,
, 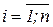 ;
; 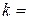 r1+r2+…+rn-1; zj – j-ый вопрос в процессе обучения, j=
r1+r2+…+rn-1; zj – j-ый вопрос в процессе обучения, j=  ;
; 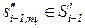
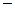 резолюция по вопросу zj, mi=
резолюция по вопросу zj, mi= 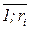 ;
; 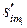 =
= 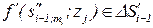 ;
; 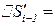 {
{ 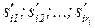 };aj+1=
};aj+1= 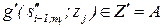
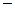 ответ на вопрос zj; sj+1;1
ответ на вопрос zj; sj+1;1 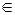 S – резолюция по ответу aj+1;
S – резолюция по ответу aj+1; 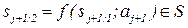 ;
; 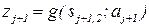
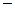 формулировка вопроса в контексте ответа aj+1;
формулировка вопроса в контексте ответа aj+1; 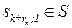 –резолюция на завершение опроса;
–резолюция на завершение опроса; 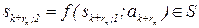
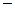 команда на остановку процесса обучения с уровня
команда на остановку процесса обучения с уровня 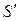 до S.
до S.
Таблица 4.1. Формальное описание алгоритма процесса обучения в диалоге учитель-ученик
| Автомат А(учитель) | Автомат А'(ученик) | Уровень обучения | ||||||
| A | Резолюция | S | Z= 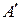
| Резолюция | S | 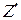
| ||
| - | - | - | z0 | 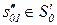
| 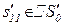
| a1 | 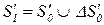
| |
| a1 | 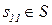
| 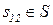
| z1 | 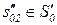
| 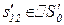
| a2 | ||
| a2 | 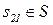
| 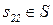
| z2 | 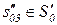
| 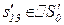
| a3 | ||
| . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . | ||||||||
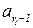
| 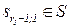
| 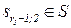
| 
| 
| 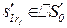
| 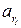
| ||
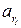
| 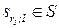
| 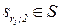
| 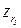
| 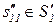
| 
| 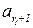
| 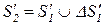
| |
| . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . | ||||||||
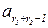
| 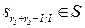
| 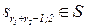
| 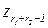
| 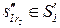
| 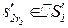
| 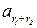
| ||
| . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . | ||||||||
| ak | 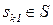
| 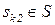
| zk | 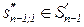
| 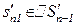
| ak+1 | 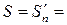 =
= 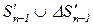
| |
| . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . | ||||||||
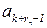
| 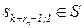
| 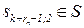
| 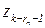
| 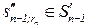
| 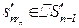
| 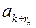
| ||
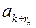
| 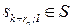
| 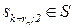
| - | - | - | - | ||
Представленная кибернетическая модель обучения в диалоге, хотя и является достаточно хорошим приближением к реальности, однако полной адекватности в этой модели не достигается, если учесть ряд обстоятельств:
1). В реальной ситуации уже на первом шаге диалога учитель реализует некоторый выбор исходного вопроса z0 среди других возможных представителей класса Z0 и, далее, на выбранный вопрос z0 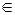 Z0 ученик дает некоторый ответ a1
Z0 ученик дает некоторый ответ a1 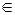
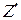 , который, если следовать традиционной шкале, может оказаться плохим, удовлетворительным, хорошим или отличным. С учетом результата a1
, который, если следовать традиционной шкале, может оказаться плохим, удовлетворительным, хорошим или отличным. С учетом результата a1 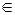 A учитель ставит вопрос z1, опять же, из некоторого класса Z1 и получает ответ a2
A учитель ставит вопрос z1, опять же, из некоторого класса Z1 и получает ответ a2 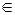
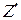 и т.д. Следовательно, в реальности функции переходов f;
и т.д. Следовательно, в реальности функции переходов f; 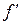 и функции выходов g;
и функции выходов g; 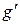 автоматов А и А' – это случайные процессы, а сценарий в табл. 4.1 – одна из возможных реализаций процесса обучения. Поэтому процесс обучения в диалоге учитель-ученик с позиций кибернетики описывается киберсистемой из двух конечных стохастических автоматов.
автоматов А и А' – это случайные процессы, а сценарий в табл. 4.1 – одна из возможных реализаций процесса обучения. Поэтому процесс обучения в диалоге учитель-ученик с позиций кибернетики описывается киберсистемой из двух конечных стохастических автоматов.
2). Поскольку каждое новое состояние обозначенной киберсистемы зависит только от ее предыдущего состояния, то поведение данной системы описывается некоторым марковским процессом с конечным множеством состояний. Такие киберсистемы можно представлять в виде семантических сетей [5;6], где пропускные способности между элементами сети определяются вероятностями переходов между соответствующими состояниями системы в данном марковском процессе [7]. В данной интерпретации на сетях можно рассматривать задачи оптимизации, имея в виду, например, эффективное (развивающее) обучение в диалоге.
| <== предыдущая страница | | | следующая страница ==> |
| Психологические аспекты обучения в диалоге | | | Полугрупповая теория формирования базы знаний ЭС |
Дата добавления: 2014-10-28; просмотров: 284; Нарушение авторских прав

Мы поможем в написании ваших работ!