Общие сведения о математических моделях

Лекция 14. Математические модели объектов проектирования

Тема.3. Математические модели обьектов проектирования

Математическое моделирование – это процесс создания модели и оперирование ею с целью получения сведений о реальном объекте.

Альтернативой математическому моделированию является физическое

макетирование. Но у математического моделирования есть ряд преимуществ:

1) меньшие сроки на подготовку анализа;

2) значительно меньшая материалоемкость, особенно при проек-

тировании крупногабаритных объектов;

3) возможность выполнения экспериментов на критических ре-

жимах, которые привели бы к разрушению физического макета;

4) удобство работы с математической моделью;

5) возможность моделирования любого процесса (там, где выполнить физическое макетирование невозможно).

Математической моделью называют совокупность математических объектов (чисел, символов, множеств и т.д.) и связей между ними, отражающих важнейшие для проектировщика свойства проектируемого технического объекта. Это свойства систем, элементов систем и внешней среды. Количественные выражения этих свойств называются параметрами. Различают выходные (Y), внутренние (X) и внешние (Q) параметры.

Y = (y1, y2, y3, ... , ym), где m количество выходных параметров;

X = (x1, x2, x3, ... , xn), где n количество внутренних параметров;

Q = (q1, q2, q3, ... , ql), где l количество внешних параметров.

Эти параметры связаны функциональной зависимостью Y =F(X, Q).

К математическим моделям предъявляются требования универсальности, адекватности, точности и экономичности.

Степень универсальности характеризует полноту отображения в модели свойств реального объекта. Математическая модель отображает лишь некоторые свойства объекта. Как правило, физические и информационные процессы и не касается других. Например: геометрические формы (резистор).

Точность математической модели оценивается степенью совпадения значений параметров реального объекта и значений параметров, рассчитанных с помощью MM. Относительная погрешность

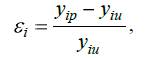
где yip расчетные выходные параметры,

yiu истинные выходные параметры.

Вектор погрешности имеет вид 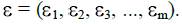. Один из вариантов оценки погрешности по максимальному значению

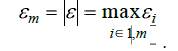
Адекватность математической модели это способность отображать заданные свойства объекта с погрешностью не выше заданной.

Адекватность имеет место обычно в ограниченной области изменения внешних переменных области адекватности.

Экономичность математической модели характеризуется затратами вычислительных ресурсов (затратами машинного времени (Тм) и памяти (Пм) на ее реализацию). Чем меньше Тм и Пм, тем MM экономичнее. Эти параметры зависят и от ЭВМ.

Иногда используют другие величины: размерность системы уравнений, количество операций выполняемых за одно обращение к модели и др.

Требование экономичности противоречит первым трем, поэтому при удовлетворении этих требований необходим компромисс.

Процесс математического моделирования можно разделить на 4 этапа:

1. Формулирование законов, связывающих основные объекты модели. Этот этап требует широкого знания фактов, относящихся к изучаемым явлениям и глубокого проникновения в их взаимосвязи. Эта стадия завершается записью в математических терминах сформулированных качественных представлений о связях между объектами модели.

2. Исследование математических задач, к которым приводят математические модели. Основным вопросом здесь является решение прямой задачи, а именно, получение в результате анализа модели выходных данных для дальнейшего их сопоставления с результатами наблюдений изучаемых явлений. На этом этапе важную роль приобретает

математический аппарат, необходимый для анализа математической модели, и вычислительная техника как мощное средство для получения количественной выходной информации в результате решения сложных математических задач.

3. Выяснение того, удовлетворяет ли принятая гипотетическая модель критерию практики, то есть выяснения вопроса о том, согласуются ли результаты наблюдений с теоретическими следствиями модели в пределах точности наблюдений.

4. Последующий анализ модели в связи с накоплением данных об изучаемых явлениях и модернизация модели.

Метод математического моделирования, сводящий исследование явлений внешнего мира к математическим задачам, занимает ведущее место среди других методов исследования, особенно в связи с появлением ЭВМ. Он позволяет проектировать новые технические средства, работающие в оптимальных режимах, для решения сложных задач науки и техники.

Дата добавления: 2014-02-26; просмотров: 613; Нарушение авторских прав

Мы поможем в написании ваших работ!