Аналитико-экспериментальный метод формализации математических моделей принятия оптимальных решений

Разработанные и предложенные в предыдущих разделах данной главы методы формализации различных математических моделей требуют значительных дополнительных исследований для их практического использования. Проблема заключается в необходимости вывода аналитического вида целевых функций, условий и ограничений, определяющих формализуемую модель. В некоторых случаях (чаще всего при решении классических задач оптимизации) эти выражения можно получить из теоретических соображений. Однако, для ряда практических многокритериальных задач принятия решений такой подход не всегда приемлем. Поэтому в данном разделе предложен метод формализации математических моделей принятия решений использующий аналитико-экспериментальный подход.

На втором этапе реализуется алгоритм процедур, представленный на рисунке 3.3, обеспечивающих формализацию оптимизационной математической модели принятия решений.

Согласно представленному алгоритму, прежде всего, следует определить критерии оптимизационной задачи, по которым будут оцениваться полученные результаты (блок 1). В качестве таких критериев выбрано подмножество переменных, обозначенное . Блок 2 обозначает процедуру выбора подмножеств независимых переменных 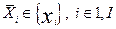, и зависимых переменных 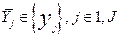, которые совместно с независимыми переменными полно и однозначно описывают исследуемый процесс. В рамках выполнения данной процедуры определяются пределы изменения независимых переменных, 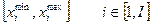, а также пределы изменения зависимых переменных .

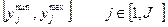Затем выбирается подмножество постоянных величин 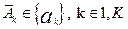, которые считаются известными для решаемой задачи (блок 3).

С учетом введенных выше обозначений формализация задачи оптимизации параметров производственных процессов будет осуществляться в виде (3.10).

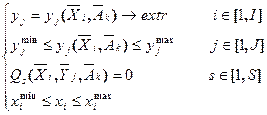(3.10)

Первая строчка выражения формализует достижение экстремальных значений критериями задачи. Вторая и четвёртая строчки формализуют ограничения, накладываемые на значения критериев и значения независимых переменных. Третья строчка формализует s условий, которым должны удовлетворять переменные параметры задачи.

Дальнейшая задача сводится к формализации неизвестных зависимосте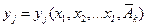й и 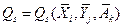. Эта процедура обозначены блоком 4, включающим составные элементы 4.1 – 4.9. Искомые зависимости можно формализовать исходя из следующего предположения. В большинстве случаях мы можем экспериментально измерить те значения, которые принимают критерии задачи в зависимости от тех или иных значений, которые мы можем задать независимым переменным. Если задавать из ОДЗ некоторые упорядоченные значения i – томунезависимому переменному, сохраняя при этом некоторые постоянные значения остальным переменным то можно (используя специальные методы), установить аналитические выражения зависимости j-го критерия от i-той переменной для заданных постоянных значений остальных переменных.

Таких аналитических зависимостей j-го критерия от i-той переменной можно построить M вариантов, где M ровно количеству сочетаний значений остальных переменных, которые мы будем задавать в порядке эксперимента. Задав для выбранного варианта с номером m, некоторое фиксированное значение 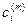всем остальным переменным и изменяя значение параметра 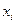в пределах от до 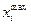с интервалом 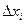, равным пределу точности измерений, можно измерить и внести в таблицу значения величины .

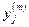Таблица 3.1

				…
				…	…

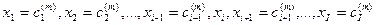
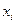
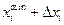
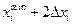
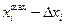
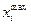
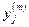
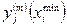
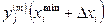
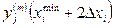
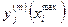
По данным, проведённым в таблице 3.1, можно установить с помощью методов компьютерной математики аналитическое выражение функции

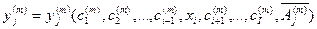, (3.11)

где 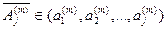- постоянные числовые коэффициенты, характеризующие установленную зависимость. Введем следующее обозначение.

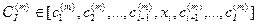. Отметим, что подмножество числовых коэффициентов 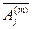, в самом общем случае зависит от .

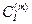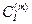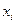Используя свой эвристический интуитивный опыт, инженер-исследователь, во многих практических случаях, сможет подобрать ограниченное число вариантов подмножеств , которые позволят ему достаточно полно и однозначно характеризовать зависимость критерия от переменной и установить аналитическое выражение (3.11).

Такую процедуру следует повторять для всех I 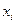переменных. В результате мы установим I аналитических зависимостей j-го критерия от всех I переменных.

Следует отметить важный вывод. Зависимость j -го критерия от некоторых переменных может быть установлена теоретически. Это целесообразно делать для тех случаев, когда эксперимент по каким-либо причинам не может быть проведён.

Затем, используя I аналитических выражений зависимости j-го критерия от каждой 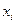переменной, инженер-исследователь может построить один или несколько вариантов аналитического выражения j-го критерия (j-ой целевой функции) от всех 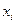переменных. Одним из способов такого построения является представление критерия в виде произведения установленных функций одной переменной.

Последующие процедуры (блок 4) направлены на то, чтобы численно оценить полученное аналитическое выражение j-го критерия на точность описания им проведённых экспериментальных исследований. Это можно сделать, рассчитав относительное среднеквадратичное отклонение экспериментальных значений критерия от их аналитических значений.

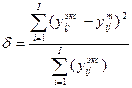(3.12)

где 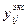и 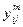- i-е значение j-го критерия, полученное, соответственно, экспериментальным и теоретическим путём.

В данном выражении буквой I обозначено число экспериментальных точек при измерении зависимости по 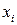-той переменной (блоки 4.1 - 4.6).

§3.7 Формализация математических моделей свойств объектов, процессов и явлений в виде дифференциальных уравнений первого порядка.

На практике в некоторых случаях модель исследуемого процесса удается записать в виде аналитической зависимости, характеристик процесса и явления от других переменных и вычисленных параметров. Такой вид формализации соответствует описанному в параграфе 3.3 частному случаю модели 3.1.

Часть переменных и других сложно построенных моделей (например , ряд моделей) могут быть построены на основе дифференциальных уравнений, в виде интегральных уравнений. В этом случае, если возникает необходимость в самостоятельном составлении моделей некоторого процесса, следует предварительно установить, каким законом подчинен исследуемый процесс и какими математическими выражениями его следует описывать.

Решение многих технических задач связано с необходимостью составления уравнений трех типов (вышеназванных). Дифференциальные уравнения получаются, когда для элементов составляемого процесса устанавливают соотношение между функцией и переменными. Применением такой задачи может служить определение давления воды на плотине, определение работы выкаченной жидкости из резервуара.

Дифференциальные уравнения производных применяют для тех случаев, когда исследуемые процессы характеризуются скоростью их изменения (диффузий, химических реакций). Представим наиболее распространенные случаи возможных процессов и явлений, описываемых их дифференциальными уравнения, и общий вид функций, которая является решением уравнений.

Наиболее распространенные виды дифференциальных уравнений первого порядка и их решения:

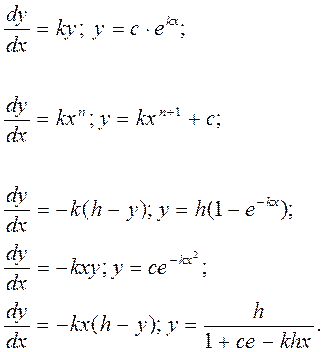
Основные стадии создания математических моделей с использованием дифференциальных уравнений первого порядка.

На первой стадии процесс мысленно разбивается на элементарные акты. Протяженность каждого, из которых выбирается такой, чтобы можно было допустить линейность соотношений между приращениями функций.

На второй – Подробно разрабатываются условия задачи, и составляется чертеж, наиболее полно отражающий поставленную цель.

На третьей – Составляются соотношения между переменными приращений для элементарного акта процесса.

На четвертой – Производиться написание дифференциального уравнения рассматриваемого процесса в целом.

На пятой – Находятся общие решения дифференциального уравнения путем интегрирования.

На шестой – Исследуется полученное решение.

На седьмой - Определяются вспомогательные параметры (коэффициент пропорциональности и др.) на основании допустимых условий задачи.

На восьмой – Формализация рассмотренного процесса и числовое определение искомых величин из формул.

На девятой – Анализируется получаемый результат и проверяется на соответствие с исходными данными.

При составлении модели, таким образом, следует выделять только те процессы, которые влияют на поставленную цель. Не следует при составлении модели стремиться учесть все многообразие процессов в исследуемом объекте, так как это ведет к чрезмерному усложнению задачи.

§3.8 Формализация математических моделей свойств объектов, процессов и явлений в виде дифференциальных уравнений второго порядка.

В задачах явления движения твердых частиц, влажных материалов в потоке газовой сушилки, а также в решении задач определения сопротивления деформациям материала, определяют закон движения рабочего органа.

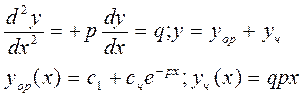
где 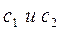находятся из граничных условий задачи. Моделирование производится на основе математической физики: с помощью уравнений математической физики, решая задачу, устанавливается закономерности движения воды, тепла, распределения давления в массиве, устанавливается закономерность в процессе переработки пород. Общее уравнение переноса субстанции (массы, энергии, и т.д.) имеет вид:

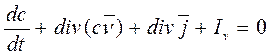
где с - концентрация субстанций как функции времени t и координат (x,y,z):

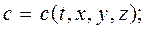
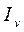- количество субстанций, выделившихся или поглощенных, в единице объема.

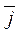- плотность молекул потока.

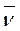- вектор скорости переноса конвективным путем.

Распространено также уравнение вязкой жидкости:

где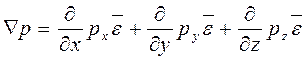

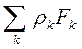- сумма действующих внешних сил.

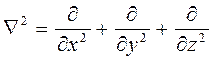
Построение моделей с использованием уравнением математической физики. В общем случае уравнение второго порядка математической физики записывается в виде:

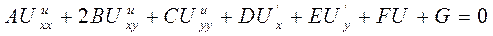
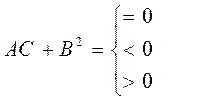
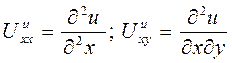
A, B, C, D, E, F, G – постоянные числа, коэффициенты.

Различают три типа уравнений второго порядка:

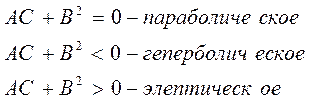
Простым примером параболического уравнения является уравнение теплопроводности:

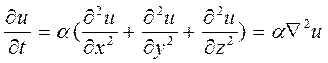
Глава 3 Математические методы оптимизации в компьютерных моделях принятия решений.

Оптимизация – выбор решения, обеспечивающий наилучший результат функционирования системы.

Постановка задачи оптимизации начинается с выявления цели.

Критерий оценки достижения поставленной цели называют показателем эффективности или критерием оптимальности.

Целевая функция – это функциональная зависимость критерия

оптимальности от не зависимых параметров задачи.

Дата добавления: 2014-08-04; просмотров: 735; Нарушение авторских прав

Мы поможем в написании ваших работ!