
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
Классификация основных математических методов оптимизации
В данной главе проанализированы основные математические методы, которые используются для построения оптимизационных математических моделей, применяемых в компьютерных системах поиска оптимальных технических решений производственных задач. Ядром оптимизационных компьютерных моделей является оптимизационная математическая задача, включающая метод ее численной реализации. Важным аспектом построения компьютерной модели является ее проверка на адекватность и достоверность.
Как было указано в предыдущей главе, современные компьютерные методы принятия решений базируются на теории принятия решений и теории исследования операций. В свою очередь, теория исследования операций использует ряд специальных математических методов, которые называют методами теории исследования операций. Вместе с тем современный математический аппарат, используемый для построения компьютерных моделей принятия решений значительно шире, нежели методы теории исследования операций. Методы компьютерной математики, современные численные методы, использующие специальные пакеты прикладных программ, методы имитационного моделирования успешно могут использоваться для построения компьютерных моделей. Безусловно, они используются наряду с такими методами, как исследование функций на экстремум с использованием дифференциального исчисления, вариационными методами, методами множителей Лагранжа, методами линейного и динамического программирования, теория игр, сетевые методы, методами статистическими методами , методами прогнозирования, и другими методами.
В данной главе, на основе анализа практического использования вышеперечисленных математических методов, предпринята попытка представить в сжатой форме необходимые сведения о наиболее используемых из них при построении компьютерных моделей принятия решений. Другими словами, предпринята попытка представить необходимые минимальные сведения о наиболее часто используемых математических методах, для практического использования их при построении компьютерных систем принятия решений предназначенных для повышения эффективности производства.
Из анализа доступной по данному вопросу информации можно заключить, что основными аналитическими методами оптимизации, используемыми в моделях производственных процессов, являются:
- исследование функций на экстремум;
- метод множителей Лагранжа;
- метод вариационного исчисления;
- методы линейного программирования;
- методы динамического программирования;
- теория игр;
- сетевые методы;
- статистического анализа и прогнозирования.
Одним из наиболее известных подходов поиска оптимальных значений параметров моделей являются методы, основанные на исследовании функций на экстремум. К ним относятся:
- методы на основе теории дифференциальных и интегральных исчислений;
- методы вариационного исчисления;
- методы множителей Лагранжа;
- градиентные методы.
Как уже указывалось выше, ряд специальных математических методов использует теория исследования операций. К этим методам, иногда называемым методами теории исследования операций, относятся:
- экономическо-математическое моделирование;
- математическое программирование;
- теория статистического анализа;
- теория массового обслуживания;
- теория игр;
- теория графов.
В свою очередь, математическое программирование включает:
- целочисленное программирование;
- линейное программирование;
- нелинейное программирование;
- динамическое программирование
Теория статистического анализа включает:
- корреляционный анализ;
- регрессионный анализ.
Следует отметить, что все разделы математики, применяемые для решения задач моделирования и обоснования принимаемых решений, в конечном итоге служат для поиска оптимальных решений. Поэтому теория дифференциальных уравнений, включающая линейные и нелинейные дифференциальные уравнения, методы математической физики, векторная алгебра и аналитическая геометрия, а также другие разделы математики имеют важнейшее значение для решения прикладных оптимизационных задач. Кроме того, графические методы оптимизации, включающие графоаналитические методы, а также методы основанные на использовании автоматизированных систем проектирования и управления производством находят в настоящее время широкое применение при решении задач оптимизации производственных процессов.
В следующих параграфах данной главы предпринята попытка исследования различных методов оптимизации применительно к решению задач оптимизации параметров производственных процессов.
§3.2 Оптимизации параметров производственных процессов на основе метода Лагранжа и методов вариационного исчисления.
В случае, если в задаче необходимо определить экстремум функции Z(x,y) при наличии ограничений типа f(x,y), применяют метод Лагранжа. Задачу называют задачей на условный экстремум.
Суть метода состоит в том, что вводится в рассмотрение функция  , где
, где 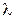 - множитель Лагранжа.
- множитель Лагранжа.
Координаты оптимальной точки 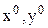 и параметр
и параметр 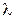 находятся из системы уравнений:
находятся из системы уравнений:
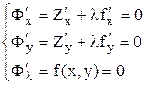
Характер экстремума определяется соотношениями:
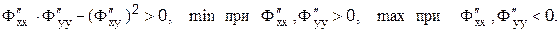
В тех случаях, когда требуется найти систему функций 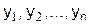 , реализующую экстремум функционала
, реализующую экстремум функционала
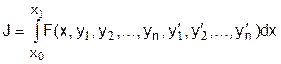
совместно с условиями вида 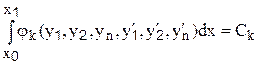
(Ск- заданные постоянные), для гладких функций 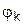 также применим метод Лагранжа.
также применим метод Лагранжа.
Для такого случая строится функция 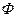 в виде
в виде
 .
.
В этом случае неизвестные функции 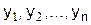 и множители Лагранжа
и множители Лагранжа  находятся из системы уравнений.
находятся из системы уравнений.
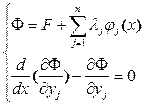 С помощью метода множителей Лагранжа легко решаются задачи выбора кратчайшего маршрута трассы магистрального канала, распределения сырья между параллельно работающими установками (прессами), обоснования формы и размеров поперечного сечения каналов прессов и многие другие.
С помощью метода множителей Лагранжа легко решаются задачи выбора кратчайшего маршрута трассы магистрального канала, распределения сырья между параллельно работающими установками (прессами), обоснования формы и размеров поперечного сечения каналов прессов и многие другие.
Этот метод может быть использован при определении оптимальной формы и размеров различных геометрических объектов (бункеров, гранул, отвалов, профилей различных сооружений и т.д.), при распределении сырья, продукции между параллельно работающими конвейерами и в других задачах.
Вариационное исчисление применяется во многих задачах механики. Например, при определении моментов инерции, центра тяжести, уравнения траектории, поверхности, площади поверхности вращения и других. Многие задачи механики и физики в целом сводятся к утверждению, что функционал в рассматриваемом процессе должен достигать максимума или минимума. Эти законы носят название вариационных принципов механики. К числу вариационных принципов принадлежат: принцип наименьшего действия, законы сохранения энергии, импульса, принцип Кастилиано в теории упругости и другие.
Таким образом, предметом вариационного исчисления является отыскание неизвестных функции 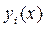 реализующее мах или мин функционалов вида:
реализующее мах или мин функционалов вида:
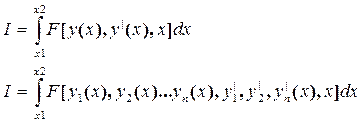
Пределы интегрирования х1 и х2 известны, а также известны граничные значения искомой функции у(х).
В теории вариационного исчисления показано, что в случае «одномерной» задачи необходимым условием существования экстремума функционала I. служит уравнение Эйлера 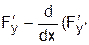 )=0. Экстремаль y(x), найденная из уравнения Эйлера, должна удовлетворять граничным условиям.
)=0. Экстремаль y(x), найденная из уравнения Эйлера, должна удовлетворять граничным условиям.
В том случае, когда функционал зависит от n- функций, то каждая из функций 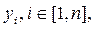 обеспечивающая экстремум функционала удовлетворяет системе уравнений Эйлера, а именно:
обеспечивающая экстремум функционала удовлетворяет системе уравнений Эйлера, а именно:
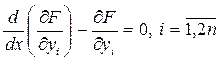
Функции 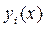 , удовлетворяющие системе уравнений Эйлера называются экстремалями решаемой задачи.
, удовлетворяющие системе уравнений Эйлера называются экстремалями решаемой задачи.
Характер экстремума функционала определяется условиями Лежандра. Функция имеет min, если 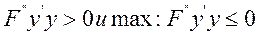
Если функция в подынтегральном выражении содержит производные более высокого порядка 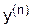 :
:
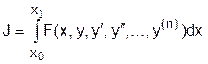
с граничными условиями
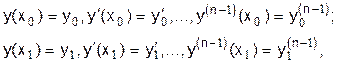
то уравнение Эйлера принимает вид:
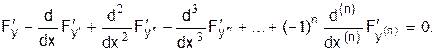
| <== предыдущая страница | | | следующая страница ==> |
| Аналитико-экспериментальный метод формализации математических моделей принятия оптимальных решений | | | Оптимизация параметров производства с использованием методов линейного и динамического программирования |
Дата добавления: 2014-08-04; просмотров: 453; Нарушение авторских прав

Мы поможем в написании ваших работ!