Оптимизация параметров производства с использованием методов линейного и динамического программирования

Модель линейного программирования представляет собой совокупность линейных алгебраических уравнений и неравенств, выражающих функции цели и их ограничения.

Математическая модель линейного программирования представляет собой выражение:

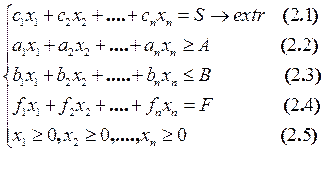
Решение задач тип (2.1-2.5) составляет предмет линейного программирования. В случае двух переменных, задача линейного программирования может быть решена геометрическим методом (например):

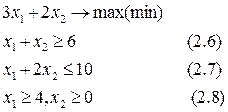
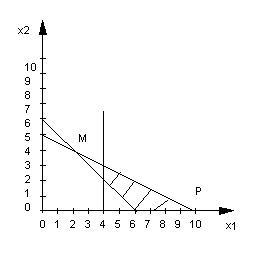Исходя из ограничений (2.6-2.8) построим область допустимых значений: Тогда область допустимых значений представляет собой заштрихованную фигуру. Построить прямую 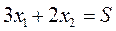где S которая величина, которую надо найти. Минимальное значение ее будет достигнуто в точке «М», а максимальное – «Р».

Симплекс метод решения задач линейного программирования может быть формализован следующим образом.

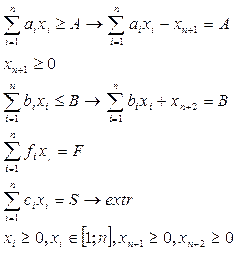
Если мы имеем n переменных и 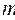уравнений - ограничений, то все 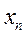решений могут быть произвольным образом разбиты на 2 группы. К первой группе отнесем т. н. базисные решения - х₁,х₂,…,х_m ( всего m решений). Ко второй группе отнесем оставшиеся 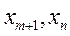решений (их всего n-m ). Эти решения, будем считать, могут принимать произвольные значения. Они, как правило, называются свободными решениями. Для такого случая все 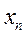решений могут быть получены, как совокупность свободных решений и базисных. Базисные решения могут быть выражены через свободные решения, и соответственно будут зависимыми от них.

Исходя из вышеизложенного, преобразуем задачу линейного программирования к виду (2.9 – 2.12).

Предположим, что мы ищем решение, обеспечивающее min S. Если, при этом в выражении 2.9 все 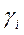больше нуля, то приняв в качестве свободных решений нулевое значение, получим, что минимальным значением S будет

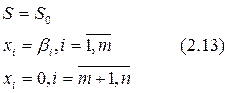
В задачах на S max следует таким образом выбрать подмножество базисных решений, чтобы в результате преобразования задачи линейного программирования к виду (2.9 – 2.12) все значения 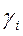были отрицательными. Для обоих случаев решение (2.13) можно считать оптимальным. В том случае, если в задаче ищется минимальное значение величины S , а один или несколько коэффициентов 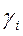отрицательны и, наоборот, положительны в задаче на S max, то следует по определенному алгоритму заменить один или несколько элементов подмножества, представляющее базисное решение на элементы из подмножества свободных решений.

Метод динамического программирования применяется для нахождения оптимальных решений в многошаговых, многоэтапных задачах. Многоэтапная задача может решаться одним из двух способов. Первый заключается в формировании множества всевозможных вариантов развития процесса и выбора из них наилучшего.

S

B

C

F

A

0 i U_i

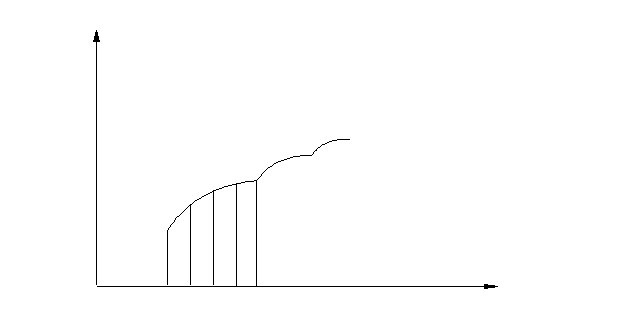
Он является более трудоемким, однако позволяет получить наглядным способом оптимальное решение, удовлетворяющее заданным критериям. При наличии современных вычислительных средств, этот способ, по мнению автора, является более предпочтительным и, вполне, реализуемым на практике. Второй способ заключается в пошаговой оптимизации многоэтапного процесса, когда состояние процесса на i +1- ом этапе оптимизируется исходя из его состояния на i – том этапе.

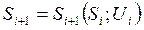, где 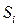- функция, характеризующая состояние процесса на i – том этапе, а 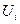- функция, характеризующая управляющее воздействие на процесс на этом же этапе. Предполагается, что суммарный, например, экономический эффект, полученный от перемещения системы из состояния А в состояние В равен сумме экономических эффектов, полученных на каждом i-том этапе при перемещении объекта.

Величина критерия оптимальности, развития объекта (процесса) описывается суммированием значений:

.

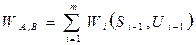Этот способ построения решения назван методом динамического программирования. В его основу положен принцип оптимальности, суть которого состоит в следующем: если путь развития AFCB является оптимальным среди других возможных путей, то оптимальным будет являться также любая часть этого пути, в т.ч. и часть СВ.

Очевидно, что в интересах оптимального развития объекта, управление на каждом этапе 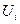должно приниматься с учётом будущего этапа, а последний этап можно планировать так, чтобы система пришла в состояние В.

На последнем этапе нужно планировать управляющее воздействие так, чтобы он сопровождался с наибольшим успехом, т.е. критерий эффективности обращался в максимум или минимум. При этом точка С может быть выбрана сколь угодно близко к конечной точке, т.е. последний этап может быть сколь угодно малым. Поэтому можно оптимальным образом спланировать этот этап, затем к этому этапу пристраивается предпоследний этап FC, к которому в свою очередь присоединяется предыдущий этап. Так можно поступать и далее всё время, увеличивая конечный отрезок пути, пока им не будет охвачен весь путь.

Метод динамического программирования может быть записан в виде рекурентного соотношения:

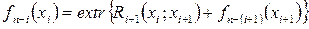2.13а

где 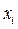, состояние системы на 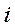–том шаге. Оно может быть представлено в виде набора параметров 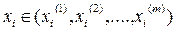. ( 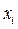по смыслу совпадает с ).

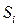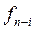– оптимальное значение эффекта, достигаемого за ( 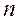- 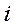) шагов.

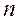– число шагов.

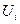- управляющее воздействие, переводящее систему из состояния из 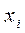в состояние 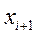(состояние системы на 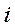+1–ом шаге).

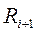– эффект, достигаемый на 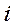–том шаге за счет перехода системы из состояния 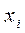в .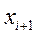

Алгоритм решения задачи методом динамического программирования может быть представлен в следующем виде.

· Записать, согласно выражению 2.13а, функциональное уравнение для последнего состояния процесса (i=n – 1)

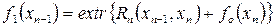
· Найти 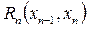из дискретного набора его возможных значений, при некоторых фиксированных 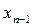, 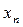. Чаще всего 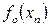принимаем равным 0, поэтому 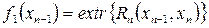. В результате первого шага найдено управляющее воздействие (решение) 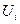, переводящее систему из состояния 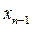в 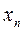и оптимальное значение эффекта, достигнутого на этом шаге .

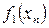· Уменьшим значение 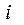на 1 и запишем для этого этапа, согласно выражения 2.13а, соответствующее уравнение и определим управляющее воздействие (решение) 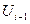, переводящее систему из состояния 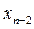в .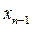

· Далее необходимо перейти к выполнению пункта 3, если не пройдены все этапы оптимизируемого процесса.

· После того, как все этапы оптимизации пройдены, необходимо снова пройти все эти этапы оптимизации, на этот раз, двигаясь от начала к концу.Этот второй расчет по этапам, по понятным причинам, будет гораздо проще первого.

Дата добавления: 2014-08-04; просмотров: 418; Нарушение авторских прав

Мы поможем в написании ваших работ!